Elektronik

19 Operationsverstärkerschaltungen

Prof. Dr. Jörg Vollrath

18 Übung

Video der 18. Vorlesung 9.12.2020

Länge: 01:26:24

0:0:10 Eine aufgebaute Operationsverstärkerschaltung

0:1:57 Oszilloskopbild

0:3:9 Verstärkungsberechnung

0:4:4 Niedrigere Frequenz hohe Verstärkung, Ausgang wird begrenzt auf Vesorgungsspannung

0:7:54 Frequenzgang eines Operationsverstärkers

0:8:54 Phasendrehung

0:10:28 Netzwerkanalysator mit Bodediagramm

0:15:12 Eckfrequenz, 3dB Frequenz

0:20:13 Gegenkopplung

0:24:59 Ua=Ue/(1/v+k)

0:28:19 Beschalteter Operationsverstärker, nichtinvertierender Verstärker

0:32:9 Impedanzwandler

0:34:37 Invertierender Verstärker

0:38:49 v = -R2/R1

0:42:14 Frequenzgang des rückgekoppelten Verstärkers

0:45:34 Frequenzgang Erläuterungen

0:48:35 20 dB/Dekade

0:50:35 vD0 = 10^(ADo/20)

0:52:58 3 dB = 20 log wurzel(2)

0:57:9 Frequenzgang mit Beschaltung

0:59:40 fg2 = 1 MHz, GBW = vu * fg2 = 1 * ft = vd0 * fg

1:2:7 Addierer

1:4:55 Knotengleichung, ohmsches Gesetz

1:8:56 Subtrahierer

1:11:16 Rechnung

1:14:13 Ansatz: (Ue1-Ux)/R1 = (Ua-Ux)/RN

1:22:31 Umformung

Rückblick und Heute

Übung
Diode, MOSFET, Operationsverstärker

Heute:
Gegenkopplung
Nichtinvertierender Verstärker
Invertierender Verstärker
Addierer
Subtrahierer
Praktischer Aufbau und Messung

Reinhold Kap. 12 S.227 - 232
Jaeger: Chap. 10 S.529-,

Gegenkopplung

Operationsverstärker: Externe Beschaltung
Gegenkopplung:

$u_D = u_e -k \cdot u_a$

Mitkopplung

$u_D = u_e + k \cdot u_a$

Koppelfaktor k
Übertragungsfunktion

$v = \infty$
k < 1

System bestimmt durch das Rückkopplungsnetz

R: linearer Verstärker
RC: aktives Filter

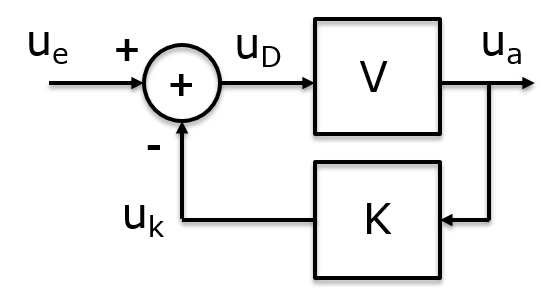$u_a = v \left( u_e - k \cdot u_a \right)$

$u_a \left( 1 + v \cdot k \right) = v \cdot u_e$

$\frac{u_a}{u_e} = \frac{v}{1+v \cdot k} = \frac{1}{\frac{1}{v}+ k}$

$V_{Ges} = \frac{u_a}{u_e} \approx \frac{1}{k}$

Grundschaltung: Nichtinvertierender Verstärker

Vergleich mit Gegenkopplung
$v$ : Verstärkung, Op $\rightarrow \infty$
k: Gegenkopplung, $k = \frac{R_2}{R_1 + R_2} < 1$
$V_{Ges} = \frac{u_a}{u_e} \approx \frac{1}{k} = \frac{R_1 + R_2}{R_2} > 1$
Spannungsverstärkung wird durch externe Elemente bestimmt.
Sonderfall

$R_1 = 0$ , $R_2 = \infty$
Spannungsfolger
Die gesamte "common mode range" wird beim Betrieb genutzt.

LTSPICE: Opamp_Nichtinvertierend_02.asc

OpNonInv.asc

Version 4
SHEET 1 880 680
WIRE 96 -192 32 -192
WIRE 192 -176 160 -176
WIRE 272 -176 192 -176
WIRE 96 -160 80 -160
WIRE 192 -160 192 -176
WIRE 80 -80 80 -160
WIRE 192 -80 80 -80
WIRE 192 -64 192 -80
WIRE 112 80 48 80
WIRE 208 96 176 96
WIRE 288 96 208 96
WIRE 112 112 96 112
WIRE 96 144 96 112
WIRE 208 144 208 96
WIRE 208 144 96 144
FLAG 48 80 Ve
IOPIN 48 80 In
FLAG 288 96 Va1
IOPIN 288 96 Out
FLAG 192 16 0
FLAG 32 -192 Ve
IOPIN 32 -192 In
FLAG 272 -176 Va
IOPIN 272 -176 Out
SYMBOL Opamps\\opamp 144 160 M180
SYMATTR InstName U1
SYMBOL Opamps\\opamp 128 -112 M180
SYMATTR InstName U2
SYMBOL res 176 -176 R0
WINDOW 3 36 68 Left 2
SYMATTR InstName R1
SYMATTR Value 4k
SYMBOL res 176 -80 R0
WINDOW 3 36 68 Left 2
SYMATTR InstName R2
SYMATTR Value 1k
TEXT -24 -240 Left 2 !.include opamp.sub
TEXT -24 -272 Left 2 !VE VE 0 DC 0
TEXT -24 -312 Left 2 !.dc Ve -1 1 0.05

Version 4
SymbolType CELL
LINE Normal -32 32 32 64
LINE Normal -32 96 32 64
LINE Normal -32 32 -32 96
LINE Normal -9 50 -24 50
LINE Normal -9 76 -24 76
LINE Normal -16 84 -16 69
WINDOW 0 0 32 Left 0
SYMATTR Prefix X
SYMATTR Description Ideal single-pole operational amplifier. You must .lib opamp.sub
SYMATTR Value opamp
SYMATTR SpiceLine Aol=100K
SYMATTR SpiceLine2 GBW=10Meg
PIN -32 48 NONE 0
PINATTR PinName invin
PINATTR SpiceOrder 1
PIN -32 80 NONE 0
PINATTR PinName noninvin
PINATTR SpiceOrder 2
PIN 32 64 NONE 0
PINATTR PinName out
PINATTR SpiceOrder 3

Grundschaltung: Invertierender Verstärker

Knotenregel

$I = \frac{V_E}{R_1} = - \frac{V_A}{R_2}$
Verstärkung:

$v = - \frac{R_2}{R_1}$
Eingangswiderstand:

$R_{e} = R_{1}$

OpInv.asc

Version 4
SHEET 1 880 680
WIRE 112 16 96 16
WIRE 0 80 -32 80
WIRE 96 80 96 16
WIRE 96 80 80 80
WIRE 112 80 96 80
WIRE 192 96 192 16
WIRE 192 96 176 96
WIRE 208 96 192 96
WIRE 112 112 96 112
WIRE 96 160 96 112
FLAG -32 80 Ve
IOPIN -32 80 In
FLAG 208 96 Va
IOPIN 208 96 Out
FLAG 96 160 0
SYMBOL Opamps\\opamp 144 32 R0
SYMATTR InstName U1
SYMBOL res 96 64 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 28 56 VBottom 2
SYMATTR InstName R1
SYMATTR Value 1k
SYMBOL res 208 0 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 28 56 VBottom 2
SYMATTR InstName R2
SYMATTR Value 100k
TEXT -56 -40 Left 2 !VE VE 0 DC 0
TEXT -64 -72 Left 2 !.dc Ve -1 1 0.05
TEXT -56 -104 Left 2 !.include opamp.sub

Vergleich invertierender und nichtinvertierender OpAmp

Die Verstärkung wird durch R1 und R2 eingestellt.
Der Eingangswiderstand des nichtinvertierenden Verstärkers ist sehr groß.
Der invertierender Verstärker kann ohne R1 einen Eingangsstrom in eine Spannung wandeln
Der Ausgangswiderstand ist sehr niedrig.

Addierer

Berechnung der Ausgangsspannung

$U_a$

Knotengleichung:

$I_{R1} + I_{R2} + I_{R3} = I_{RN}$
Der ideale Operationsverstärker hat keinen Eingangsstrom.
Der Eingang Minus des Operationsverstärkers liegt wegen sehr grosser Verstärkung und negativer Rückkopplung auf Masse.
Knotengleichung und ohmsches Gesetz

$\frac{U_{e1}}{R_1} + \frac{U_{e2}}{R_2} + \frac{U_{e3}}{R_3} = - \frac{U_{a}}{R_N}$

$U_{a} = - \left( \frac{R_N}{R_1} \cdot U_{e1}+ \frac{R_N}{R_2} \cdot U_{e2} + \frac{R_N}{R_3} \cdot U_{e3} \right)$

OpAdder.asc

Version 4
SHEET 1 880 680
WIRE 0 -112 -32 -112
WIRE 96 -112 80 -112
WIRE 0 -16 -32 -16
WIRE 96 -16 96 -112
WIRE 96 -16 80 -16
WIRE 96 16 96 -16
WIRE 112 16 96 16
WIRE 0 80 -32 80
WIRE 96 80 96 16
WIRE 96 80 80 80
WIRE 112 80 96 80
WIRE 192 96 192 16
WIRE 192 96 176 96
WIRE 208 96 192 96
WIRE 112 112 96 112
WIRE 96 160 96 112
FLAG -32 80 Ve1
IOPIN -32 80 In
FLAG 208 96 Va
IOPIN 208 96 Out
FLAG 96 160 0
FLAG -32 -16 Ve2
IOPIN -32 -16 In
FLAG -32 -112 Ve3
IOPIN -32 -112 In
SYMBOL Opamps\\opamp 144 32 R0
SYMATTR InstName U1
SYMBOL res 96 64 R90
WINDOW 0 0 56 VBottom 0
WINDOW 3 32 56 VTop 0
SYMATTR InstName R1
SYMATTR Value ""
SYMBOL res 96 -32 R90
WINDOW 0 0 56 VBottom 0
WINDOW 3 32 56 VTop 0
SYMATTR InstName R2
SYMATTR Value ""
SYMBOL res 96 -128 R90
WINDOW 0 0 56 VBottom 0
WINDOW 3 32 56 VTop 0
SYMATTR InstName R3
SYMATTR Value ""
SYMBOL res 208 0 R90
WINDOW 0 0 56 VBottom 0
WINDOW 3 32 56 VTop 0
SYMATTR InstName RN
SYMATTR Value ""

Subtrahierer

Berechnung der Ausgangsspannung

$U_a$ .
Zur Lösung führt man die Spannung

$U_X$ am positiven Eingang des Operationsverstärkers ein.

Knotengleichungen

$I_{R1} = I_{RN} ; I_{R2} = I_{RP}$

$\frac{U_{e1} - U_x}{R_1} = \frac{U_{x} - U_a}{R_N}$ ;

$\frac{U_{e2}}{R_2 + R_P} = \frac{U_{x}}{R_P}$
2. Gleichungen nach

$U_x$ umformen und in Gleichung 1 einsetzen.

$\frac{U_{e1}}{R_1} - \frac{R_P \cdot U_{e2}}{R_1 \left( R_2 + R_P \right)} = \frac{R_P \cdot U_{e2}}{R_N \left( R_2 + R_P \right)} - \frac{U_a}{R_N}$

Umformen nach

$U_a$

$\frac{U_a}{R_N} = \frac{R_P \cdot U_{e2}}{R_N \left( R_2 + R_P \right)} - \frac{U_{e1}}{R_1} + \frac{R_P \cdot U_{e2}}{R_1 \left( R_2 + R_P \right)}$

$U_a = \frac{R_P \cdot U_{e2}}{ R_2 + R_P } - \frac{U_{e1} R_N}{R_1} + \frac{R_N \cdot R_P \cdot U_{e2}}{R_1 \left( R_2 + R_P \right)}$

$U_a = \frac{R_P}{ R_2 + R_P } \left( 1 + \frac{R_N}{R_1} \right) U_{e2} - \frac{ R_N}{R_1} U_{e1}$

$U_a = \frac{ R_N}{R_1} \left( \frac{ 1 + \frac{R_1}{R_N}}{1 + \frac{R_2}{ R_P}} U_{e2} - U_{e1} \right)$

mit

$\alpha = \frac{ R_N}{R_1} = \frac{ R_P}{R_2}$

$U_a = \alpha \left( U_{e2} - U_{e1} \right)$

subtrahierer.asc

Version 4
SHEET 1 880 680
WIRE 112 16 96 16
WIRE -16 48 -32 48
WIRE 96 48 96 16
WIRE 96 48 64 48
WIRE 96 80 96 48
WIRE 112 80 96 80
WIRE 192 96 192 16
WIRE 192 96 176 96
WIRE 208 96 192 96
WIRE 112 112 96 112
WIRE 64 128 48 128
WIRE 96 128 96 112
WIRE 96 128 64 128
WIRE 96 144 96 128
FLAG -32 48 Ve1
IOPIN -32 48 In
FLAG 208 96 Va
IOPIN 208 96 Out
FLAG 96 224 0
FLAG -32 128 Ve2
IOPIN -32 128 In
FLAG 64 128 Vx
SYMBOL Opamps\\opamp 144 32 R0
WINDOW 0 4 42 Left 2
SYMATTR InstName U1
SYMBOL res 80 32 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 63 56 VBottom 2
SYMATTR InstName R1
SYMATTR Value 100k
SYMBOL res 64 112 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 65 55 VBottom 2
SYMATTR InstName R2
SYMATTR Value 100k
SYMBOL res 208 0 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 63 57 VBottom 2
SYMATTR InstName RN
SYMATTR Value 100k
SYMBOL res 80 128 R0
WINDOW 3 36 68 Left 2
SYMATTR InstName RP
SYMATTR Value 100k
TEXT 176 136 Left 2 !V1 Ve1 0 SINE(0 1 1k)\nV2 Ve2 0 SINE(0 0 1k)
TEXT -50 200 Left 2 !.tran 4m
TEXT 128 232 Left 2 !.include opamp.sub

Subtrahierer mit hochohmigem Eingang

Subtrahierer mit hochohmigem Eingang
Instrumentationsverstärker

Symmetrische Betrachtung

$R_1 = R_N = R_2 = R_P$

$R_4 = R_5$

Subtrahierer: U1

$U_a = U_{a2} - U_{a1}$

Eingang:
Nichtinvertierender Verstärker

$U_{ai} = \left( 1 + 2 \cdot \frac{R_4}{R_3} \right) \cdot V_{ei}$

SubHoch.asc

Version 4
SHEET 1 880 680
WIRE -208 -80 -240 -80
WIRE -112 -64 -144 -64
WIRE -96 -64 -112 -64
WIRE -16 -64 -96 -64
WIRE 96 -64 64 -64
WIRE -208 -48 -224 -48
WIRE 96 -16 96 -64
WIRE 112 -16 96 -16
WIRE -224 32 -224 -48
WIRE -112 32 -112 16
WIRE -112 32 -224 32
WIRE -112 48 -112 32
WIRE 96 80 96 -16
WIRE 112 80 96 80
WIRE 192 96 192 -16
WIRE 192 96 176 96
WIRE 208 96 192 96
WIRE 112 112 96 112
WIRE 96 128 96 112
WIRE 96 128 80 128
WIRE -112 144 -112 128
WIRE -112 144 -224 144
WIRE 96 144 96 128
WIRE -112 160 -112 144
WIRE -224 240 -224 144
WIRE -208 240 -224 240
WIRE -112 256 -112 240
WIRE -112 256 -144 256
WIRE -80 256 -112 256
WIRE 0 256 0 128
WIRE 0 256 -80 256
WIRE -208 272 -240 272
FLAG -240 -80 Ve1
IOPIN -240 -80 In
FLAG 208 96 Va
IOPIN 208 96 Out
FLAG 96 224 0
FLAG -240 272 Ve2
IOPIN -240 272 In
FLAG -96 -64 Va1
FLAG -80 256 Va2
SYMBOL Opamps\\opamp 144 32 R0
SYMATTR InstName U1
SYMBOL res 80 -80 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 63 53 VBottom 2
SYMATTR InstName R1
SYMATTR Value 10k
SYMBOL res 96 112 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 61 55 VBottom 2
SYMATTR InstName R2
SYMATTR Value 10k
SYMBOL res 208 -32 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 64 57 VBottom 2
SYMATTR InstName RN
SYMATTR Value 10k
SYMBOL res 80 128 R0
WINDOW 3 36 68 Left 2
SYMATTR Value 10k
SYMATTR InstName RP
SYMBOL Opamps\\opamp -176 192 R0
SYMATTR InstName U2
SYMBOL res -128 32 R0
SYMATTR InstName R3
SYMATTR Value 10k
SYMBOL res -128 -80 R0
SYMATTR InstName R4
SYMATTR Value 10k
SYMBOL res -128 144 R0
SYMATTR InstName R5
SYMATTR Value 10k
SYMBOL Opamps\\opamp -176 0 M180
SYMATTR InstName U3
TEXT -120 288 Left 2 !Ve1 Ve1 0 DC 2\nVe2 Ve2 0 DC 1
TEXT 72 272 Left 2 !.dc Ve1 0 5 0.5
TEXT -192 -120 Left 2 !.include opamp.sub

Simulation, Praktischer Aufbau und Messung

TLC272 Baustein und Datenblatt
Spannungsversorgung
Eingangsspannungsbereich
Ausgangsspannungsbereich
Differenzspannung am Operationsverstärker

Die Differenzspannung am Eingang des Operationsverstärkers ist sehr klein und kaum messbar.
Differenzspannungsverstärkung vu = 4000.
Ausgangsspannungsamplitude

$\hat{u}_a = 2 V$
Differenzspannungsamplitude

$\hat{u}_d = \frac{\hat{u}_a}{v_u} = \frac{2 V}{4000} = 0.5 mV$

Die Eingangsspannungen müssen im Versorgungsspannungsbereich liegen.

Die Ausgangsspannung liegt im Versorgungsspannungsbereich und kann abgeschnitten werden.

Nächstes Mal:

20 Mitkopplung

2023 Elektronik 19 Operationsverstärkerschaltungen Prof. Dr. Joerg Vollrath