Elektronik

23 Induktivitäten und Kapazitäten

Prof. Dr. Jörg Vollrath

22 MOSFET Schaltungen

Video der 17. Vorlesung 1.12.2020

Länge: 01:28:01

0:0:10 Komplexer Widerstand

0:5:16 Internet Übung komplexer Widerstand

0:10:32 Eckfrequenz, Übertragungsfunktion

0:21:46 Komplexer Widerstand

0:25:28 Gleichung, Simulation, Messung von Bauteilen

0:28:54 Lineare Modelle

0:31:41 Widerstandsmessung

0:34:54 Kapazitätsmessung Anwendung Differentialgleichung

0:40:48 Induktivitätsmessung

0:43:4 Electronic Explorer

0:47:40 Spannungsquellen, Stromquellen

0:48:39 Ideale Spannungsquelle

0:51:54 Ideale Stromquelle

0:53:9 Reale Spannungsquelle

1:1:9 Electronic Explorer Spannungsquelle

1:4:39 Quellenumwandlung

1:7:43 Wechselspannungsquelle

1:10:8 Frequenzgang

1:11:14 Gesteuerte Quellen

1:13:58 Zusammenfassung

Video Quellenmessung 2.6.2022

Länge: 20:00

Video Bodediagram RC Messung 2.6.2022

Länge: 10:00

Übersicht

Elemente mit 2 Anschlüssen

Aktiv: Stromquelle, Spannungsquelle
Reale Quellen: Innenwiderstand
Passiv: R, L, C

Verhalten

Statische Gleichung, Kennlinie: I(U)
Übertragungsfunktion: U1/U2(jw)
Simulation: LTSPICE
Messung: Oszilloskop

Lernziele

Sie kennen Modelle von Bauelementen

Sie können von einem Bauteil ein Modell erstellen

Statische und dynamische UI-Messung:
R, L, C.

Lineare Modelle

Einfache 2-polige lineare Bauelemente

R statische Kennlinie U = R · I
L, C: $U = - L \frac{dI}{dt}$ $I = C \frac{dU}{dt}$
U = j ω L · I ; $U = \frac{I}{j \omega C}$
U, I :Spannungsquellen, Stromquellen

Kombinierte Bauelemente

Reale Quellen: U, I, Z
Tiefpass, Hochpass: R, C, L

4-polige lineare Bauelemente

Gesteuerte Quellen

Modelle.asc

Version 4
SHEET 1 880 680
WIRE 96 144 48 144
WIRE 192 144 176 144
WIRE 288 144 224 144
WIRE 352 144 288 144
WIRE 400 144 384 144
WIRE 496 144 480 144
WIRE 512 144 496 144
WIRE 48 160 48 144
WIRE 224 160 224 144
WIRE 288 160 288 144
WIRE 496 160 496 144
WIRE 48 256 48 240
WIRE 192 256 48 256
WIRE 224 256 224 240
WIRE 288 256 288 240
WIRE 288 256 224 256
WIRE 352 256 288 256
WIRE 496 256 496 224
WIRE 496 256 384 256
WIRE 512 256 496 256
WIRE 128 320 80 320
WIRE 272 320 224 320
WIRE 448 320 352 320
WIRE 128 352 128 320
WIRE 224 352 224 320
WIRE 128 464 128 432
WIRE 128 464 80 464
WIRE 224 464 224 432
WIRE 448 464 224 464
FLAG 128 320 Vinp
FLAG 128 464 Vinm
SYMBOL res 80 -16 R0
SYMATTR InstName R1
SYMBOL ind 160 -16 R0
SYMATTR InstName L1
SYMBOL cap 240 0 R0
SYMATTR InstName C1
SYMBOL voltage 336 -16 R0
SYMATTR InstName V1
SYMBOL current 432 0 R0
SYMATTR InstName I1
SYMBOL current 224 160 R0
SYMATTR InstName I2
SYMBOL res 192 128 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R2
SYMBOL res 272 144 R0
SYMATTR InstName R3
SYMBOL voltage 48 144 R0
SYMATTR InstName V2
SYMBOL bv 224 336 R0
SYMATTR InstName B1
SYMATTR Value V={VU}*(V(Vinp)-V(Vinm))
SYMBOL res 112 336 R0
SYMATTR InstName R4
SYMBOL res 368 304 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R5
SYMBOL res 496 128 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R6
SYMBOL cap 480 160 R0
SYMATTR InstName C2

Widerstandsmessung

UI Kennlinie

Strommessung
Magnetfeld, Messwiderstand
Lineare UI-Kennlinie
Steigung ist der Leitwert

$R = \frac{U}{I} = \frac{U2}{\frac{U_1 - U_2 }{R_{Mess}}}$

$R = \frac{U2 \cdot R_{Mess} }{U_1 - U_2}$

WiderstandsmessungA.asc

Version 4
SHEET 1 880 680
WIRE 144 48 80 48
WIRE 320 48 224 48
WIRE 320 80 320 48
WIRE 80 96 80 48
WIRE 80 192 80 176
WIRE 192 192 80 192
WIRE 320 192 320 160
WIRE 320 192 192 192
WIRE 192 208 192 192
FLAG 192 208 0
FLAG 80 48 U1
FLAG 320 48 U2
SYMBOL voltage 80 80 R0
SYMATTR InstName V1
SYMATTR Value 1
SYMBOL res 240 32 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName Rmess
SYMATTR Value 100
SYMBOL res 304 64 R0
SYMATTR InstName RX
SYMATTR Value 80
TEXT 80 248 Left 2 !.dc V1 -1 1 0.01

Der Messwiderstand muss in der Größenordnung des zu messenden Widerstands sein.
Bild: Messaufbau und xy-Darstellung Electronic Explorer

Grundzweipole

Idealer Ohmscher Zweipol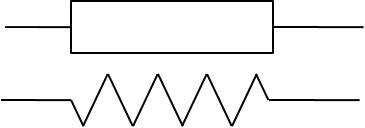

Idealer induktiver Zweipol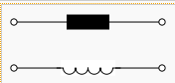

Idealer kapazitiver Zweipol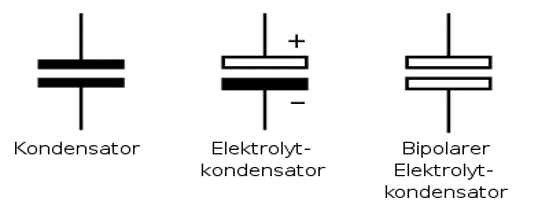

Induktivität und Kapazität

Eine Kapazität wirkt bei angelegter Gleichspannung wie eine Unterbrechung
Alufolie mit Papierisolator
Eine Induktivität wirkt bei angelegter Gleichspannung wie ein Kurzschluss
Gewickelte Spule

Wechselspannungsmessung

Signalform: Sinus, Rechteck
Frequenz, Amplitude
Frequenzabhängiger Widerstand
Phasenverschiebung zwischen Strom und Spannung

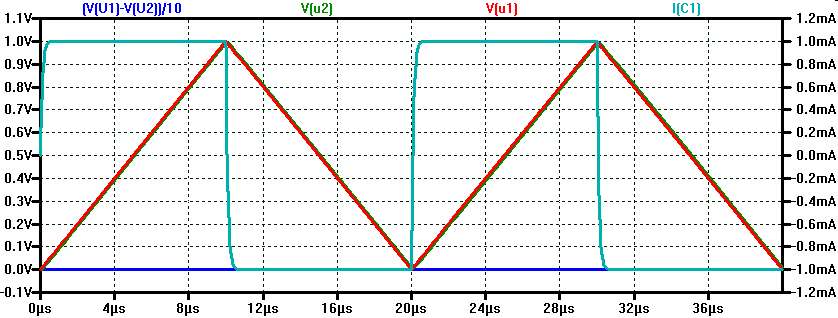
Kapazitätsmessung dU/dt

Strommessung

mit Spannungsrampe

Messwiderstand
Lineare UI-Kennlinie
Steigung ist der Leitwert

$I = C \frac{dU}{dt}$

$C = \frac{I \cdot dt}{dU} = \frac{ 1 mA \cdot 10 \mu s }{1 V} = 10 nF$

KapazitaetMessung.asc

Version 4
SHEET 1 880 680
WIRE 144 48 80 48
WIRE 320 48 224 48
WIRE 320 80 320 48
WIRE 80 96 80 48
WIRE 80 192 80 176
WIRE 192 192 80 192
WIRE 320 192 320 144
WIRE 320 192 192 192
WIRE 192 208 192 192
FLAG 192 208 0
FLAG 80 48 U1
FLAG 320 48 U2
SYMBOL voltage 80 80 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V1
SYMATTR Value PULSE(0 1 0 10u 10u 0 20u 10)
SYMBOL res 240 32 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName Rmess
SYMATTR Value 100
SYMBOL cap 304 80 R0
SYMATTR InstName C1
SYMATTR Value 10n
TEXT 104 248 Left 2 !.tran 40u

Es gilt folgende Formel für die Kapazität:

$C = \frac{Q}{U} = \frac{I dt}{dU}$
Man erzeugt eine Dreiecksspanung dU/dt = konstant und misst den Strom.
LTSPICE: PULSE(0 1 0 10u 10u 0 20u 10)
Der Spannungspuls geht von 0 V (low Pegel) bis zu 1 V (high Pegel). Die Periodendauer der Dreieckspannung ist 20 us. 10 us steigt die Spannung, 10us fällt die Spannung und ist 0 s high.
Es fliesst ein Strom von +-1 mA.
Die Spanungsänderung dU/dt und der Messwiderstand muss an die Kapazität angepasst werden.
Beim Beispiel bekommt man am Widerstand R = 10 Ohm 1% Genauigkeit und einer Spannungsänderung von 1V/10us, einen Strom von 1 mA, einen Spannungsabfall an Rmess von 10 mV, der mit dem Oszilloskop gemessen werden muss.
Besser wäre ein Vorwiderstand von 100 Ohm, der unter gleichen Messbedingungen einen Spannungsabfall von 100 mV erzeugt.
Eine 10 Bit Auflösung des Oszilloskops würde bei einem Eingangsbereich von 0..1V eine Auflösung von 1mV ergeben. Das könnten bei differentiellen Probes oder nach Offset-Abgleich, dann 10%/1% Genauigkeit sein.

Induktivitätsmessung mit Übertragungsfunktion

$\frac{\underline{U}_{out}}{\underline{U}_E} = \frac{R_{L1} + j \omega L_1}{R_{L1} + R_{Mess} + j \omega L_1}$
R_Mess = 100 Ω
U_{E AC} = 1 V

ω = 0 s^-1

$\frac{U_{out}}{U_E} = \frac{R_{L1}}{R_{L1} + R_{Mess}}$

$R_{L1} = \frac{R_{Mess}}{ \frac{U_E}{U_{out}} - 1 } = \frac{100 \Omega}{ \frac{1 V}{0.074} - 1 } = 8 \Omega$

Eckfrequenz: 3dB = 20 log

$\sqrt{2}$ und φ = 45°

$L_{1} = \frac{R_{L1} + R_{Mess}}{\omega} = \frac{R_{L1} + R_{Mess}}{2 \pi f_{3dB}}$

Induktivitaetsmess.asc

Version 4
SHEET 1 880 680
WIRE 176 112 112 112
WIRE 320 112 256 112
WIRE 400 112 320 112
WIRE 496 112 480 112
WIRE 496 144 496 112
WIRE 112 176 112 112
WIRE 112 288 112 256
WIRE 496 288 496 224
FLAG 112 288 0
FLAG 320 112 Uout
FLAG 496 288 0
SYMBOL voltage 112 160 R0
WINDOW 123 24 124 Left 2
WINDOW 39 0 0 Left 2
SYMATTR Value2 AC 1
SYMATTR InstName V1
SYMATTR Value SINE(0 1 1k)
SYMBOL res 272 96 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName RMess
SYMATTR Value 100
SYMBOL res 496 96 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName RL1
SYMATTR Value 8
SYMBOL ind 480 128 R0
SYMATTR InstName L1
SYMATTR Value 15�
TEXT 288 192 Left 2 !;tran 4m
TEXT 288 224 Left 2 !.ac dec 10 1 1G

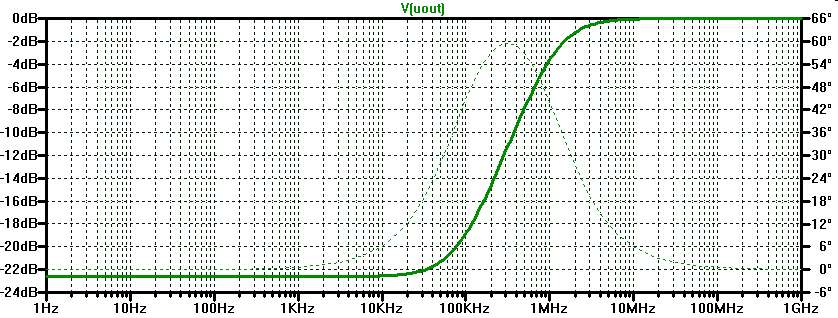
Eine Übertragungsfunktion einer Wechselspannungsschaltung stellt das frequenzabhängige Amplitudenverhältnis und Phasenverhältnis zwischen Ausgangsspannung und Eingangsspannung dar.
Dabei wird auf der x-Achse die Frequenz logarithmisch und auf der y-Achse das Maß in dB aufgetragen (Bild rechts unten).
Die Umrechnung von einem Spannungsverhältnis U2/U1 in ein Maß a erfolgt durch folgende Glechung:

$a = 20 log_{10} | \frac{U_2}{U_1}|$
Frequenzenzen bei denen sich die Steigung des Amplitudenverhältnisses (Maß) ändert werden als Eckfrequenzen bezeichnet und bei einer Änderung von 3 dB oder einer Phasenänderung von 45° abgelesen.
Zur Bestimmung der Eckfrequenzen wird die komplexe Übertragungsfunktion der Schaltung aufgestellt. Im Beispiel das Verhältnis von dem Reihenwiderstand RL1 und L1 zum Gesamtreihenwiderstand von RMess, RL1 und L1 (Spannungsteiler).
Der komplexe Widerstand der Induktivität L1 ist:

$\underline{Z}_{L1} = j \omega L1$
wobei ω die Kreisfrequenz ist.
Die Schaltung hat 2 Eckfrequenzen:
Zähler der Übertragungsfunktion bei dem

$Im\{\underline{Z}\} = Re\{\underline{Z}\}$

$R_{L1} = \omega L_1$
Nenner der Übertragungsfunktion bei dem

$Im\{\underline{Z}\} = Re\{\underline{Z}\}$

$R_{L1} + R_{Mess} = \omega L_1$
Bei Waveforms aktiviert man den Network Analyzer.

LTSPICE Übertragungsfunktion:

$\frac{U_{out}}{U_E} = (1 Hz) = -23 dB = 0.074$

$L_{1} = \frac{8 \Omega + 100 \Omega }{2 \pi 1 MHz} = 15 \mu H$

Wechselspannungsquelle: Frequenzgang

Spannungsbereich
Maximalfrequenz
Kopfhörer, Lautsprecher
Übertragungsfunktion

Frequenzgang

Messgerät: Netzwerkanalysator, Spektrumanalysator Lautsprecherweiche Hochtöner, Tieftöner	Sinuslive 3-Wege-Frequenzweiche CR345

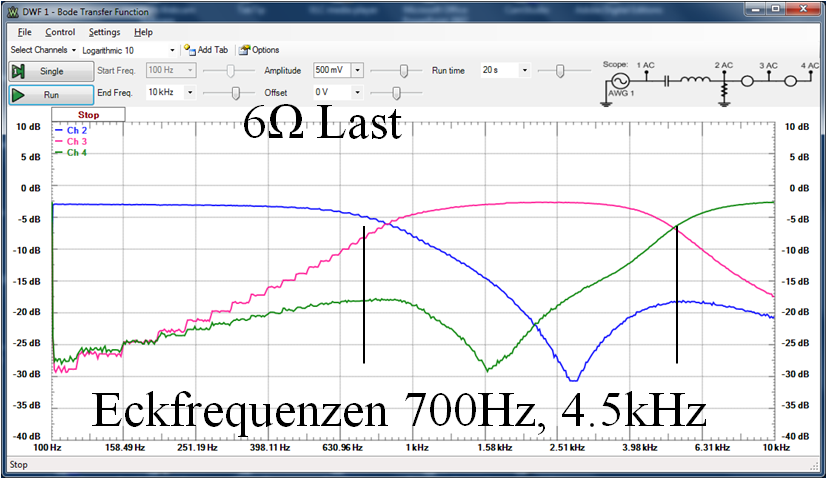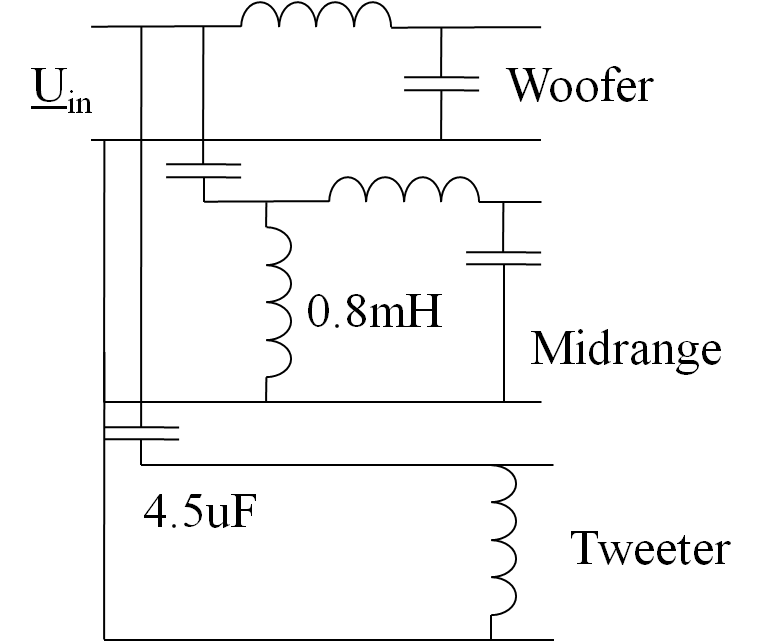Messung mit R, L und C bei 20 kHz

R = 100 Ω
C1 = 45 nF
L1 = 2.18 mH, 20 Ω

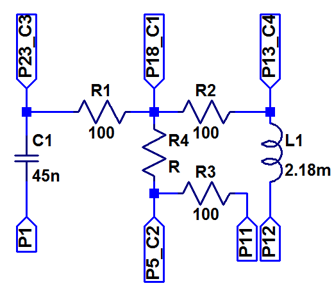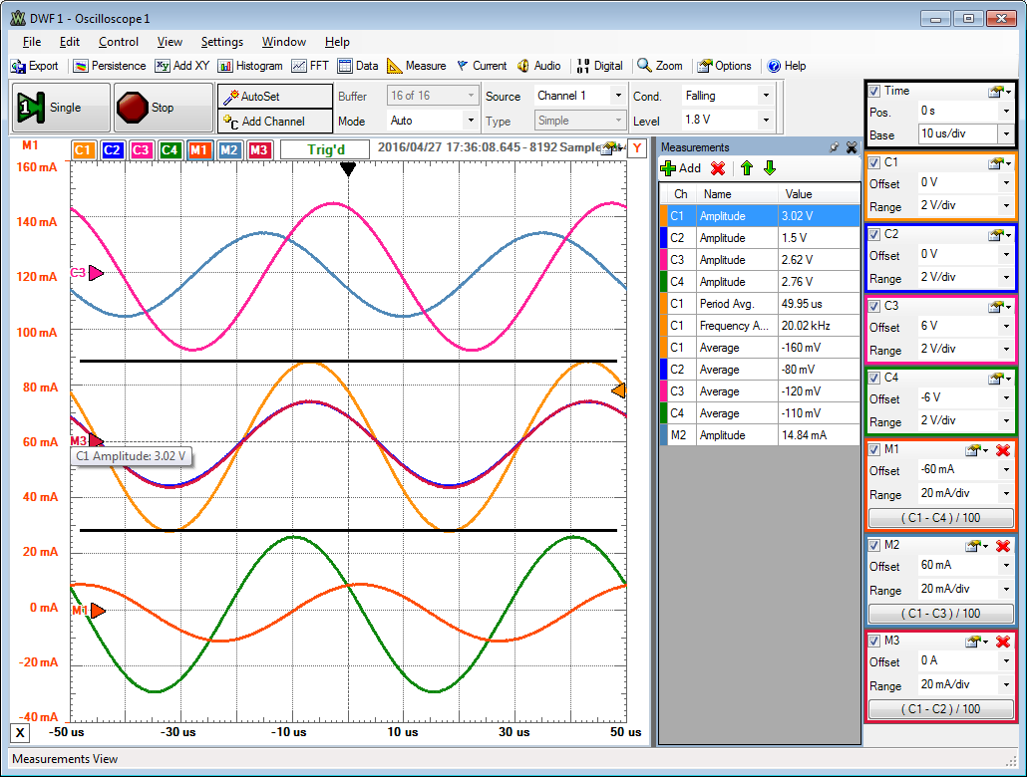Spannungen und Widerstände werden mit komplexen Symbolen dargestellt.

Jede reale Spule hat einen ohmschen Widerstand und eine Induktivität.

Fragen:

Was ist eine Oszilloskop?
Was beobachten Sie?
Welche Kenngrößen einer Sinusschwingung gibt es?
Was passiert, wenn man diese verändert?

Die Schaltung wird mit dem Electronic Explorer Board verbunden.
P18 AWG1, OSC1; P1,P11,P12, GND; P5 OSC2 (R), P23 OSC3 C, P13 OSC4 (L)
Berechnung der Ströme:
IR: M1 = (C1 -C4) / 100
IC: M2 = (C1-C3)/100
IL: M3 = (C1-C2)/100

Oszilloskop

In einem festen Zeitraster werden Spannungen mit einem Analog-Digital-Wandler erfasst.
Das Zeitraster (Time, Base), x-Achse und die Spannungsauflösung (Range), y-Achse kann man einstellen.
Mit der Position und dem Offset kann man die Darstellung nach rechts oder links bzw. oben oder unten verschieben.
Ein Trigger (Source, Condition, Level) sorgt für ein stehendes Bild.

Messung

Kapazität

	f	20 kHz	50 kHz	10 kHz
C3	U	2.6 V	1.74 V	2.9 V
M2	I	15 mA	24.6 mA	8.3 mA

Je höher die Frequenz, desto kleiner der Widerstand.

$\frac{U}{I} = \frac{1}{\omega C}$

$\frac{\underline{U}}{\underline{I}} = \frac{1}{j \omega C} = \underline{Z}_C$

Induktivität

	f	20 kHz	50 kHz	10 kHz
C4	U	2.72 V	2.95 V	2.2 V
M1	I	10.54 mA	4.79 mA	17.48 mA

Je höher die Frequenz, desto größer der Widerstand.

$\frac{\underline{U}}{\underline{I}} = j \omega L = \underline{Z}_L$

Induktivität

Differentialgleichung

$u_{L} = L \frac{d I}{d t}$

Komplexer Widerstand

$\underline{u}(t) = \hat{u} e^{j(\omega t + \phi_{u})}$

$\underline{Z} = j \omega L$

Komplexes Ohmsches Gesetz

$\underline{U} = j \omega L \underline{I}$

Kapazität

$C = \frac{Q}{U}$

Differentialgleichung

$i_{C} = C \frac{d U}{d t}$

Komplexer Widerstand

$\underline{u}(t) = \hat{u} e^{j(\omega t + \phi_{u})}$

$\underline{Z} = \frac{1}{j \omega C}$

Komplexes Ohmsches Gesetz

$\underline{U} = \frac{\underline{I}}{j \omega C}$

Zusammenfassung

Bauelementmodelle können anhand von UI Kennlinien (statisch), Signalmessungen und Frequenzgangsmessungen (dynamisch) bestimmt werden.
Geeignete Messbereiche und Messwiderstände müssen gewählt werden.
Ein Bauelementmodell ist nur so genau, wie die verwendeten Elemente

Nächstes Mal: 24 Testklausur

2023 Elektronik 23 L und C Prof. Dr. Joerg Vollrath

Elektronik

23 Induktivitäten und Kapazitäten

Prof. Dr. Jörg Vollrath

Video der 17. Vorlesung 1.12.2020

Video Quellenmessung 2.6.2022

Video Bodediagram RC Messung 2.6.2022

Übersicht

Lernziele

Sie kennen Modelle von Bauelementen

Sie können von einem Bauteil ein Modell erstellen

Lineare Modelle

Widerstandsmessung

UI Kennlinie

Grundzweipole

Induktivität und Kapazität

Wechselspannungsmessung

Kapazitätsmessung dU/dt

Strommessung

mit Spannungsrampe

Induktivitätsmessung mit Übertragungsfunktion

Wechselspannungsquelle: Frequenzgang

Frequenzgang

Messung mit R, L und C bei 20 kHz

Spannungen und Widerstände werden mit komplexen Symbolen dargestellt.

Fragen:

Oszilloskop

Messung

Induktivität

Differentialgleichung

Komplexer Widerstand

Komplexes Ohmsches Gesetz

Kapazität

Differentialgleichung

Komplexer Widerstand

Komplexes Ohmsches Gesetz

Zusammenfassung