Grundlagen Elektrotechnik 2 (GET2)

7 Ersatzquellen

Prof. Dr. Jörg Vollrath

06 Komplexe lineare Zweipole

Rückblick und Heute

Komplexer Widerstand und Leitwert

Z = R + j X Y = G + j B
Blindwiderstand X, Blindleitwert B

Umrechnung
Konjugiert komplex erweitern
Lineare passive Zweipole

Ideale und lineare aktive Zweipole

Ersatzquellen

Beispiele, Zeigerdiagramm
SPICE Simulation
Leistung

Ideale Sinusquelle

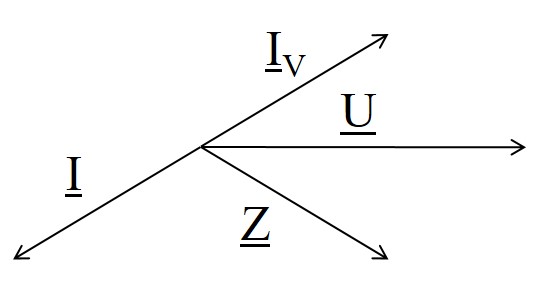
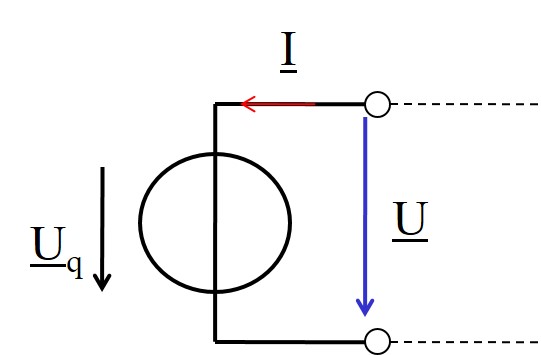
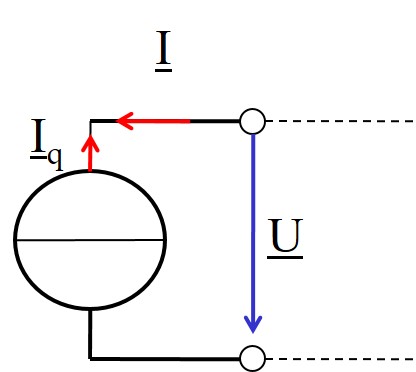
Ideale Sinusspannungsquelle Effektivwert Nullphasenwinkel Frequenz Leerlaufspannung Kein Kurzschlussbetrieb
Ideale Sinusstromquelle Effektivwert Nullphasenwinkel Frequenz Kurzschlussstrom Kein Leerlaufbetrieb

Eine Quelle φ_u = 0, φ_i = 0
Erzwungene Schwingung (forced oscillation)

Beispiel

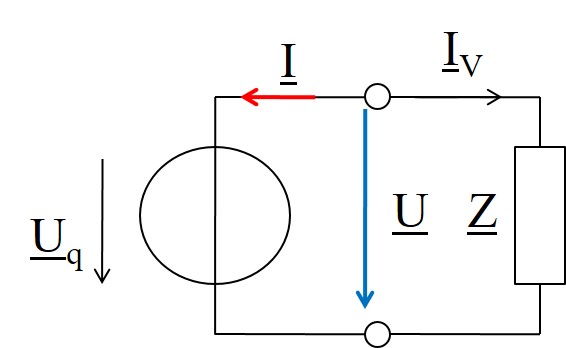
Eine ideale Sinusspannungsquelle mit der Quellenspannung U_q = 10 V /0° wird mit dem komplexen Widerstand Z = 4 Ω /-60° belastet. Wir wollen die Ströme im passiven sowie im aktiven Zweipol berechnen und sämtliche Sinusgrößen im Zeigerdiagramm darstellen.

$\underline{I}_V = \frac{\underline{U}}{\underline{Z}} = \frac{10 V}{4 \Omega} \underline{/0°-(-60°)} = 2.5 A \underline{/60°}$

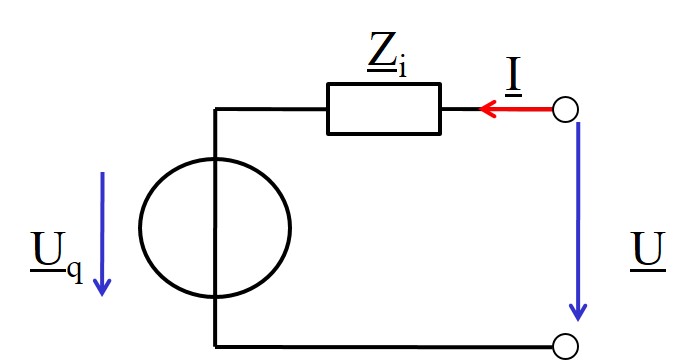
Lineare Sinusquelle

Die Reihenschaltung aus idealer Spannungsquelle und einem linearen Zweipol hat einen endlichen Kurzschlussstrom.
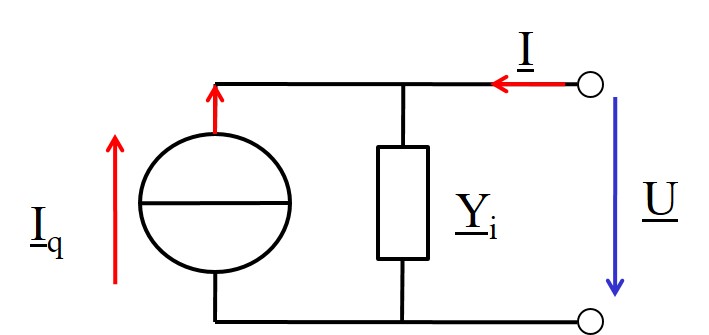
Die Parallelschaltung aus einer idealen Stromquelle und einem linearen Zweipol hat eine endliche Leerlaufspannung
Der Zusammenhang zwischen Quellengrößen lässt sich durch eine lineare Gleichung oder Differenzialgleichung beschreiben.

Lineare Ersatzquelle

Lineare aktive Zweipole, lineare Sinusquellen

Lineare Spannungsquelle $\underline{U}_q = \underline{U}_O$ $\underline{Z}_i = \frac{\underline{U}_O}{\underline{I}_K}$	Lineare Stromquelle $\underline{I}_q = \underline{I}_K$ $\underline{Y}_i = \frac{\underline{I}_K}{\underline{U}_O}$
Umwandlung
$\underline{U}_q = \underline{I}_q \cdot \underline{Z}_i$	$\underline{I}_q = \frac{\underline{U}_q}{\underline{Z}_i}$

$\underline{Y}_i = \frac{1}{\underline{Z}_i}$

Beispiel

Die Reihenschaltung aus einer idealen Spannungsquelle U_q = 24 V /0° und einem Zweipol Z_i = 4 kΩ /60° bildet eine lineare Spannungsquelle nach folgendem Bild. Wir wollen Leerlaufspannung und Kurzschlussstrom berechnen und die Daten für die äquivalente Ersatzstromquelle bestimmen.

$\underline{I}_K = \frac{\underline{U}_q}{\underline{Z}_i} = \frac{24 V}{4 k \Omega } \underline{/-60°} = 6 mA \underline{/-60°}$

$\underline{Y}_i = \frac{1}{\underline{Z}_i} = \frac{1}{4 k \Omega } \underline{/-60°} = 0.25 mS \underline{/-60°}$

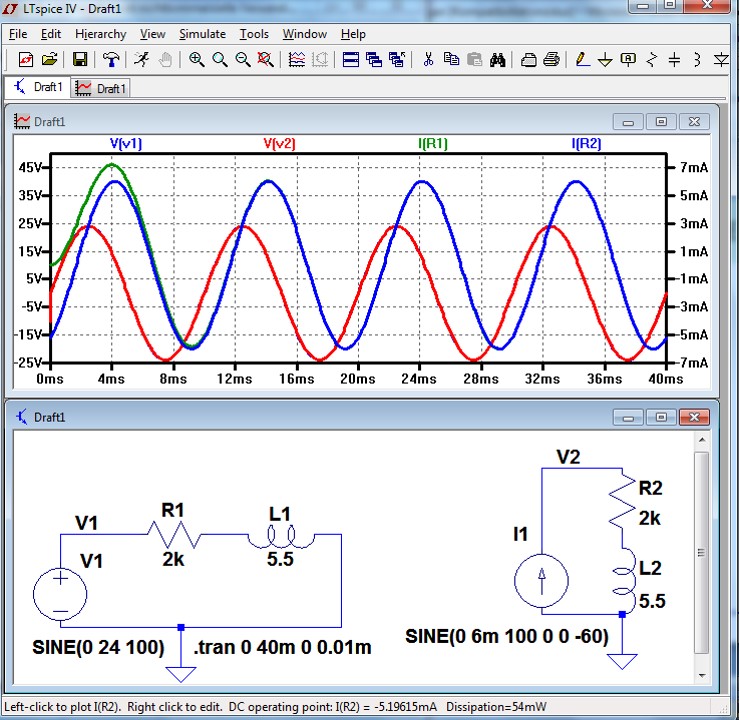
SPICE

f = 100 Hz
ω = 2 π f = 2 π 100 Hz = 628 rad/s
Z_i = R_i + j X_i
R_i = Z_i cos φ_i = 2 kΩ
X_i = Z_i sin φ_i = 3.46kΩ = ωL
L = 3.46kΩ / 628 rad/s = 5.5H
I_k eilt U_q nach

Demo SPICE

ErsatzQuelle02.asc

Achtung
Richtungen
Stromrichtung
Quellen
Verbraucher

Einschwingvorgang

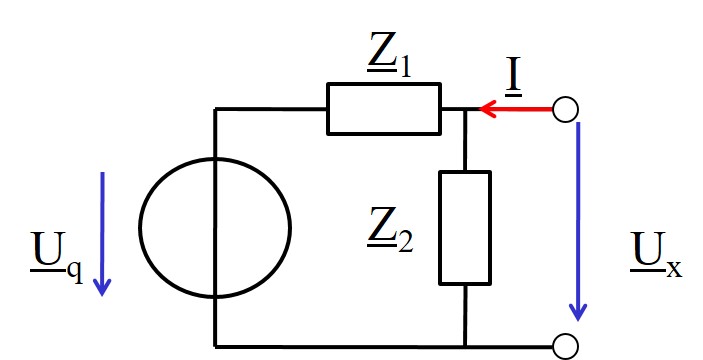
Beispiel Ersatzquelle

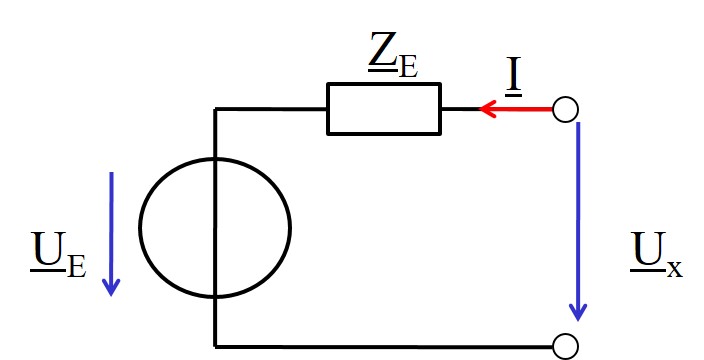
Geben Sie die Ersatzquellen (Strom, Spannung) zu folgender Schaltung an:

$\underline{U}_q = 10 V \underline{/ 0°};$

$\underline{Z}_1 = 100 \Omega + j 20 \Omega;$

$\underline{Z}_2 = 50 \Omega - j 40 \Omega;$

$\underline{Z}_E = \underline{Z}_1 || \underline{Z}_2 = \frac{1}{\frac{1}{\underline{Z}_1} + \frac{1}{\underline{Z}_2}}$

$\underline{Z}_E = \frac{\underline{Z}_1 \cdot \underline{Z}_2}{\underline{Z}_1 + \underline{Z}_2}$

$\underline{Z}_1 = \sqrt{100 \Omega \cdot 100 \Omega + 20 \Omega \cdot 20 \Omega } \underline{/ arctan\frac{20 \Omega}{100 \Omega}} = 102 \Omega \underline{/11.3°}$

$\underline{Z}_2 = \sqrt{50 \Omega \cdot 50 \Omega + 40 \Omega \cdot 40 \Omega } \underline{/ arctan\frac{-40 \Omega}{50 \Omega}} = 64 \Omega \underline{/-38.7°}$

$\underline{Z}_E = \frac{6530 \Omega \underline{/-27.3°}}{150 \Omega - j 20 \Omega} = \frac{6530 \Omega \underline{/-27.3°}}{151 \Omega \underline{/-7.6°}} = 43.2 \Omega \underline{/-19.7°} = 40.6 \Omega - j 14.6 \Omega$

$\underline{U}_E = \frac{\underline{Z}_2}{\underline{Z}_1 + \underline{Z}_2} \underline{U}_q = \frac{64 \Omega \underline{/-38.7°}}{151 \Omega \underline{/-7.6°}} \underline{U}_q = 10 V \underline{/ 0°} = 4.23 V \underline{/-31°}$

$\underline{I}_K = \frac{\underline{U}_q}{\underline{Z}_1} = 98 mA \underline{/-11.3°}$

Praxisbezug

Das 230V Versorgungsnetz kann für geringe Belastung als ideale Spannungsquelle angesehen werden. (Starres Netz)

Schließt man ans 230V Netz einen linearen Verbraucher hoher Leistung an, so können sich Effektivwert und Nullphasenwinkel der Netzspannung ändern. Sinusform und Frequenz ändern sich praktisch nicht. (Lineare Spannungsquelle)

Test Ersatzquelle

Eine ideale Sinusspannungsquelle mit der Quellenspannung

$\underline{U}_1 = 5 V \underline{/ 0°};$ wird mit einem Widerstand R₁ = 20 Ohm und einer Kapazität C₁ = 500 nF beschaltet.
Berechnen und zeichnen Sie die äquivalente Spannungsquelle und äquivalente Stromquelle bei 40 kHz.

$\underline{U}_L = \underline{I} \cdot \underline{Z}_{C1} = \underline{I} \frac{1}{j \omega C_1} = \underline{U}_1 \frac{1}{R_1 + \frac{}{j \omega C_1}} \frac{1}{j \omega C_1} = \underline{U}_1 \frac{1}{1 + j \omega C_1 R_1}$

$\underline{I} = \frac{\underline{U}}{\underline{Z}}$

$\underline{U}_L = \underline{U}_1 \frac{\frac{1}{j \omega C_1}}{R_1 + \frac{1}{j \omega C_1}}$

$j \omega C_1 R_1 = j 2.5 = 2.5 \underline{/90°}$

$1 + j \omega C_1 R_1 = 1 + j 2.5 = \sqrt{1^2 + 2.5^2} \underline{/arctan\frac{2.5}{1}} = 2.7 \underline{/68°}$

$\underline{U}_L = \frac{\underline{U}_1}{ 1 + j \omega C_1 R_1} = \frac{5 V}{2.7} \underline{/0°-68°} = 1.85 V \underline{/-68°}$

$\underline{I}_K = \frac{\underline{U}_1}{R_1} = \frac{5 V}{20 \Omega} \underline{/0°}$

$\underline{Z}_i = \frac{1}{\frac{1}{R_1} + j \omega C_1} \frac{R_1}{R_1} = \frac{R_1}{1 + j \omega C_1 R_1} = \frac{20 \Omega}{2.7 \underline{/68°}} = 7.4 \Omega \underline{/-68°}$

ErsatzQuelleURC.asc

Version 4
SHEET 1 880 680
WIRE 32 96 0 96
WIRE 80 96 32 96
WIRE 240 96 160 96
WIRE 304 96 240 96
WIRE 32 128 32 96
WIRE 240 144 240 96
WIRE 32 224 32 208
WIRE 240 224 240 208
WIRE 240 224 32 224
WIRE 304 224 240 224
WIRE 304 240 304 224
FLAG 304 240 0
FLAG 304 96 U
FLAG 0 96 V1
SYMBOL voltage 32 112 R0
WINDOW 123 24 124 Left 2
WINDOW 39 0 0 Left 2
SYMATTR Value2 AC 1
SYMATTR InstName V1
SYMATTR Value SINE(0 5 40k)
SYMBOL cap 224 144 R0
SYMATTR InstName C1
SYMATTR Value 500n
SYMBOL res 176 112 M270
WINDOW 0 32 56 VTop 2
WINDOW 3 0 56 VBottom 2
SYMATTR InstName R1
SYMATTR Value 20
TEXT 136 264 Left 2 !.tran 400u

Zusammenfassung und nächstes Mal

Ideale und reale Quellen
Quellenumwandlung, Ersatzquellen

08 Leistung

2022 GET 2 07 Ersatzquellen Prof. Dr. Joerg Vollrath

Grundlagen Elektrotechnik 2 (GET2)

7 Ersatzquellen

Prof. Dr. Jörg Vollrath

Video der 19. Vorlesung 8.6.2021

Rückblick und Heute

Ideale Sinusquelle

Beispiel

Lineare Sinusquelle

Lineare Ersatzquelle

Beispiel

SPICE

Demo SPICE

Beispiel Ersatzquelle

Praxisbezug

Test Ersatzquelle

Zusammenfassung und nächstes Mal