Grundlagen Elektrotechnik 2 (GET2)

09 Induktivität und Kapazität

Prof. Dr. Jörg Vollrath

Rückblick und Übersicht

Leistung

Scheinleistung	S = U I	VA	Voltampere
Wirkleistung	P = S cosφ	W	Watt
Blindleistung	Q = S sinφ	var	volt ampere reactive
Lesitungsfaktor	λ = P / S = cosφ

Komplexe Leistung:

\( \underline{S} = \underline{U} \underline{I}^{*} = \underline{Z} I^{2} = \underline{Y}^{*} U^{2} = P + j Q \)

Widerstand, Kapazität, Induktivität

Grundzweipole

Idealer Ohmscher Zweipol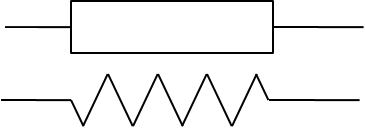

Idealer induktiver Zweipol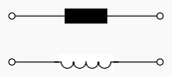

Idealer kapazitiver Zweipol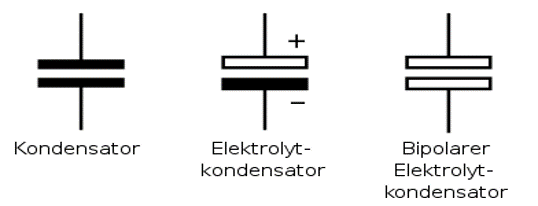

Ziele

Zusammenhang zwischen Sinuspannung und Sinusstrom an Grundzweipolen angeben
Phasenverschiebung erläutern
Komplexer Widerstand und Leitwert der Grundzweipole in P- und R-Form angeben
Leistungsgrößen bei Sinusspannung an den Grundzweipolen nennen

Messung mit R, L und C bei 20 kHz

R = 100 Ω
C1 = 45 nF
L1 = 2.18 mH, 20 Ω

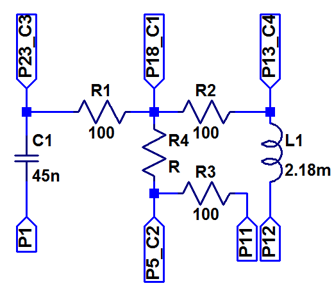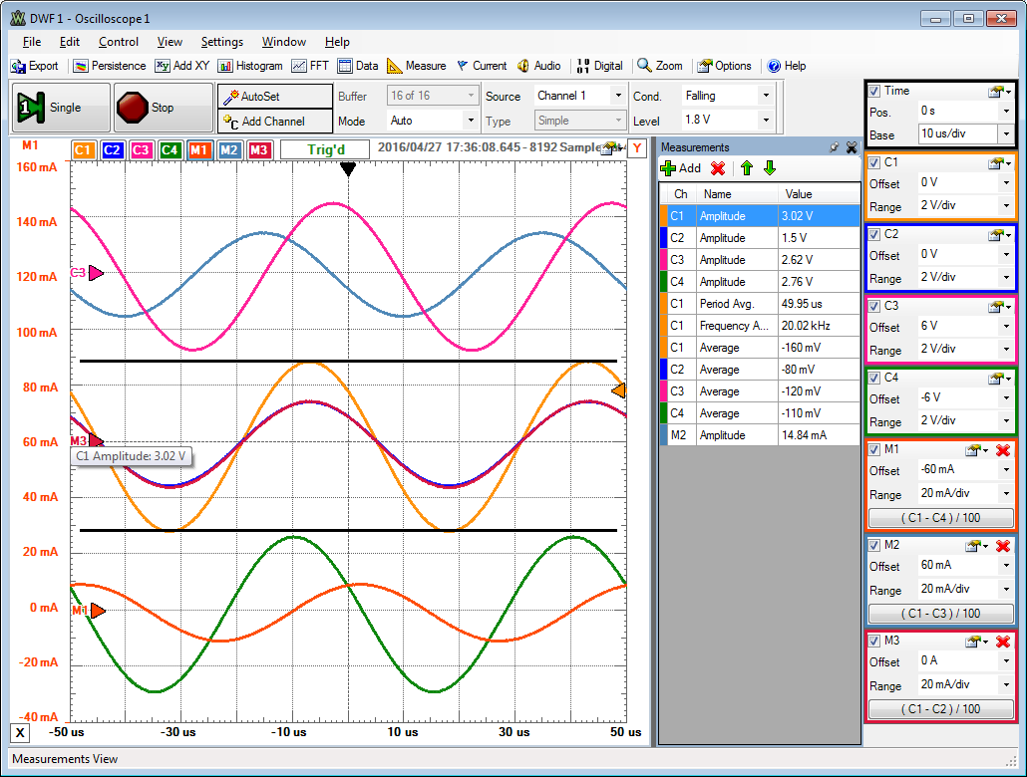Spannungen und Widerstände werden mit komplexen Symbolen dargestellt.

Jede reale Spule hat einen ohmschen Widerstand und eine Induktivität.

Fragen:

Was ist eine Oszilloskop?
Was beobachten Sie?
Welche Kenngrößen einer Sinusschwingung gibt es?
Was passiert, wenn man diese verändert?

Die Schaltung wird mit dem Electronic Explorer Board verbunden.
P18 AWG1, OSC1; P1,P11,P12, GND; P5 OSC2 (R), P23 OSC3 C, P13 OSC4 (L)
Berechnung der Ströme:
IR: M1 = (C1 -C4) / 100
IC: M2 = (C1-C3)/100
IL: M3 = (C1-C2)/100

Oszilloskop

In einem festen Zeitraster werden Spannungen mit einem Analog-Digital-Wandler erfasst.
Das Zeitraster (Time, Base), x-Achse und die Spannungsauflösung (Range), y-Achse kann man einstellen.
Mit der Position und dem Offset kann man die Darstellung nach rechts oder links bzw. oben oder unten verschieben.
Ein Trigger (Source, Condition, Level) sorgt für ein stehendes Bild.

Messung

Kapazität

	f	20 kHz	50 kHz	10 kHz
C3	U	2.6 V	1.74 V	2.9 V
M2	I	15 mA	24.6 mA	8.3 mA

Je höher die Frequenz, desto kleiner der Widerstand.

\( \frac{U}{I} = \frac{1}{\omega C} \)
\( \frac{\underline{U}}{\underline{I}} = \frac{1}{j \omega C} = \underline{Z}_C \)

Induktivität

	f	20 kHz	50 kHz	10 kHz
C4	U	2.72 V	2.95 V	2.2 V
M1	I	10.54 mA	4.79 mA	17.48 mA

Je höher die Frequenz, desto größer der Widerstand.

\( \frac{\underline{U}}{\underline{I}} = j \omega L = \underline{Z}_L \)

Messung mit R, L und C und Zeigerdiagramm

Stellen Sie die Spannungen, Ströme und Widerstände mit Zeigern dar.

Zeitabhängige Gleichungen:
\( u(t) = \hat{u} sin(\omega t + \phi_u ) \)
\( i(t) = \hat{i} sin(\omega t + \phi_i ) \)
Ohmsches Gesetz: U = I * R

Die Amplituden liest man unter Measurement ab. 1 Kästchen soll 1 cm entsprechen (Normierung).
(C2) uR = 1.5 V
(M3) iR = 15 mA
(C3) uC = 2.62 V
(M2) iC = 14.8 mA
(C4) uL = 2.76 V
(M1) iL = 10.1 mA

Phasenverschiebung bei t = 0 s.
Eine Periode, 5 Kästchen a 10 us = 50 us entspricht 2 π oder 360°.
\( y(t) = \hat{y} cos(\omega t + \phi_y \)
Die Phasen ergeben sich dann zu:
(C2)φ_UR = 3/10 * 180° = 54°
(M3)φ_IR = 3/10 * 180° = 54°
(C3) φ_UC = 1/10 * 180° = 18°
(M2)φ_IC = 6/10 * 180° = 108°
(C4)φ_UL = 4/10 * 180° = 72°
(M1)φ_IL = -1/10 * 180° = -18°

Idealer Ohmscher Zweipol

u = R i

\( \hat{u} cos(\omega t + \phi_{u}) = R \hat{i} cos(\omega t + \phi_{i}) \)
\( \hat{u} = R \hat{i} \)
φ_u = φ_i
φ_R = φ_u - φ_i = 0°
Strom und Spannung sind in Phase

Leistung

Wirkleistungsschwingung

Komplexe Symbole

\( U \underline{/\phi_U} = R I \underline{/\phi_I} \)
\( \underline{U} = R \underline{I} \)
\( \underline{Z}_R = R \)
\( \underline{Y}_R = \frac{1}{R} = G \)

Idealer Ohmscher Zweipol

Electronic Explorer
Bild Aufbau, i(t), u(t), p(t) Oszilloskop

Komplexe Leistung des idealen Ohmschen Zweipols

\( \underline{S}_R = \underline{Z}_R I^2 = R I^2 \)

\( \underline{S}_R = \underline{Y}_R^{*} U^2 = G U^2 \)

Wirkleistung
φ_R = 0
Scheinleistung = Wirkleistung
\( \underline{S}_R = P_R = U I \)

Zeigerdiagram Farblich U, I, Z, Y

Zeiger in der komplexen Ebene dienen der Veranschaulichung der komplexen Rechnung.
Zur Zeichnung muss jede Größe normiert werden.
z.B. 1 V, 1 A, 1 Ohm entspricht 1cm,

Induktivität

Differentialgleichung

\( u_{L} = L \frac{d I}{d t} \)

\( i(t) = \hat{i} cos(\omega t + \phi_i) \)

\( \hat{u} cos(\omega t + \phi_u) = - \omega L \hat{i} sin(\omega t + \phi_i) \)

\( \hat{u} cos(\omega t + \phi_u) = \omega L \hat{i} cos(\omega t + \phi_i + \frac{\pi}{2} ) \)

\( \hat{u} = \omega L \hat{i} \)

\( \phi_u = \phi_i + \frac{\pi}{2} \)

Komplexer Widerstand

\( \underline{u}(t) = \hat{u} e^{j(\omega t + \phi_{u})} \)

\( \underline{Z} = j \omega L \)

Komplexes Ohmsches Gesetz

\( \underline{U} = j \omega L \underline{I}\)

An einem idealen induktiven Zweipol L eilt die Sinusspannung dem Sinusstrom um den Winkel 90° vor.
Effektivwert: U = ω L I

Leistungsschwingung Induktivität

P = S cosφ_L
Reine Blindleistungsschwingung

Mittelwert 0
Amplitude Q

Passiver Zweipol

Energiespeicher der Leistung in einer Halbperiode aufnimmt und dann wieder abgibt.

Energieberechnung

\( W_{max} = \frac{1}{2} L \hat{i}^2 = L I^2 \)
Effektivwert des Stromes

Oszilloskop u(t), i(t), p(t)

Komplexer Widerstand L Induktivität

\( \underline{U} = j \omega L \underline{I} \)
\( U \underline{/\phi_u} = \omega L I \underline{/\phi_i + 90 °} \)
Komplexer Widerstand
\( \underline{Z}_L = j \omega L \)
X_L = ω L
Leistung
\( \underline{S} = P + jQ = \underline{Z}_L I^2 = j \omega L I^2 \)
Q_L = X_L I^2
Blindleistung positiv: Q_L > 0
Q = S = U I

Zeigerdiagram Farblich U, I, Z, Y

Beispiel Induktivität

Ein idealer Zweipol L = 24 mH liegt an der Sinusspannung U = 10V; f = 800 Hz.
Wir wollen den komplexen Widerstand, den komplexen Leitwert sowie den Strom und die Blindleistung berechnen.

Kapazität

\( C = \frac{Q}{U} = \frac{I t }{U} \)

Differentialgleichung

\( i_{C} = C \frac{d U}{d t} \)

\( u(t) = \hat{u} cos(\omega t + \phi_u) \)

\( \hat{i} cos(\omega t + \phi_i) = - \omega C \hat{u} sin(\omega t + \phi_u) \)

\( \hat{i} cos(\omega t + \phi_i) = \omega C \hat{u} sin(\omega t + \phi_u + \frac{\pi}{2}) \)

\( \hat{i} = \omega C \hat{u} \)

\( \phi_i = \phi_u + \frac{\pi}{2} \)

An einem idealen kapazitiven Zweipol C eilt der Sinusstrom der Sinusspannung um den Winkel 90° vor.
Effektivwert: I = ω C U

Komplexer Widerstand

\( \underline{u}(t) = \hat{u} e^{j(\omega t + \phi_{u})} \)

\( \underline{Z} = \frac{1}{j \omega C} \)

Komplexes Ohmsches Gesetz

\( \underline{U} = \frac{\underline{I}}{j \omega C} \)

Leistungsschwingung Kapazität

P = S cos φ_C
Reine Blindleistungsschwingung

Mittelwert 0
Amplitude Q

Passiver Zweipol

Energiespeicher der Leistung in einer Halbperiode aufnimmt und dann wieder abgibt.

Energieberechnung

\( W_{max} = \frac{1}{2} C \hat{u}^2 = C U^2 \)
Effektivwert der Spannung

Oszilloskopbild u(t), i(t), p(t)

Komplexer Widerstand C Kapazität

\( \underline{U} = \frac{1}{j \omega C} \underline{I} \)
\( U \underline{/\phi_i} = \frac{1}{\omega C} I \underline{/\phi_i - 90 °} \)
Komplexer Widerstand
\( \underline{Z}_C = \frac{1}{j \omega C} \)
\( X_{L} = \frac{1}{\omega C} \)
Leistung
\( \underline{S} = P + jQ = \underline{Y}_C^* U^2 = - j \omega C U^2 \)
Q_C = - Y_C U²
Blindleistung negativ: Q_C < 0
Q = - S = - U I

Zeigerdiagram Farblich U, I, Z, Y

Beispiel Kapazität

An einem Kondensator wird an einer Wechselspannung 5 V ( f = 10 kHz) der Strom 80 mA gemessen.
Wir wollen den komplexen Widerstand, den komplexen Leitwert, die Kapazität sowie die Blindleistung berechnen.

Zusammenfassung und nächstes Mal

Komplexer Widerstand und Leitwert von C und L
\( \underline{Z}_C = \frac{1}{j\omega C} \)
\( \underline{Z}_L = j \omega L \)
Zeigerdiagramme
Leistung, Wirkleistung, Blindleistung
\( \underline{S}_C = - j \omega C U^2 \)
\( \underline{S}_L = j \omega L I^2 \)

10 Reihenschaltung

2022 GET 2 09 Induktivität und Kapazität Prof. Dr. Joerg Vollrath

Grundlagen Elektrotechnik 2 (GET2)

09 Induktivität und Kapazität

Prof. Dr. Jörg Vollrath

Video der 19. Vorlesung 8.6.2021

Rückblick und Übersicht

Leistung

Grundzweipole

Ziele

Messung mit R, L und C bei 20 kHz

Spannungen und Widerstände werden mit komplexen Symbolen dargestellt.

Fragen:

Oszilloskop

Messung

Messung mit R, L und C und Zeigerdiagramm

Stellen Sie die Spannungen, Ströme und Widerstände mit Zeigern dar.

Idealer Ohmscher Zweipol

u = R i

Leistung

Komplexe Symbole

Komplexe Leistung des idealen Ohmschen Zweipols

Induktivität

Differentialgleichung

Komplexer Widerstand

Komplexes Ohmsches Gesetz

Leistungsschwingung Induktivität

Komplexer Widerstand L Induktivität

Beispiel Induktivität

Kapazität

Differentialgleichung

Komplexer Widerstand

Komplexes Ohmsches Gesetz

Leistungsschwingung Kapazität

Komplexer Widerstand C Kapazität

Beispiel Kapazität

Zusammenfassung und nächstes Mal