Grundlagen Elektrotechnik 2 (GET2)

10 Reihenschaltung

Prof. Dr. Jörg Vollrath

Rückblick und Übersicht

Ohmscher Widerstand	\( \underline{U} = R \underline{I} \)	\( \underline{Z} = R \)	P = R I²	Q = 0
Induktivität, Spule	\( \underline{U} = j \omega L \underline{I} \)	\( \underline{Z} = j \omega L \)	P = 0	Q = ω L I² > 0
Kapazität	\( \underline{U} = \frac{1}{j \omega C} \underline{I} \)	\( \underline{Z} = \frac{1}{j \omega C} \)	P = 0	Q = - ω C U² < 0

Reihenschaltung
R L, R C, \( \underline{Z}_1 \underline{Z}_2 \)
Spannungsteiler

P und Q sind reelle Zahlen, \( \underline{S} \) ist komplex.

Reihenschaltung von R und L: Ersatzschaltbild

Beide Zweipole werden vom selben Strom durchflossen
\( \underline{U}_R = R \underline{I} \)
\( \underline{U}_L = j \omega L \underline{I} \)
\( \underline{U} = \underline{U}_R + \underline{U}_L = R \underline{I} + j \omega L \underline{I} \)
\( \underline{Z}_e = R_e + j X_e = R + j \omega L \)
Wirkwiderstand R_e = R
Scheinwiderstand
\( Z_e = \sqrt{R^2 + (\omega L)^2} \)

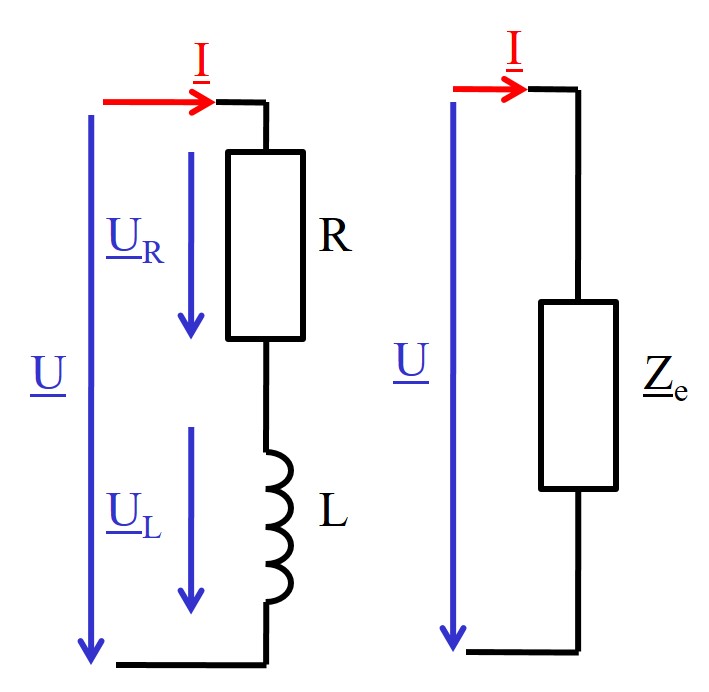
Reihenschaltung von R und L: Zeigerdiagramm

\( \underline{U} = \underline{U}_R + \underline{U}_L = R \underline{I} + j \omega L \underline{I} \)
\( \underline{Z}_e = R_e + j X_e = R + j \omega L \)
Wirkwiderstand R_e = R
Scheinwiderstand
\( Z_e = \sqrt{R^2 + (\omega L)^2} \)
\( \phi_z = atan \frac{\omega L}{ R}\)
Bereich der Phasenverschiebung 0 < φ < 90°
Blindwiderstand und Blindleistung positiv
Spule für niedrige Frequenzen Reihenschaltung R und L

Beispiel R und L

Eine Reihenschaltung aus den idealen Zweipolen R = 16 Ω und L = 38,2 mH wird von einem Sinusstrom 0.5 A (f=50Hz) durchflossen.
Wir wollen die Klemmenspannung, die Teilspannungen und den Phasenverschiebungswinkel berechnen. Außerdem wollen wir den komplexen Widerstand der Reihenschaltung ermitteln.

Test Ersatzquelle

Eine ideale Sinusspannungsquelle mit der Quellenspannung \( U_1 = 5 V \underline{/0°} \) wird mit einem Widerstand \( R_1 = 20 \Omega \) und einer Kapazität \( C_1 = 500 nF \) beschaltet.
Berechnen und zeichnen Sie die äquivalente Spannungsquelle und äquivalente Stromquelle bei 40 kHz.

Reihenschaltung von R und C: Ersatzschaltbild (15.4.2025)

Beide Zweipole werden vom selben Strom durchflossen
\( \underline{U}_R = R \underline{I} \)
\( \underline{U}_C = \frac{1}{j \omega C} \underline{I} \)
\( \underline{U} = \underline{U}_R + \underline{U}_C = R \underline{I} - \frac{j}{ \omega C} \underline{I} \)
\( \underline{Z}_e = R_e + j X_e = R - j \frac{1}{\omega C} \)
Wirkwiderstand R_e = R
Scheinwiderstand
\( Z_e = \sqrt{R^2 + \frac{1}{(\omega C)^2}} \)

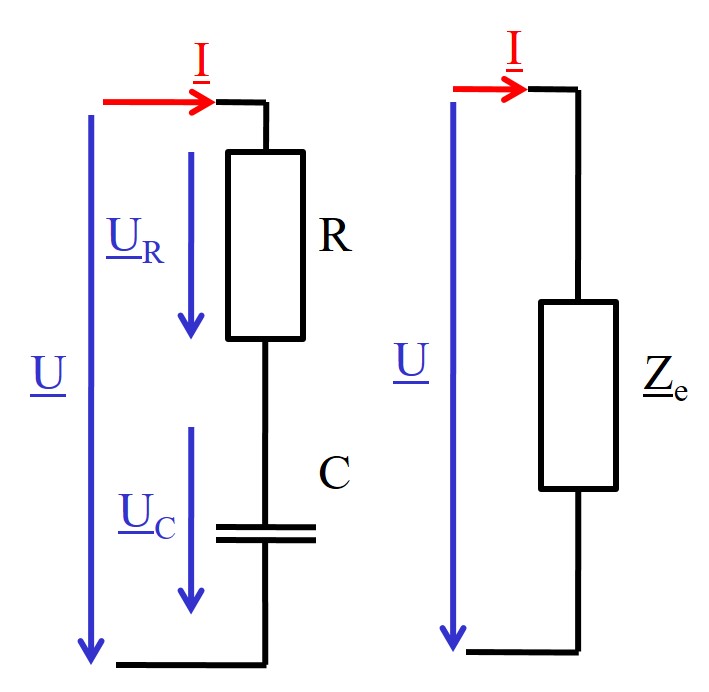
Reihenschaltung von R und C: Zeigerdiagramm

\( \underline{U} = \underline{U}_R + \underline{U}_C = R \underline{I} - j \frac{1}{\omega C} \underline{I} \)
\( \underline{Z}_e = R_e + j X_e = R - j \frac{1}{\omega C} \)
Wirkwiderstand R_e = R
Scheinwiderstand
\( Z_e = \sqrt{R^2 + \frac{1}{(\omega C)^2}} \)
\( \phi_z = atan \left( - \frac{1}{ \omega C R} \right) \)
Bereich der Phasenverschiebung -90° < φ < 0°
Blindwiderstand und Blindleistung negativ

Reihenschaltung komplexe Widerstände

Lineare passive Zweipole
\( \underline{Z}_1 = R_1 + j X_1 \)
\( \underline{Z}_2 = R_2 + j X_2 \)
\( \underline{Z}_e = \underline{Z}_1 + \underline{Z}_2 \)
\( \underline{Z}_e = (R_1 + R_2) + j (X_1 + X_2) \)
\( \underline{Z}_e = R_e + j X_e \)
X_e < 0 kapazitiv
X_e > 0 induktiv
\( \underline{Z}_e = \sum_{k=1}^n \underline{Z}_k \)
\( \underline{Z}_e= \sum_{k=1}^n R_k + j \sum_{k=1}^n X_k \)

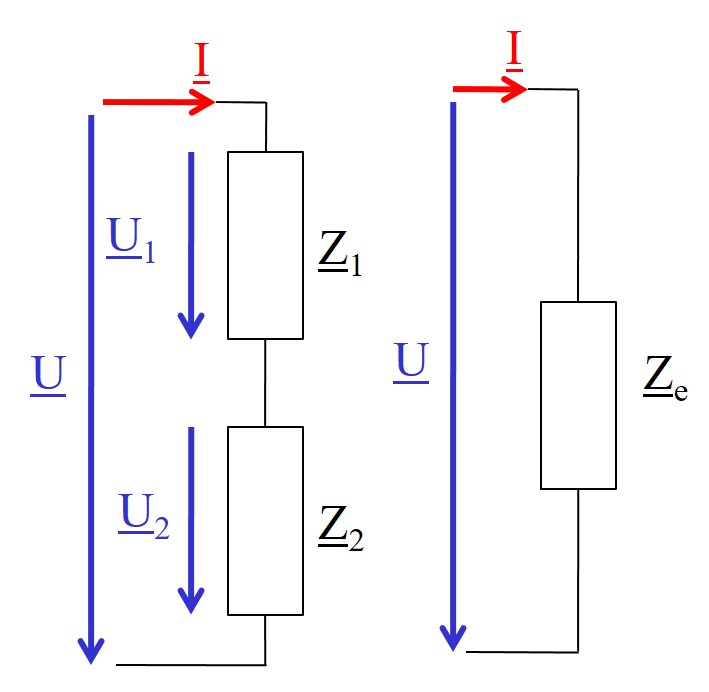
Komplexe Leistung einer Reihenschaltung

Summe der Teilleistungen
\( \underline{S}_1 = P_1 + j Q_1 \)
\( \underline{S}_2 = P_2 + j Q_2 \)
\( \underline{S} = \underline{U} \cdot \underline{I}^* = (\underline{U}_1 + \underline{U}_2 ) \cdot \underline{I}^* = \underline{S}_1 + \underline{S}_2 \)
\( \underline{S} = (P_1 + P_2) + j (Q_1 + Q_2) \)
\( \underline{S} = \sum_{k=1}^n \underline{S}_k = \sum_{k=1}^n P_k + j \sum_{k=1}^n Q_k \)

Beispiel Komplexe Leistung einer Reihenschaltung

Wir wollen den Ersatzzweipol der Reihenschaltung von \( \underline{Z}_1 = 15.6 \Omega \underline{/39.8°}\) und \( \underline{Z}_2 = 17 \Omega \underline{/-62°}\) berechnen, sowie die Leistungen, die an 15 V Sinusspannung (f = 400 Hz) entstehen.
Wie gross sind die verwendeten Widerstände, Kapazitäten und Induktivitäten?

Einfache Kapazitätsmessung

Sinusspannungsquelle mit Amplitude \( \hat{u} \) und konstanter Frequenz f
Wechselstrommesser misst \( \hat{i} \)
Kapazitätsberechnung mit Hilfe des komplexen Widerstandes der Kapazität

\( C = \frac{I}{2 \pi f U} \)
Diskussion: Messbereich, Messabweichungen
Präszisionsmessungen: Messbrücken!?

Spannungsteilerregeln

Die Spannungsteilerregel der Gleichstromtechnik gilt auch für die Wechselstromnetze im komplexen

\( \underline{I} = \frac{\underline{U}_1}{\underline{Z}_1} = \frac{\underline{U}}{\underline{Z}} \)

\( \frac{\underline{U}_1}{\underline{U}} = \frac{\underline{Z}_1}{\underline{Z}} \)

Spulenmessung

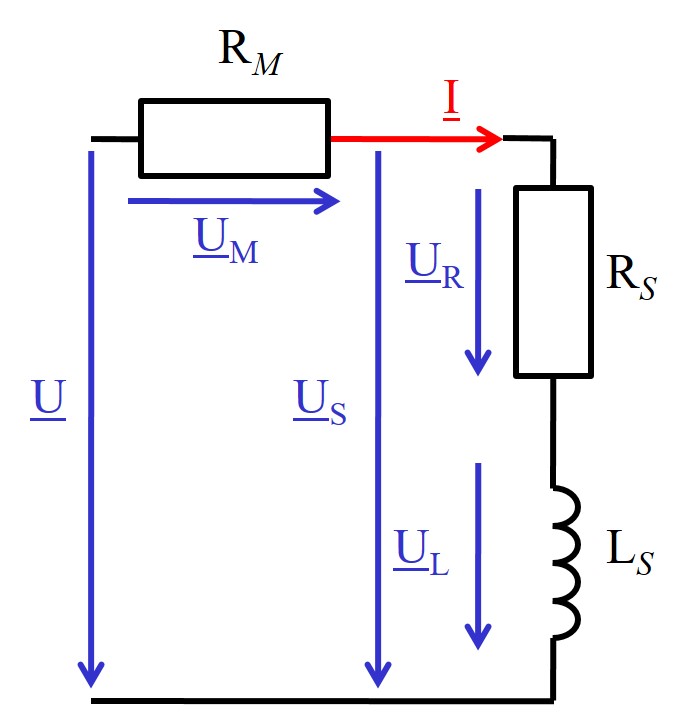
Zur Bestimmung der Werte einer Spulenersatzschaltung kann das Dreispannungsmesser-Verfahren angewendet werden. Dabei wird die Spule in Reihenschaltung mit einem bekannten Widerstand RM an Sinusspannung betrieben.
Die Effektivwerte der Spannungen U, UM und Us werden gemessen; damit kann man die gesuchten Größen RS und LS berechnen.

Name des Verfahrens: Messung von 3 Spannungen

Beispiel: Spulenmessung

R_M = 27 Ω, f = 50 Hz, U_M = 5.4 V, U_S = 6.0 V, U = 10.2 V
Gesuchten Größen: R_S und L_S

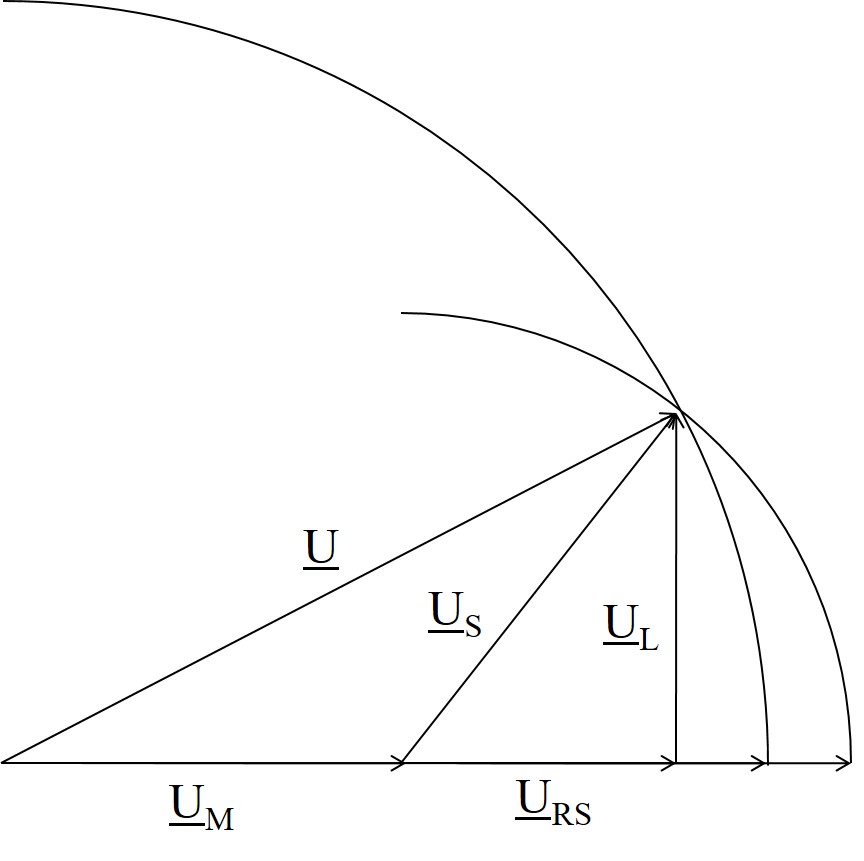
Spulenmessung Rechnung (22.04.2025)

Gesuchten Größen: R_S und L_S

(1) \( \underline{U} = (R_M + R_S + j \omega L) \underline{I} \)
(2) \( \underline{U}_M = R_M \underline{I} \)
(3) \( \underline{U}_S = (R_S + j ω L) \underline{I} \)

Effektivwerte:

(4) aus (1) \( U = \sqrt{((R_M + R_S)^2+ (\omega L)^2)} I \)
(5) aus (2) U_M = R_M I
(6) aus (3) \( U_S = \sqrt{(R_S^2 + (\omega L)^2)} I \)

3 Gleichungen 3 unbekannte I, R_S,L
Umformen: I wird eliminiert:

(7) aus (4),(5) \( (R_M + R_S)^2 + (\omega L)^2 = \left( \frac{U \cdot R_M}{U_M} \right)^2 \)
(8) aus (6),(5) \( R_S^2 + (\omega L)^2 = \left( \frac{U_S R_M}{U_M} \right)^2 \)

(9) umgeformt (8) \( (\omega L)^2 = \left( \frac{U_S R_M}{U_M} \right)^2 - R_S^2 \)
(10) (9) in (7) \( (R_M + R_S)^2 + \left( \frac{U_S R_M}{U_M} \right)^2 - R_S^2 = \left( \frac{U R_M}{U_M} \right)^2 \)
Jetzt kann (10) nach R_S umgeformt werden:
(11) \( R_M^2 + 2 R_M R_S + R_S^2 + \left( \frac{U_S R_M}{U_M} \right)^2 - R_S^2 = \left( \frac{U R_M}{U_M} \right)^2 \)
(12) \( 2 R_M \cdot R_S = \left( \frac{U R_M}{U_M} \right)^2 - R_M^2 - \left( \frac{U_S R_M}{U_M} \right)^2 \)
(13) \( R_S = \frac{1}{2 R_M} \left[ \left( \frac{U R_M}{U_M} \right)^2 - R_M^2 - \left( \frac{U_S R_M}{U_M} \right)^2 \right] \)
\( R_S = \frac{R_M}{2} \left[ \left( \frac{U}{U_M} \right)^2 - 1 - \left( \frac{U_S}{U_M} \right)^2 \right] = 18 \Omega \)
Aus 9 umgeformt nach L
\( L = \frac{1}{\omega} \sqrt{\left( \frac{U_S R_M}{U_M} \right)^2 - R_S^2} = 76.4 mH \)

Nachdenken über die Lösung

Liste der gegebenen Größen
Liste der gesuchten Größen
Annahme: Reihenschaltung der Strom ist überall gleich
Lösungsweg: Zeigerdiagramm
Lösungsweg: Rechnung
3 Gleichungen mit 3 unbekannten -> Lösbar
Größe R, L ok? Realistisch?

Beispiel mit Electronic Explorer

Zusammenfassung und nächstes Mal

Reihenschaltung genauso im komplexen für AC wie für DC
Widerstandsaddition

\( \underline{Z} = \underline{Z}_1 + \underline{Z}_2 \)
Spannungsteiler
Leistungsaddition

11 Parallelschaltung

2022 GET 2 10 Reihenschaltung Prof. Dr. Joerg Vollrath