Grundlagen Elektrotechnik 2 (GET2)

11 Parallelschaltung

Prof. Dr. Jörg Vollrath

Rückblick und Übersicht

Reihenschaltung, Widerstände, Addition, Spannungsteiler, Leistung
Messanwendungen
Parallelschaltung, Leitwerte, Stromteiler, leistung

Parallelschaltung passiver Zweipole

Es werden Leitwerte verwendet.
Die Spannung ist an beiden komplexen Grundzweipolen gleich.
\( \underline{I} = \underline{I}_R + \underline{I}_C \)

\( \underline{I} = \frac{\underline{U}}{R} + \frac{\underline{U}}{\frac{1}{j \omega C}} \)

\( \underline{I} = G \cdot \underline{U} + j \omega C \underline{U} \)

\( \underline{I} = \left( G + j \omega C \right) \underline{U} \)

\( \underline{Y}_R = G \), \( \underline{Y}_C = j \omega C \)

\( \underline{Y}_e = \underline{Y}_R + \underline{Y}_C = G + j \omega C = G_e + j B_e \)

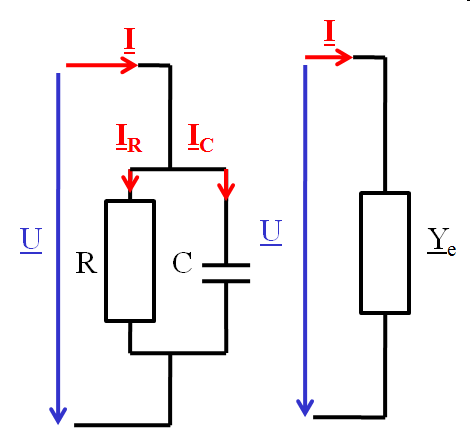Komplexe Zeiger Parallelschaltung

Leitwert des Ersatzzweipols
\( \underline{Y}_e = G_e + j B_e = G + j \omega C \)
Scheinleitwert
\( Y_e = \sqrt{G^2 + (\omega C )^2} \)
Winkel φ
\( \phi = arctan \frac{\omega C}{G} \)
Phasenverschiebung
-90° < φ < 0°
Blindwiderstand und Blindleistung negativ
Kapazitive Blindleistung

Beispiel Parallelschaltung

Eine Parallelschaltung aus den Grundzweipolen R = 50 Ω und L = 10 mH liegt an der Sinusspannung U = 20 V (400 Hz). Wir wollen den komplexen Leitwert der Schaltung und den Gesamtstrom berechnen.

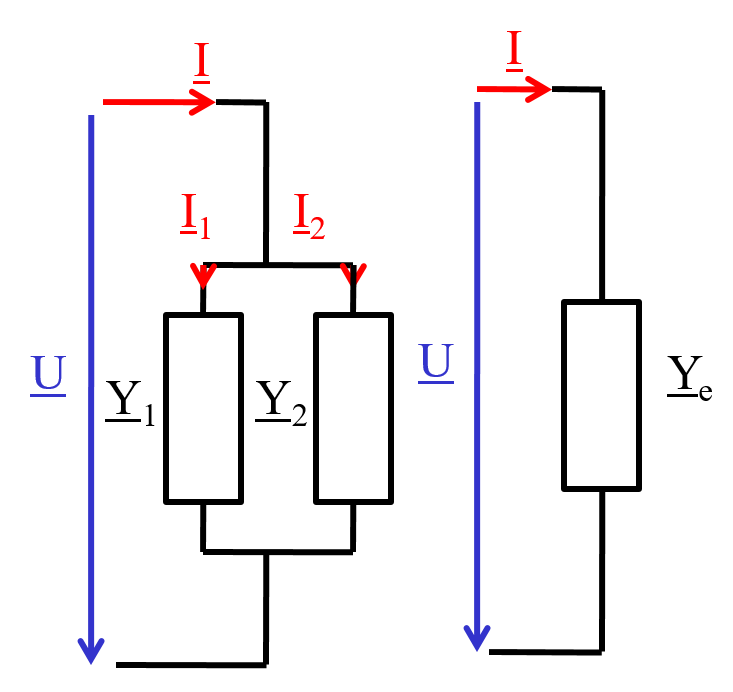
Parallelschaltung komplexer Leitwerte

\( \underline{I} = \underline{I}_1 + \underline{I}_2 \)

\( \underline{Y}_e = \underline{Y}_1 + \underline{Y}_2 \)

\( \underline{Y}_e = G_1 + G_2 + j ( B_1 + B_2) \)

\( \underline{Y} = \sum_{k=1}^n \underline{Y}_k = \sum_{k=1}^n G_k + j \sum_{k=1}^n B_k \)

Komplexe Leistung

Wirkleistung: P = G_e U²
Blindleistung: Q = - B_e U²

\( \underline{S} = \sum_{k=1}^n \underline{S}_k = \sum_{k=1}^n P_k + j \sum_{k=1}^n Q_k \)

Wirkleitwert: G
Blindleitwert: B

Stromteilerregel

\( \underline{U}_e = \frac{\underline{I}_e}{\underline{Y}_e} = \frac{\underline{I}_1}{\underline{Y}_1} = \frac{\underline{I}_2}{\underline{Y}_2}\)

\( \frac{\underline{I}_1}{\underline{I}_e} = \frac{\underline{Y}_1}{\underline{Y}_e} \)

Test: Komplexer Widerstand

Bestimmen Sie den komplexen Widerstand der folgenden Schaltung allgemein (ωL = 2 R₁), für ω=0 und ω->∞ für R = R1 = 2R₂.
Stellen Sie Spannungen, Ströme, Widerstände und Leitwerte im Zeigerdiagramm dar.

WiderRLRTest.asc

Version 4
SHEET 1 880 680
WIRE 224 64 112 64
WIRE 272 64 224 64
WIRE 384 64 352 64
WIRE 224 80 224 64
WIRE 384 80 384 64
WIRE 224 176 224 160
WIRE 224 176 112 176
WIRE 256 176 224 176
WIRE 384 176 384 160
WIRE 384 176 256 176
WIRE 256 192 256 176
FLAG 256 192 0
FLAG 112 64 U
SYMBOL res 240 176 R180
WINDOW 0 36 76 Left 2
WINDOW 3 36 40 Left 2
SYMATTR InstName R1
SYMATTR Value 10k
SYMBOL ind 368 48 R90
WINDOW 0 5 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName L1
SYMATTR Value 31.8m
SYMBOL res 368 64 R0
SYMATTR InstName R2
SYMATTR Value 5k
TEXT 104 112 Left 2 ;U
TEXT 104 208 Left 2 !.tran 30u
TEXT 104 240 Left 2 !VU U 0 SINE(0 10 100k) AC 1
TEXT 400 216 Left 2 !;ac dec 10 1 10000k
LINE Normal 128 160 128 80
LINE Normal 128 160 112 144
LINE Normal 144 144 128 160

Beispiel Parallelschaltung (02.05.2023)

Wir wollen den Strom I, die Wirkleistung und die Blindleistung sowie den Leistungsfaktor der Parallelschaltung berechnen
R₁ = 50 Ω, R₂ = 20 Ω, L₁ = 100 mH, C₁ = 20 µF, U = 230 V, f = 50 Hz.

BspWiderCRL.asc

Version 4
SHEET 1 880 680
WIRE 192 16 128 16
WIRE 304 16 192 16
WIRE 400 16 304 16
WIRE 304 48 304 16
WIRE 192 96 192 16
WIRE 400 96 400 16
WIRE 304 160 304 128
WIRE 192 272 192 160
WIRE 192 272 128 272
WIRE 304 272 304 240
WIRE 304 272 192 272
WIRE 400 272 400 176
WIRE 400 272 304 272
WIRE 192 304 192 272
FLAG 192 304 0
FLAG 128 16 U
SYMBOL cap 176 96 R0
SYMATTR InstName C1
SYMATTR Value 20�
SYMBOL res 288 32 R0
SYMATTR InstName R2
SYMATTR Value 20
SYMBOL ind 288 144 R0
SYMATTR InstName L1
SYMATTR Value 100m
SYMBOL res 384 80 R0
SYMATTR InstName R1
SYMATTR Value 50
TEXT 96 136 Left 2 ;U
TEXT 224 304 Left 2 !VU U 0 SINE(0 230 50)
TEXT 224 336 Left 2 !.tran 100m
LINE Normal 128 256 112 240
LINE Normal 144 240 128 256
LINE Normal 128 48 128 256

Umrechnung zwischen Widerstand und Leitwert

\( \underline{Z} = R + j X \)

\( \underline{Y} = \frac{1}{\underline{Z}} = \frac{1}{R + j X} = \frac{1}{R + j X} \frac{R - j X}{R - j X} = \frac{R}{R^2 + X^2} - \frac{j X}{R^2 + X^2} \)

\( \underline{Y} = \frac{R}{R^2 + X^2} - \frac{j X}{R^2 + X^2} = G + jB \)

\( \underline{Z} = \frac{G}{G^2 + B^2} - \frac{j B}{G^2 + B^2} = R + jX \)

Beispiel Parallelschaltung

Berechnung von R_e und X_e
R₁ = 10 kΩ, R₂ = 50 kΩ, L₁ = 2 mH, C₁ = 400 nF, f = 50 Hz,

WiderRLCR.asc

Version 4
SHEET 1 880 680
WIRE 144 64 112 64
WIRE 272 64 224 64
WIRE 384 64 352 64
WIRE 480 64 384 64
WIRE 480 80 480 64
WIRE 384 96 384 64
WIRE 256 176 112 176
WIRE 384 176 384 160
WIRE 384 176 256 176
WIRE 480 176 480 160
WIRE 480 176 384 176
WIRE 256 192 256 176
FLAG 256 192 0
FLAG 112 64 U
SYMBOL res 240 48 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 10k
SYMBOL ind 368 48 R90
WINDOW 0 5 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName L1
SYMATTR Value 2m
SYMBOL cap 368 96 R0
SYMATTR InstName C1
SYMATTR Value 400n
SYMBOL res 464 64 R0
SYMATTR InstName R2
SYMATTR Value 50k
TEXT 104 112 Left 2 ;U
TEXT 104 208 Left 2 !;tran 100m
TEXT 104 240 Left 2 !VU U 0 SINE(0 230 50) AC 1
TEXT 400 216 Left 2 !.ac dec 10 1 10000k
LINE Normal 128 160 128 80
LINE Normal 128 160 112 144
LINE Normal 144 144 128 160

Online Übungsportal

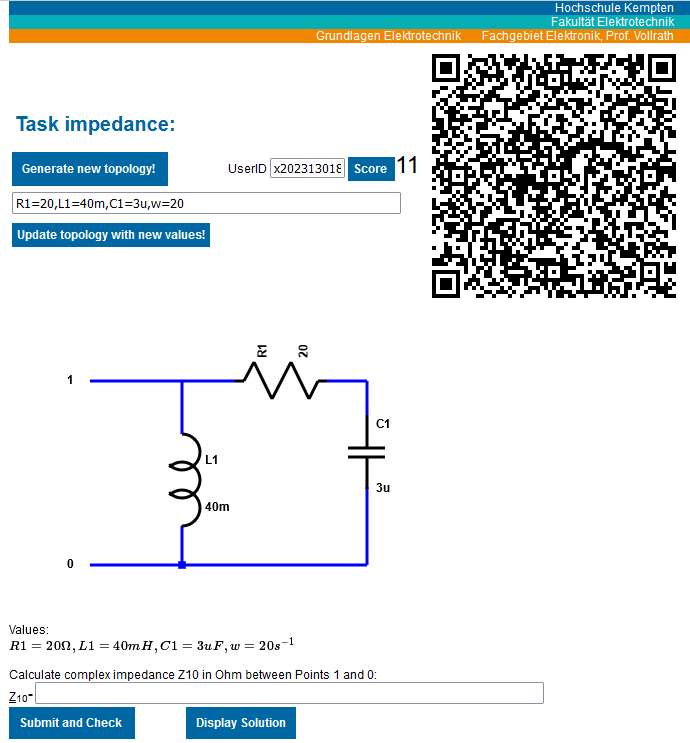
Die Elemente können mit dem Eingabefeld aktualisiert werden:
Eingabebeispiele: R1=20,L1=40m,C1=3u,w=20
L1=20m,R1=40,C1=6u,w=20
L1=40m,C1=3u,R1=20,w=20
Aktualisieren: Update topology with new values
Werte und Widerstandsart können veränderet werden.

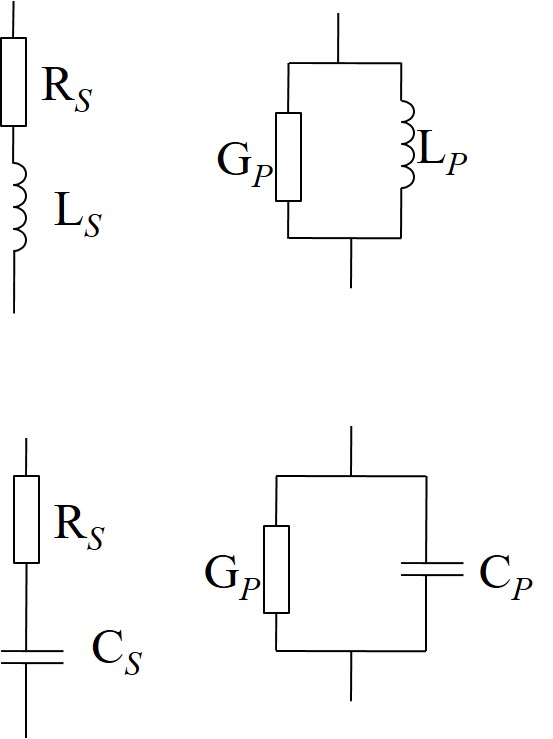
Reihen- und Parallel-Ersatzschaltung

Für den Widerstand \( \underline{Z} \) oder den Leitwert \( \underline{Y} \) kann man entweder eine Reihen- (Index S series) Ersatzschaltung oder eine Parallelersatzschaltung (Index P von parallel) angeben.
Gültig für eine Frequenz
Induktive Ersatzschaltbilder
Kapazitive Ersatzschaltbilder

Umwandlung einer Reihenschaltung in eine Parallelschaltung

Von einer Spule sind die Elemente der Reihen-Ersatzschaltung bekannt: R_s = 18 Ω; L_s = 76.4 mH
Wir wollen die Elemente der Parallel-Ersatzschaltung für f₁ = 50 Hz und für f₂ = 150 Hz berechnen.

Oszilloskop Tastkopf

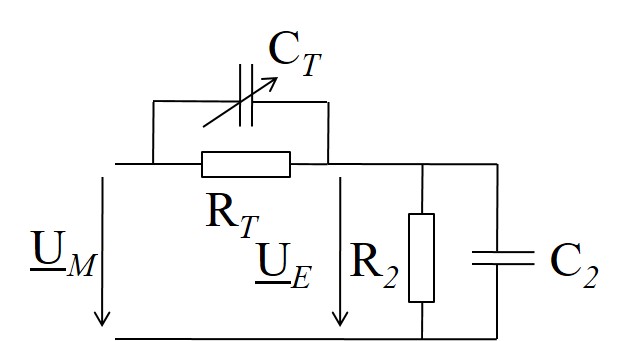
Der Eingangswiderstand eines Messgeräts kann mit einer Parallelschaltung einer Kapazität und eines Widerstandes modelliert werden. z.B. R₂ = 1 MΩ und C₂ = 25 pF.
Wenn die Eingangsimpedanz des Messgeräts zu niedrig oder die zu messende Spannung U_M zu hoch ist, kann ein Tastteiler verwendet werden; vielfach ist auch noch die Bezeichnung Tastkopf (probe) in Gebrauch.
Der Tastteiler besteht aus einem hochohmigen Widerstand R_T, dem ein einstellbarer Zylinderkondensator C_T zwischen den Elektroden A und B parallel geschaltet ist.
Das Spannungsteilungsverhältnis kann dann beim Abgleich frequenzunabhängig gemacht werden.

Feedback (30.04.2024)

Komplexer Widerstand und Leistung

Darstellung komplexer Größen mit Unterstrich
\( \underline{S} = \underline{U} \cdot \underline{I}^* = \underline{U} \frac{\underline{U}^*}{\underline{Z}^*} = \frac{U^2}{\underline{Z}^*}\)
Der konjugiert komplexe Strom wird durch konjugiert komplexe Spannung und konjugiert komplexem Widerstand dargestellt.
\( \underline{Z} = R + jX = R + j \omega L \)
X = ω L
P-Form \( \underline{Z} = Z \underline{/\phi_Z} \) zu R-Form \( \underline{Z} = R + j X \):
R = Z cos φ
X = Z sin φ
Nur bei einer Reihenschaltung gilt: \( S = I^2 R \)
Nur bei einer Parallelschaltung gilt: \( S = \frac{U^2}{R} \)
Zeichnen Sie ein Schaltbild

Zusammenfassung und nächstes Mal

Parallelschaltung, Zeigerdiagram, Leistung
Ersatzwiderstände
Seriell, parallel, Frequenzabhängigkeit

12 Resonanz

2022 GET 2 11 Parallelschaltung Prof. Dr. Joerg Vollrath

Grundlagen Elektrotechnik 2 (GET2)

11 Parallelschaltung

Prof. Dr. Jörg Vollrath

Video der 19. Vorlesung 8.6.2021

Rückblick und Übersicht

Parallelschaltung passiver Zweipole

Komplexe Zeiger Parallelschaltung

Beispiel Parallelschaltung

Parallelschaltung komplexer Leitwerte

Komplexe Leistung

Stromteilerregel

Test: Komplexer Widerstand

Beispiel Parallelschaltung (02.05.2023)

Umrechnung zwischen Widerstand und Leitwert

Beispiel Parallelschaltung

Online Übungsportal

Reihen- und Parallel-Ersatzschaltung

Umwandlung einer Reihenschaltung in eine Parallelschaltung

Oszilloskop Tastkopf

Feedback (30.04.2024)

Komplexer Widerstand und Leistung

Zusammenfassung und nächstes Mal