Grundlagen Elektrotechnik 2 (GET2)

12 Resonanz

Prof. Dr. Jörg Vollrath

11 Parallelschaltung

Übersicht

Begriff Resonanz
Reihen- und Parallelschwingkreis
Zeigerdiagramm
Resonanzüberhöhung

Schwingungsfähiges System

2 verschiedene Energiespeicher

Die Energie schwingt hin und her
Potentielle Energie der Masse, Federenergie

Feder-Masse-Pendel

Potenzielle Energie < - > kinetische Energie

Zweipoliges passives Netz mit L und C

Elektrische Energie schwingt hin und her
Elektrische Feldenergie
Magnetische Feldenergie

Schwingkreis (oscillation circuit)

Blindleistung von L und C gleiche Beträge
Klemmen Blindleistung=0
Resonanz (resonance)

Schwingkreis Electronic Explorer

Serienschwingkreis
Spule: Innenwiderstand 20 Ω
C = 45 nF, R = 53.3 Ω, L = 2.18 mH
\( f = \frac{1}{2 \pi \sqrt{C L } } = 16 kHz \)
\( K_U = \frac{1}{R} \sqrt{\frac{L}{C}} \)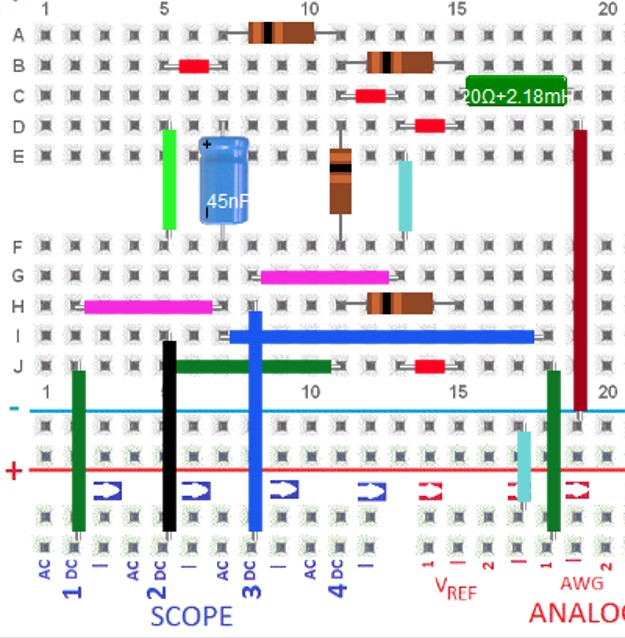

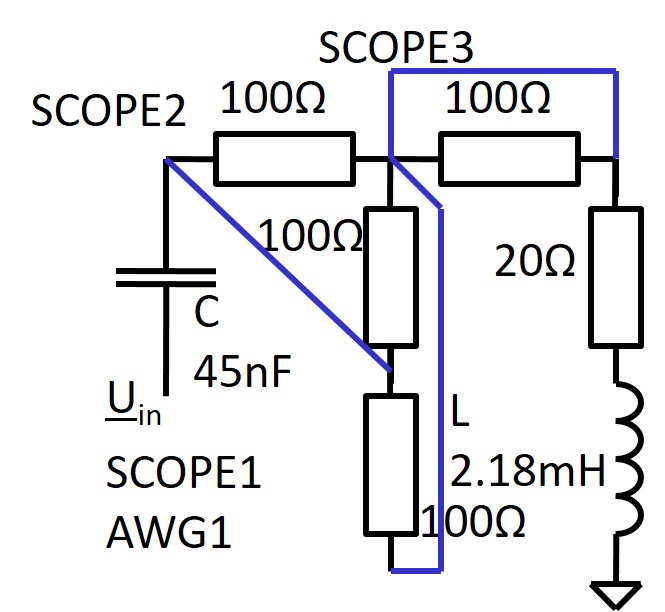
Schwingkreis LTSPICE

Serienschwingkreis
Spule: Innenwiderstand 20 Ω
C = 45 nF, R = 53.3 Ω, L = 2.18 mH
Resonanzfrequenz
\( f = \frac{1}{2 \pi \sqrt{C L } } = 16 kHz \)
Spannungsüberhöhung
\( K_U = \frac{1}{R} \sqrt{\frac{L}{C}} = 4.13 \)

Wenn U = 1 V mit 16 kHz anliegt, so hat die Spannung am Kondensator den Wert 4.13 V

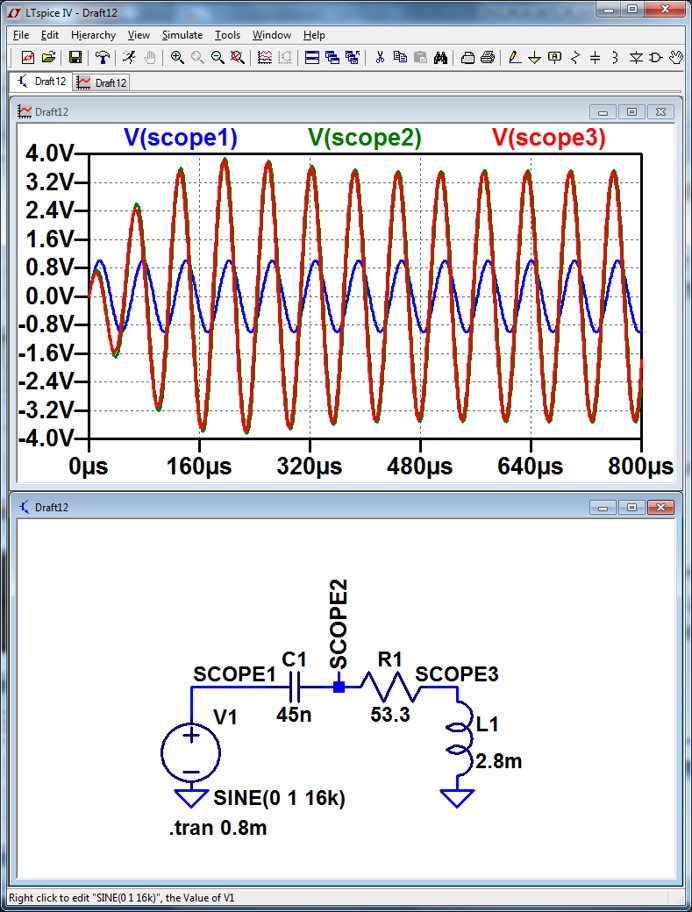
Nachdenken SPICE Simulation

Einschwingvorgang

Energietransfer
Schwingung an L und C wird größer

Spannung an Spule und Kapazität gegenphasig
Energie wird hin und her geschoben, Blindleistung

Der Widerstand R bestimmt den Strom -> Spannungsüberhöhung L und C bestimmen die Resonanzfrequenz und Spannungsüberhöhung

Reihenresonanz

Reihenschaltung R, L, C

Reihenschwingkreis (series oscillator circuit)

\( \underline{U} = \underline{U}_R + \underline{U}_L + \underline{U}_C \)
\( \underline{U} = R \underline{I} + j \omega L \underline{I} - j \frac{1}{\omega C} \underline{I} \)
\( \underline{Z} = R + j \omega L - j \frac{1}{\omega C} \)

3 Fälle:
(1) \( \omega L > \frac{1}{\omega C} \)
(2) \( \omega L = \frac{1}{\omega C} \)
(3) \( \omega L < \frac{1}{\omega C} \)

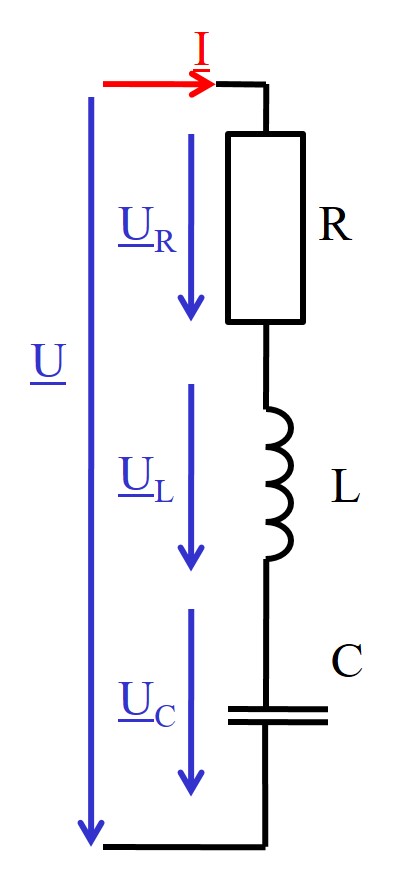
Zeigerdiagramm Reihenresonanz

Reihenschaltung R, L, C

Reihenschwingkreis (series oscillator circuit)

\( \underline{U} = \underline{U}_R + \underline{U}_L + \underline{U}_C \)
\( \underline{U} = R \underline{I} = j \omega L \underline{I} = - j \frac{1}{\omega C} \underline{I} \)
\( \underline{Z} = R + j \omega L - j \frac{1}{\omega C} \)

Resonanzfrequenz: (resonance frequency)

\( \omega L = \frac{1}{\omega C} \)

\( \omega = \frac{1}{\sqrt{C L}} \) \( f = \frac{1}{ \sqrt{2 \pi C L}} \)

Reihenresonanz Eigenschaften

Scheinwiderstand Z = R

Im{\( \underline{Z} \)} = 0
\( \underline{U} = \underline{U}_R \) in Phase mit \( \underline{I} \)
U = U_R
U_L = U_C
I ist bei Resonanzfrequenz am größten
Saugkreis
Spannungsüberhöhung K_U an C und L für:
U_L = U_C > U_R
\( K_U = \frac{U_C}{U} = \frac{\frac{I}{\omega C}}{I R} = \frac{1}{\omega C R } = \frac{1}{R} \sqrt{\frac{L}{C}} \)
\( K_U = \frac{U_L}{U} = \frac{I \omega L}{I R} = \frac{\omega L}{ R } = \frac{1}{R} \sqrt{\frac{L}{C}} \)
Achtung bei der Bauteildimensionierung

Reihenresonanz Leistung

Blindleistung Q

Q_L = X_L I² = ω L I²
\( Q_C = X_C I^2 = - \frac{1}{\omega C} I^2 \)
Q = Q_L + Q_C = 0
Die beiden Blindleistungen sind gegenphasig mit gleicher Amplitude
Abwechselnd wird die Energie in den Zweipolen L und C gespeichert

Wirkleistung P = S, \( \underline{S} \) ist reell

Beispiel Reihenschaltung

Eine Spule (R = 12 Ω, L = 35 mH) und ein Kondensator C = 1,0 µF sind in Reihe geschaltet. Wir wollen die Resonanzfrequenz und die Spannungsüberhöhung berechnen.

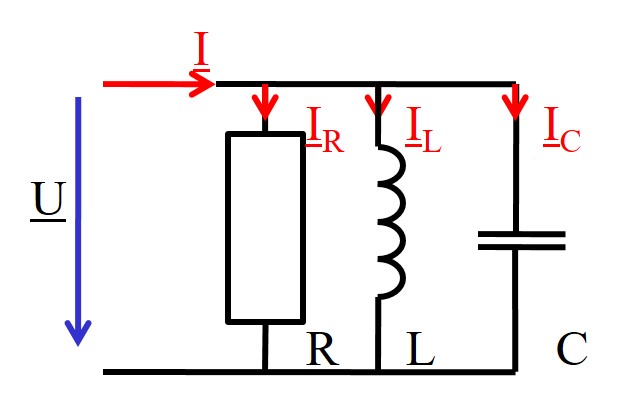
Parallelresonanz (03.05.2023)

Parallelschaltung R, L, C

Reihenschwingkreis (parallel oscillator circuit)

\( \underline{I} = \underline{I}_R + \underline{I}_L + \underline{I}_C \)
\( \underline{I} = \frac{1}{R} \underline{U} - j \frac{1}{\omega L} \underline{U} + j \omega C \underline{U} \)
\( \underline{Y} = \frac{1}{R} - j \frac{1}{\omega L} + j \omega C \)

3 Fälle:
(1) \( j \omega C > \frac{1}{\omega L} \)
(2) \( j \omega C = \frac{1}{\omega L} \)
(3) \( j \omega C < \frac{1}{\omega L} \)

Zeigerdiagramm Parallelresonanz

Parallelschaltung R, L, C

Reihenschwingkreis (parallel oscillator circuit)

\( \underline{U} = R \underline{I}_R = j \omega L \underline{I}_L = -j \frac{1}{\omega C} \underline{I}_C \)
I_C = I_L: Prallelresonanz
Resonanz: Y ist minimal (G), I = U Y ist minimal
Sperrkreis

Resonanzfrequenz:
(resonance frequency)

\( \omega_r = \frac{1}{\sqrt{C L}} \)

\( f_r = \frac{1}{\sqrt{ 2 \pi C L}} \)

Parallelresonanz Eigenschaften

Scheinwiderstand Z = R

Im{\( \underline{Z} \)} = 0
\( \underline{I} = \underline{I}_R \) in Phase mit \( \underline{U} \)
I = I_R
I_L = I_C
I ist bei Resonanzfrequenz am kleinsten
Sperrkreis
Stromüberhöhung K_I an C und L für:
I_L = I_C > I_R
\( K_I = \frac{I_C}{I_R} = \frac{ U \omega C}{\frac{U}{R}} = \omega C R = R \sqrt{\frac{C}{L}} \)
\( K_I = \frac{I_L}{I_R} = \frac{\frac{U}{\omega L}}{\frac{U}{R}} = \frac{ R }{\omega L} = R \sqrt{\frac{C}{L}} \)
Achtung bei der Bauteildimensionierung

Parallelresonanz Leistung

Blindleistung Q

\( Q_C = - Y_C U^2 = - \omega C I^2 \)
\( Q_L = Y_L U^2 = \frac{1}{\omega L} U^2 \)
Q = Q_L + Q_C = 0
Die beiden Blindleistungen sind gegenphasig mit gleicher Amplitude
Abwechselnd wird die Energie in den Zweipolen L und C gespeichert

Wirkleistung P = S, \( \underline{S} \) ist reell

Beispiel Zugbeeinflussung

Indusi

PZB

Zusammenfassung und nächstes Mal

In einem Netz mit mindestens einem Grundzweipol L und einem Grundzweipol C kann Resonanz auftreten

Bei der Resonanzfrequenz sind U und I in Phase.
Komplexer Widerstand Z und komplexer Leitwert Y sind reell

Reihen und Parallelschwingkreis sind Sonderfälle, bei denen nur jeweils ein Grundzweipol R, L und C vorhanden ist und R nicht die Resonanzfrequenz bestimmt.
Sind mehr Elemente vorhanden oder es besteht keine reine Reihen- oder Parallelschaltung

Kann die Resonanzfrequenz auch vom Grundzweipol R abhängen.
Kann es mehr als eine Resonanzfrequenz geben.

Für die Resonanzfrequenz gilt Im{\( \underline{Z} \)} = 0

13 Schwingkreis

2022 GET 2 12 Resonanz Prof. Dr. Joerg Vollrath