Grundlagen Elektrotechnik 2 (GET2)13 SchwingkreisProf. Dr. Jörg Vollrath12 Resonanz |

|
Video GET2 01 Einführung kompakt
Video der 19. Vorlesung 8.6.2021
|
Länge: 1:22:04 |
0:0:0 Evaluierung 0:0:0 Differenzverstärker 0:2:0 Eingangs und Ausgangswiderstand |
Wiederholung und Übersicht
- Schwingkreis: R, L, C
- Resonanz im Reihenschwingkreis
- Resonanz im Parallelschwingkreis
- Resonanzfrequenz
- Spannungs- und Stromüberhöhung
- Zugbeeinflussung
- Resonanz im gemischtes Netz
Übersicht
|
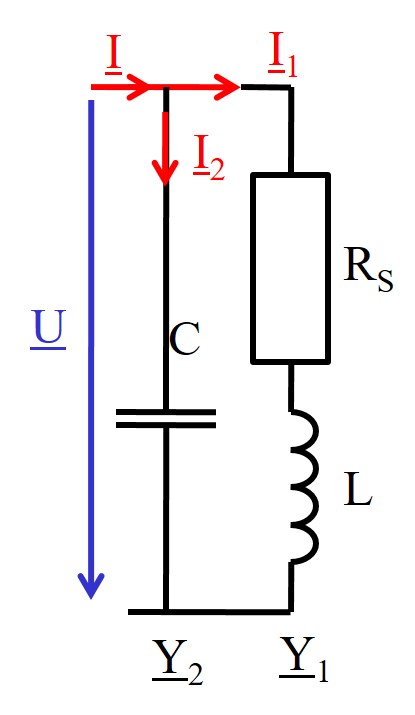 |
Widerstandstransformation und Resonanz
|
Zeigerdiagram für Resonanz (5.5.2025)
|
Start: \( \underline{U} \) und \( \underline{I} \) waagrecht. \( \underline{U}_Rs \) und \( \underline{U}_L \) senkrecht zueinander ergeben \( \underline{U} \). \( \underline{I} \) und \( \underline{I}_2 \) senkrecht zueinander. \( \underline{I}_1 \) und \( \underline{I}_2 \) ergeben \( \underline{I} \). |
Resonanzfrequenz
|
Beispiel Resonanzfrequenz
|
C = 0.5 uF; R = 147 Ω; L = 35 mH; Berechnen Sie die Resonanzfrequenz und den Wirkwiderstand bei Resonanzfrequenz.
\( f = \frac{1}{2 \pi} \sqrt{ \frac{1}{L C} - \left( \frac{R_S}{L} \right)^2 } = 1 kHz\)
RP > RS |
Übersicht (05.05.2025)
Grundelemente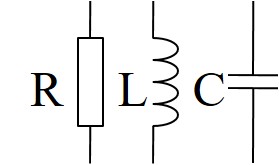
|
2 Grundelemente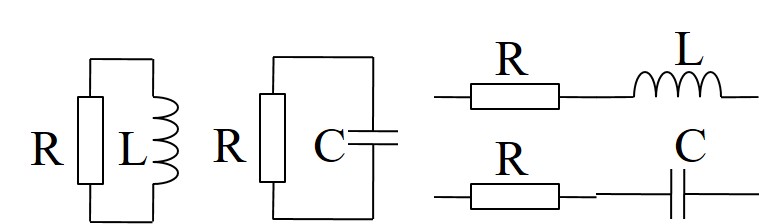
|
3 Grundelemente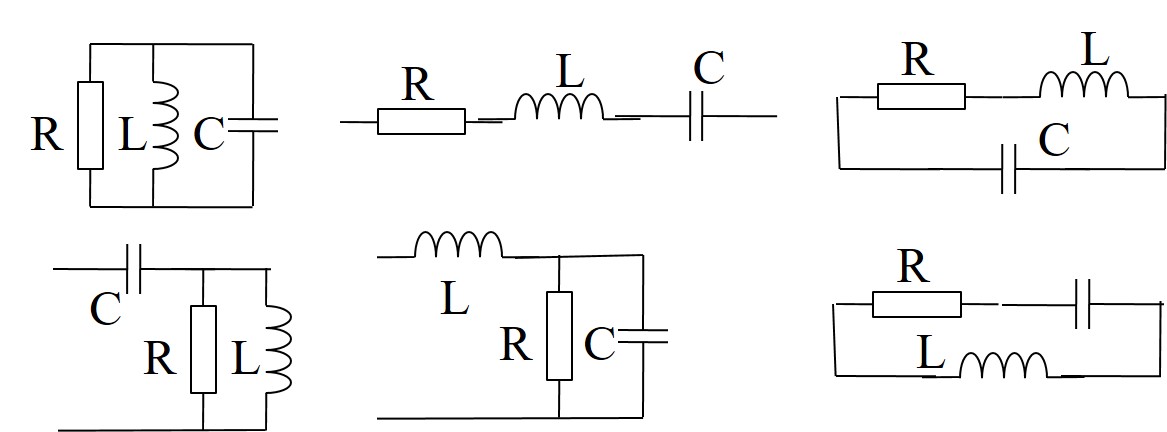
| |
Für die Berechnung der Resonanzfrequenz wird immer der
Imaginärteil des komplexen Widerstandes zu Null gesetzt.
Auch hier kann es zu Spannungs- und Stromüberhöhung kommen.
Auch hier kann es zu Spannungs- und Stromüberhöhung kommen.
Beispiel mehrere Resonanzfrequenzen
|
Berechnen Sie alle Resonanzfrequenzen des Netzes und die Eingangswiderstände bei Resonanz |
\( \underline{Z} = R_1 + \frac{1}{j \omega C_1}
+ \frac{1}{\frac{1}{R_2} + \frac{1}{j \omega L_1} + j \omega C_2} \)
\( \underline{Z} = R_1 + \frac{1}{j \omega C_1} + \frac{1}{\frac{1}{R_2} + j \left( \omega C_2 - \frac{1}{\omega L_1} \right) } \)
\( \underline{Z} = R_1 - j \frac{1}{\omega C_1} + \frac{\frac{1}{R_2} - j \left( \omega C_2 - \frac{1}{\omega L_1} \right) } {\frac{1}{R_2^2} + \left( \omega C_2 - \frac{1}{\omega L_1} \right)^2 } \)
Im{\( \underline{Z} \)} = 0
\( \frac{1}{\omega C_1} = \frac{ \left( \frac{1}{\omega L_1} - \omega C_2 \right) } {\frac{1}{R_2^2} + \left( \omega C_2 - \frac{1}{\omega L_1} \right)^2 } \)
\( \frac{1}{R_2^2} + \left( \omega C_2 - \frac{1}{\omega L_1} \right)^2 = \omega C_1 \left( \frac{1}{\omega L_1} - \omega C_2 \right) \)
\( \frac{1}{R_2^2} + \omega^2 C_2^2 - 2 \frac{C_2}{L_1} + \frac{1}{(\omega L_1)^2} = \frac{C_1}{L_1} - \omega^2 C_1 C_2 \) | · ω2
\( \omega^4 \left( C_2^2 + C_1 C_2 \right) + \omega^2 \left( \frac{1}{R_2^2} - 2 \frac{C_2}{L_1} - \frac{C_1}{L_1} \right) + \frac{1}{(L_1)^2} = 0 \)
Lösung der Gleichung:
\( A x^2 + B x + C = 0 \)
x = ω2
\( A = C_2 \left( C_2 + C_1 \right) = 1.52E-14 s^{4} \)
\( B = \frac{1}{R_2^2} - 2 \frac{C_2}{L_1} - \frac{C_1}{L_1} = 7.58E-6 s^{2} \)
\( C = \frac{1}{(L_1)^2} = 69.4 \)
\( \omega^2 = -\frac{B}{2 A} \pm \sqrt{\frac{B^2}{4 A^2} - \frac{C}{A}} \)
ω1 = 3055 s-1
ω2 = 22108 s-1
Darstellung der komplexen Widerstände
\( \underline{Z} = R_1 + \frac{1}{j \omega C_1} + \frac{1}{\frac{1}{R_2} + j \left( \omega C_2 - \frac{1}{\omega L_1} \right) } \)
\( \underline{Z} = R_1 - j \frac{1}{\omega C_1} + \frac{\frac{1}{R_2} - j \left( \omega C_2 - \frac{1}{\omega L_1} \right) } {\frac{1}{R_2^2} + \left( \omega C_2 - \frac{1}{\omega L_1} \right)^2 } \)
Im{\( \underline{Z} \)} = 0
\( \frac{1}{\omega C_1} = \frac{ \left( \frac{1}{\omega L_1} - \omega C_2 \right) } {\frac{1}{R_2^2} + \left( \omega C_2 - \frac{1}{\omega L_1} \right)^2 } \)
\( \frac{1}{R_2^2} + \left( \omega C_2 - \frac{1}{\omega L_1} \right)^2 = \omega C_1 \left( \frac{1}{\omega L_1} - \omega C_2 \right) \)
\( \frac{1}{R_2^2} + \omega^2 C_2^2 - 2 \frac{C_2}{L_1} + \frac{1}{(\omega L_1)^2} = \frac{C_1}{L_1} - \omega^2 C_1 C_2 \) | · ω2
\( \omega^4 \left( C_2^2 + C_1 C_2 \right) + \omega^2 \left( \frac{1}{R_2^2} - 2 \frac{C_2}{L_1} - \frac{C_1}{L_1} \right) + \frac{1}{(L_1)^2} = 0 \)
Lösung der Gleichung:
\( A x^2 + B x + C = 0 \)
x = ω2
\( A = C_2 \left( C_2 + C_1 \right) = 1.52E-14 s^{4} \)
\( B = \frac{1}{R_2^2} - 2 \frac{C_2}{L_1} - \frac{C_1}{L_1} = 7.58E-6 s^{2} \)
\( C = \frac{1}{(L_1)^2} = 69.4 \)
\( \omega^2 = -\frac{B}{2 A} \pm \sqrt{\frac{B^2}{4 A^2} - \frac{C}{A}} \)
ω1 = 3055 s-1
ω2 = 22108 s-1
Überprüfen mit Excel
MultiResonanz.xlsxDarstellung der komplexen Widerstände
Überprüfen mit LTSPICE
Nachdenken über die Lösung
- Symbolisch rechnen
- Zwischenvariable einführen
- Rechenfehler bemerken
- Zum Schluss ausrechnen
- Gibt es immer eine Resonanz ?
Zusammenfassung und nächstes Mal
- Der Widerstand wird reell ( Im{\( \underline{Z}\)} = 0 = Im{\( \underline{Y}\)}, kein imaginärer Anteil)
- Schaltungsvarianten bei denen Resonanz auftreten kann
- Mehrere Resonanzfrequenzen
- Lösungsüberprüfung
14 Quellen und Leistungsanpassung