Grundlagen Elektrotechnik 2 (GET2)14 LeistungsanpassungProf. Dr. Jörg Vollrath13 Schwingkreis |
|
Video GET2 01 Einführung kompakt
Video der 19. Vorlesung 8.6.2021
|
Länge: 1:22:04 |
0:0:0 Evaluierung 0:0:0 Differenzverstärker 0:2:0 Eingangs und Ausgangswiderstand |
Übersicht
- Quellen und Verbraucher
- Ersatzquellen, Überlagerung, Zusammenfassen
Mehrere Generatoren - Leistung und Verbraucherwiderstand
Lineares aktives Netz
|
  |
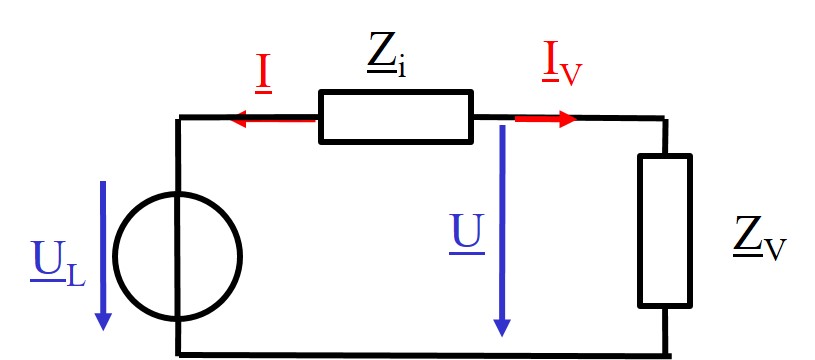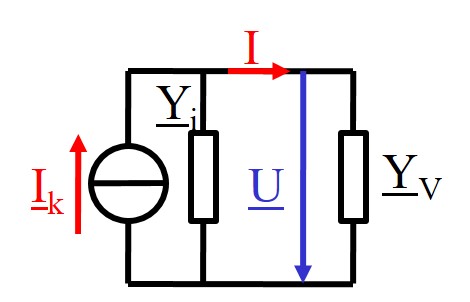Beispiel Ersatzquelle
|
Zwei lineare Sinusquellen
\( \underline{U}_1 = 5 V \underline{/0°} \) mit dem
Innenwiderstand R1 = 100 Ω und C1 = 45 nF und
\( \underline{U}_2 = 8 V \underline{/30°} \) mit dem
Innenwiderstand R2 = 120 Ω und L1 = 2.18 mH
mit der Frequenz f = 10 kHz speisen in Parallelschaltung
einen Grundzweipol R3 = 200 Ω. Wir wollen mit Hilfe von
Ersatzquellen den Strom \( \underline{I}_{R3} \) berechnen. Um die Quellen zusammen zu fassen werden Sie in Stromquellen umgewandelt. Dazu werden die Widerstände in P-Form benötigt. ω = 2 π f = 62800 s^-1 \( \underline{Z}_1 = R_1 + \frac{1}{j \omega C} = 100 \Omega - j \frac{1}{62.8 kHz 45 nF} = 100 \Omega - j 354 \Omega = 367 \Omega \underline{/-74.2°} \) \( \underline{Z}_2 = R_2 + j \omega L = 120 \Omega - j 62.8 kHz 2.18 mH = 120 \Omega + j 137 \Omega = 182 \Omega \underline{/48.8°} \) \( \underline{Y}_1 = 2.72 mS \underline{/74.2°} = 0.741 mS + j 2.62 mS\) \( \underline{Y}_2 = 5.49 mS \underline{/-48.8°} = 3.62 mS - j 4.13 mS\) \( \underline{I}_{K1} = \frac{\underline{U}_1}{R_1 + \frac{1}{j \omega C}} = \underline{U}_1 \underline{Y}_1 = 13.6 mA \underline{/74.2°} = 3.7 mA + j 13.1 mA \) \( \underline{I}_{K2} = \frac{\underline{U}_2}{R_1 + j \omega L} = \underline{U}_2 \underline{Y}_2 = 43.9 mA \underline{/-18.8°} = 41.6 mA - j 14.1 mA \) \( \underline{I} = \underline{I}_{K1} + \underline{I}_{K2} = 45.3 mA - j 1 mA = 45.3 mA \underline{/-1.33°} \) \( \underline{U}_{R3} = \underline{I}_{R3} \cdot R3 = \underline{I} \cdot \underline{Z} \) \( \underline{Z} = \frac{1}{\frac{1}{\underline{Z}_{1}} + \frac{1}{\underline{Z}_{2}} + \frac{1}{R_{3}} } = \frac{1}{\underline{Y}_{1} + \underline{Y}_{2} + G_3 } = \frac{1}{\frac{1}{R_1 + \frac{1}{j \omega C}} + \frac{1}{R_2 + j \omega L} + \frac{1}{R_{3}} } = 105.5 \Omega \underline{/9.2°} \) \( \underline{I}_{R3} = \frac{\underline{I} \cdot \underline{Z}}{R_3} = \frac{\underline{I}_{K1} + \underline{I}_{K2}}{\frac{R_{3}}{R_1 + \frac{1}{j \omega C}} + \frac{R_{3}}{R_2 + j \omega L} + 1 } = \frac{\frac{\underline{U}_1}{R_1 + \frac{1}{j \omega C}} + \frac{\underline{U}_2}{R_2 + j \omega L}} {\frac{R_{3}}{R_1 + \frac{1}{j \omega C}} + \frac{R_{3}}{R_2 + j \omega L} + 1 } = \frac{45.3 mA \underline{/-1.33°} \cdot 105 \Omega \underline{/9.2°}} {200 \Omega} = 23.9 mA \underline{/7.86°} \) \( \underline{I}_{R3} = \frac{\underline{U}_1} {R_{3} + R_{3} \frac{R_1 + \frac{1}{j \omega C}}{R_2 + j \omega L} + R_1 + \frac{1}{j \omega C} } + \frac{\underline{U}_2} {R_{3} \frac{R_2 + j \omega L}{R_1 + \frac{1}{j \omega C}} + R_3 + R_1 + j \omega L } \) Version 4 SHEET 1 880 680 WIRE -848 -896 -1072 -896 WIRE -672 -896 -848 -896 WIRE -560 -896 -672 -896 WIRE -1072 -864 -1072 -896 WIRE -848 -864 -848 -896 WIRE -848 -768 -848 -784 WIRE -560 -768 -560 -896 WIRE -1072 -752 -1072 -784 WIRE -1072 -672 -1072 -688 WIRE -1072 -672 -1120 -672 WIRE -848 -672 -848 -688 WIRE -848 -672 -912 -672 WIRE -1072 -656 -1072 -672 WIRE -848 -656 -848 -672 WIRE -1072 -560 -1072 -576 WIRE -848 -560 -848 -576 WIRE -848 -560 -1072 -560 WIRE -800 -560 -848 -560 WIRE -560 -560 -560 -688 WIRE -560 -560 -800 -560 WIRE -800 -544 -800 -560 WIRE -656 -480 -752 -480 WIRE -256 -480 -656 -480 WIRE -176 -480 -256 -480 WIRE -80 -480 -176 -480 WIRE -656 -464 -656 -480 WIRE -176 -448 -176 -480 WIRE -80 -416 -80 -480 WIRE -752 -400 -752 -480 WIRE -256 -368 -256 -480 WIRE -176 -352 -176 -368 WIRE -656 -336 -656 -384 WIRE -752 -256 -752 -320 WIRE -656 -256 -656 -272 WIRE -656 -256 -752 -256 WIRE -256 -256 -256 -288 WIRE -256 -256 -656 -256 WIRE -176 -256 -176 -272 WIRE -176 -256 -256 -256 WIRE -128 -256 -176 -256 WIRE -80 -256 -80 -336 WIRE -80 -256 -128 -256 WIRE -128 -240 -128 -256 FLAG -800 -544 0 FLAG -672 -896 U FLAG -1120 -672 V1 FLAG -912 -672 V2 FLAG -128 -240 0 FLAG -80 -480 U1 SYMBOL voltage -1072 -672 R0 WINDOW 123 24 124 Left 2 WINDOW 39 0 0 Left 2 SYMATTR Value2 AC 1 SYMATTR InstName V1 SYMATTR Value SINE(0 5 10k) SYMBOL voltage -848 -672 R0 WINDOW 123 24 124 Left 2 WINDOW 39 0 0 Left 2 SYMATTR Value2 AC 1 SYMATTR InstName V2 SYMATTR Value SINE(0 8 10k 0 0 30) SYMBOL cap -1088 -752 R0 SYMATTR InstName C1 SYMATTR Value 45n SYMBOL res -1088 -880 R0 SYMATTR InstName R1 SYMATTR Value 100 SYMBOL res -864 -880 R0 SYMATTR InstName R2 SYMATTR Value 120 SYMBOL ind -864 -784 R0 SYMATTR InstName L1 SYMATTR Value 2.18m SYMBOL res -576 -784 R0 SYMATTR InstName R3 SYMATTR Value 200 SYMBOL cap -672 -336 R0 SYMATTR InstName C2 SYMATTR Value 45n SYMBOL res -672 -480 R0 SYMATTR InstName R4 SYMATTR Value 100 SYMBOL res -192 -464 R0 SYMATTR InstName R5 SYMATTR Value 120 SYMBOL ind -192 -368 R0 SYMATTR InstName L2 SYMATTR Value 2.18m SYMBOL res -96 -432 R0 SYMATTR InstName R6 SYMATTR Value 200 SYMBOL current -256 -288 R180 WINDOW 0 24 80 Left 2 WINDOW 3 24 0 Left 2 WINDOW 123 0 0 Left 2 WINDOW 39 0 0 Left 2 SYMATTR InstName I1 SYMATTR Value SINE(0 43.9m 10k 0 0 -18.8) SYMBOL current -752 -320 R180 WINDOW 0 24 80 Left 2 WINDOW 3 24 0 Left 2 WINDOW 123 0 0 Left 2 WINDOW 39 0 0 Left 2 SYMATTR InstName I2 SYMATTR Value SINE(0 13.6m 10k 0 0 74.2) TEXT -472 -608 Left 2 !.tran 400u |
Version 4 SHEET 1 880 680 WIRE 256 -112 32 -112 WIRE 432 -112 256 -112 WIRE 544 -112 432 -112 WIRE 32 -80 32 -112 WIRE 256 -80 256 -112 WIRE 256 16 256 0 WIRE 544 16 544 -112 WIRE 32 32 32 0 WIRE 32 112 32 96 WIRE 32 112 -16 112 WIRE 256 112 256 96 WIRE 256 112 192 112 WIRE 32 128 32 112 WIRE 256 128 256 112 WIRE 32 224 32 208 WIRE 256 224 256 208 WIRE 256 224 32 224 WIRE 304 224 256 224 WIRE 544 224 544 96 WIRE 544 224 304 224 WIRE 304 240 304 224 FLAG 304 240 0 FLAG 432 -112 U FLAG -16 112 V1 FLAG 192 112 V2 SYMBOL voltage 32 112 R0 WINDOW 123 24 124 Left 2 WINDOW 39 0 0 Left 2 SYMATTR InstName V1 SYMATTR Value SINE(0 5 10k) SYMATTR Value2 AC 1 SYMBOL voltage 256 112 R0 WINDOW 123 24 124 Left 2 WINDOW 39 0 0 Left 2 SYMATTR InstName V2 SYMATTR Value SINE(0 8 10k 0 0 30) SYMATTR Value2 AC 1 SYMBOL cap 16 32 R0 SYMATTR InstName C1 SYMATTR Value 45n SYMBOL res 16 -96 R0 SYMATTR InstName R1 SYMATTR Value 100 SYMBOL res 240 -96 R0 SYMATTR InstName R2 SYMATTR Value 120 SYMBOL ind 240 0 R0 SYMATTR InstName L1 SYMATTR Value 2.18m SYMBOL res 528 0 R0 SYMATTR InstName R3 SYMATTR Value 200 TEXT 144 280 Left 2 !.tran 400u |
Electronic Explorer und R, L, C Bauteil
AWG1 5 V \( \underline{/0°} \) an C, AWG2 8V \( \underline{/30°} \) an L, Rv = 2 * 100 Ω
AWG1 5 V \( \underline{/0°} \) an C, AWG2 8V \( \underline{/30°} \) an L, Rv = 2 * 100 Ω
Messung von Quellenwerten (16.05.2023)
An einem zweipoligen, linearen Netz werden folgende Messungen durchgeführt:| Leerlaufspannung: | U0 = 4.5 V (20 kHz) |
| Kurzschlussstrom: | IK = 50 mA |
| Belastung mit R = 100 Ω : | IR = 24.5 mA |
| Belastung mit C = 0.1 µF: | IC = 52.5 mA |
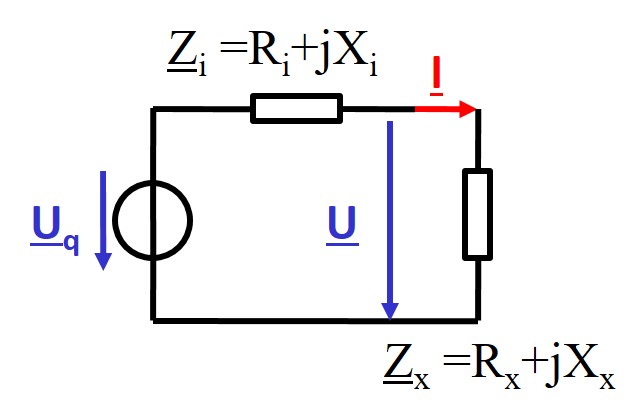
Es können nur Betragswerte gemessen werden und keine Phase.
\( Z_i = \frac{U_q}{I_K} = \frac{4.5 V}{ 50 mA} = 90 \Omega \)
\( Z_i = R_i + j X_i \)
Belastung mit R:
\( I_R = \frac{U_q}{| R + Zi |} = \frac{U_q}{\sqrt{(R+R_i)^2 + X_i^2}}\)
Belastungmit C:
\( I_C = \frac{U_q}{| -\frac{1}{\omega C} + Zi |} = \frac{U_q}{\sqrt{R_i^2 + (-\frac{1}{\omega C} + X_i)^2}}\)
\( (R+R_i)^2 + X_i^2 = \frac{U_q^2}{I_R^2} \)
\( R_i^2 + (-\frac{1}{\omega C} + X_i)^2 = \frac{U_q^2}{I_C^2} \)
\( R^2 + 2 R R_i + R_i^2 + X_i^2 = \frac{U_q^2}{I_R^2} \)
\( R_i^2 + \frac{1}{(\omega C)^2} - \frac{2}{\omega C} X_i + X_i^2 = \frac{U_q^2}{I_C^2} \)
mit \( R_i^2 + X_i^2 = Z_i^2 \)
\( R^2 + 2 R R_i + Z_i^2 = \frac{U_q^2}{I_R^2} \)
\( \frac{1}{(\omega C)^2} - \frac{2}{\omega C} X_i + Z_i^2 = \frac{U_q^2}{I_C^2} \)
\( R_i = \frac{1}{2 R} \left( \frac{U_q^2}{I_R^2} - R^2 - Z_i^2 \right) = 78.2 \Omega\)
\( X_i = \frac{\omega C}{2} \left( \frac{1}{(\omega C)^2} + Z_i^2 - \frac{U_q^2}{I_C^2} \right) = 44.5 \Omega \)
Xi > 0 induktiv
\( L = \frac{X_i}{\omega} = 354 uH \)
Version 4 SHEET 1 880 680 WIRE -240 -768 -384 -768 WIRE -96 -768 -160 -768 WIRE 128 -768 -16 -768 WIRE -384 -720 -384 -768 WIRE -384 -624 -384 -640 WIRE -112 -624 -384 -624 WIRE 128 -624 128 -768 WIRE 128 -624 -112 -624 WIRE -112 -608 -112 -624 WIRE -240 -544 -384 -544 WIRE -96 -544 -160 -544 WIRE 16 -544 -16 -544 WIRE 128 -544 16 -544 WIRE 128 -528 128 -544 WIRE -384 -496 -384 -544 WIRE -384 -400 -384 -416 WIRE -112 -400 -384 -400 WIRE 128 -400 128 -448 WIRE 128 -400 -112 -400 WIRE -112 -384 -112 -400 WIRE -240 -336 -384 -336 WIRE -96 -336 -160 -336 WIRE 16 -336 -16 -336 WIRE 128 -336 16 -336 WIRE 128 -304 128 -336 WIRE -384 -288 -384 -336 WIRE -384 -192 -384 -208 WIRE -112 -192 -384 -192 WIRE 128 -192 128 -240 WIRE 128 -192 -112 -192 WIRE -112 -176 -112 -192 FLAG -112 -176 0 FLAG 16 -336 U2 FLAG -112 -384 0 FLAG 16 -544 U1 FLAG -112 -608 0 SYMBOL voltage -384 -304 R0 WINDOW 123 24 124 Left 2 WINDOW 39 0 0 Left 2 SYMATTR Value2 AC 1 SYMATTR InstName V3 SYMATTR Value SINE(0 4.5 20k) SYMBOL res 0 -320 M270 WINDOW 0 32 56 VTop 2 WINDOW 3 0 56 VBottom 2 SYMATTR InstName R4 SYMATTR Value 78.2 SYMBOL ind -144 -352 R90 WINDOW 0 5 56 VBottom 2 WINDOW 3 32 56 VTop 2 SYMATTR InstName L1 SYMATTR Value 354� SYMBOL voltage -384 -512 R0 WINDOW 123 24 124 Left 2 WINDOW 39 0 0 Left 2 SYMATTR Value2 AC 1 SYMATTR InstName V1 SYMATTR Value SINE(0 4.5 20k) SYMBOL res 0 -528 M270 WINDOW 0 32 56 VTop 2 WINDOW 3 0 56 VBottom 2 SYMATTR InstName R1 SYMATTR Value 78.2 SYMBOL res 112 -544 R0 SYMATTR InstName R2 SYMATTR Value 100 SYMBOL ind -144 -560 R90 WINDOW 0 5 56 VBottom 2 WINDOW 3 32 56 VTop 2 SYMATTR InstName L2 SYMATTR Value 354� SYMBOL voltage -384 -736 R0 WINDOW 123 24 124 Left 2 WINDOW 39 0 0 Left 2 SYMATTR Value2 AC 1 SYMATTR InstName V2 SYMATTR Value SINE(0 4.5 20k) SYMBOL res 0 -752 M270 WINDOW 0 32 56 VTop 2 WINDOW 3 0 56 VBottom 2 SYMATTR InstName R3 SYMATTR Value 78.2 SYMBOL ind -144 -784 R90 WINDOW 0 5 56 VBottom 2 WINDOW 3 32 56 VTop 2 SYMATTR InstName L3 SYMATTR Value 354� SYMBOL cap 112 -304 R0 SYMATTR InstName C2 SYMATTR Value 0.1� TEXT -408 -128 Left 2 !.tran 400u TEXT 184 -696 Left 2 !.meas imax max i(R3)\n.meas imin min i(R3)\n.meas imaxR max i(R1)\n.meas iminR min i(R1)\n.meas imaxC max i(R4)\n.meas iminC min i(R4)\n.meas ik param (imax-imin)/2\n.meas iR param (imaxR-iminR)/2\n.meas iC param (imaxC-iminC)/2
Leistungsanpassung
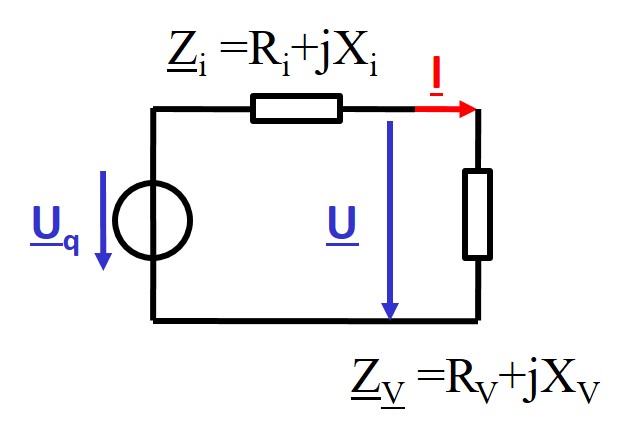
Eine Quelle gibt die maximal mögliche Leistung an einen Verbraucher.
Lineares Gleichstromnetz: Ri = Rv
Lineares Netz an Sinusspannungen:
Verbraucherwirkleistung P:
\( P = R_V I^2 = R_v \frac{U_q^2}{(R_i + R_v)^2 + (X_i + X_v)^2} \)
Wahl von Rv und Xv für Maximum
Leistungsanpassung Herleitung
\( P = R_V I^2 = R_v \frac{U_q^2}{(R_i + R_v)^2 + (X_i + X_v)^2} \)
Wahl von Rv und Xv für Maximum
(1) Xv = - Xi
(2) Rv = Ri
Das Maximum der Wirkleistung tritt bei Resonanz auf.
Herleitung Rv für Maximum: \( \frac{d P}{d R_v} = 0 \)
\( P_{opt} = R_v \frac{U_q^2}{(R_i + R_v)^2} \)
\( \frac{d P_{opt}}{d R_v} = U_q^2 \left( \frac{1}{(R_i + R_v)^2} + \frac{-2 \cdot R_v}{(R_i + R_v)^3} \right) = 0 \)
\( \frac{d P_{opt}}{d R_v} = U_q^2 \frac{R_i + R_v -2 \cdot R_v}{(R_i + R_v)^3} = 0 \)
\( R_i + R_v -2 \cdot R_v = 0 \)
\( R_i - R_v = 0 \)
\( R_i = R_v \)
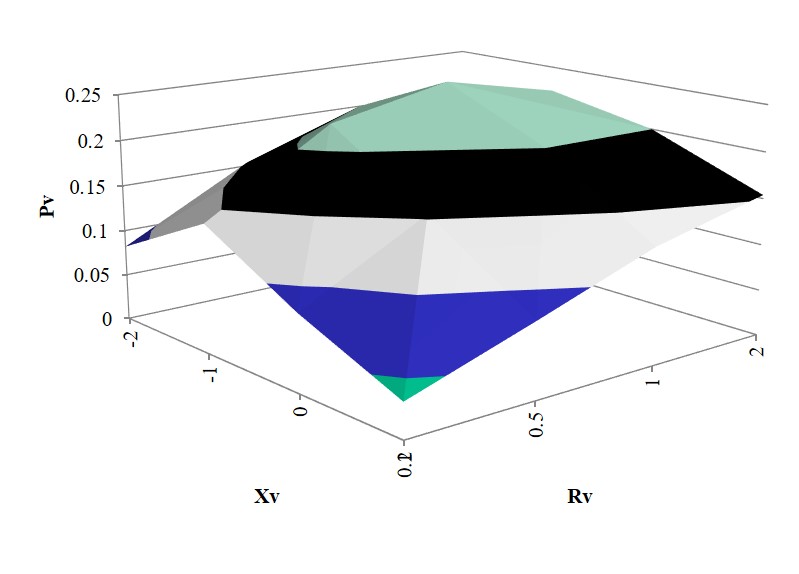
Maximale Wirkleistung
\( P_{max} = \frac{U_q^2}{ 4 R_i } = \frac{I_q^2}{ 4 G_i } \)
Wirkleistungsanpassung ist frequenzabhängig
Nachrichtentechnik: Leistungsanpassung in einem großen Frequenzbereich. Scheinleistungsanpassung
\( \underline{Z}_v = \underline{Z}_i \)
Scheinleistung SSA am Verbraucher
\( S_{SA} = \frac{U_q^2}{ 4 Z_i } = \frac{I_q^2}{ 4 Y_i } \)
\( P_{SA} = \frac{R_i}{Z_i} S_{SA} = \frac{U_q^2}{ 4 Z_i^2 } R_i = \frac{U_q^2}{ 4 R_i ( 1 + \frac{X_i^2}{R_i^2})} \)
Bei kleinen Winkeln des komplexen Widerstandes ist PSA nur unwesentlich kleiner als die maximale Wirkleistung Pmax bei Wirkleistungsanpassung.
Beispiel Scheinleistungsanpassung
An einer Quelle mit der Quellenspannung Uq = 1.5 V und dem komplexen Innenwiderstand Zi = (1 - j 0.25) MΩ wird ein Verbraucher bei Scheinleistungsanpassung betrieben. Wir wollen untersuchen, um wie viel Prozent seine Wirkleistung PSA kleiner ist als die maximale Wirkleistung Pmax bei Wirkleistungsanpassung.
Scheinleistungsanpassung: \( \underline{Z}_V = \underline{Z}_i \)
\( I = \frac{U_q}{2 Z_i} = \frac{U_q}{2 \sqrt{R_i^2 + X_i^2}} \)
Wirkleistung des Verbrauchers:
\( P_{SA} = R_V I^2 = \frac{R_V U_q^2}{4 ( R_i^2 + X_i^2)} = 0.53 \mu W \)
\( P_{max} = \frac{U_q^2}{4 R_i} = 0.56 \mu W \)
\( \frac{\Delta P}{P_{max}} = \frac{P_{max} - P_{SA}}{P_{max}} = \frac{0.03}{0.56} = 6 \% \)
\( I = \frac{U_q}{2 Z_i} = \frac{U_q}{2 \sqrt{R_i^2 + X_i^2}} \)
Wirkleistung des Verbrauchers:
\( P_{SA} = R_V I^2 = \frac{R_V U_q^2}{4 ( R_i^2 + X_i^2)} = 0.53 \mu W \)
\( P_{max} = \frac{U_q^2}{4 R_i} = 0.56 \mu W \)
\( \frac{\Delta P}{P_{max}} = \frac{P_{max} - P_{SA}}{P_{max}} = \frac{0.03}{0.56} = 6 \% \)
Leistungsanpassung in der Nachrichtentechnik
Bei einer elektrischen Übertragung müssen bei langen Leitungen (ab einer Länge von etwa 10% der Wellenlänge des Signales) die Impedanzen leistungsangepasst werden (Widerstandsanpassung), um Reflexionen des Signals an den Verbindungen der Leitung zu verhindern, die störende Rückwirkungen verursachen. (Matching)
Zv=Zi
In breitbandigen Kabeldatennetzen und Kabelverbindungen für steile Impulse treten bei Fehlanpassung Reflexionen und verformte Flanken auf, was zu Fehlern führt (siehe Zeitbereichsreflektometrie). Daher muss darauf geachtet werden, dass alle Komponenten die Kabel mit der korrekten Impedanz abschließen:
50…75 Ω bei Koaxialkabeln,
100…150 Ω bei Zweidrahtleitungen (twisted pair)
600 Ω bei der analogen Telefontechnik
Leistungsanpassung in der Energietechnik
Bei großen Leistungen, wie sie in der Energie- und Kraftwerkstechnik auftreten, würde bei Leistungsanpassung die Quelle unzulässig erwärmt werden, da wegen RL = RI die gleichen Leistungen in RL und RI umgesetzt werden. Außerdem wären der niedrige Wirkungsgrad und der hohe Spannungsabfall ungünstig und nicht im Sinne der Energieversorgungsunternehmen. In der Energietechnik sind daher die Betriebsströme kleiner als 10 % des Kurzschlussstroms.
Blindleistungskompensation
- Zusätzliche Verluste in der elektrischen Energieversorgung
Energie fließt zwischen Verbraucher und Erzeuger infolge der Blindleistung - Zuschalten eines Zweipols am Verbrauchers:
\( \underline{Y}_V = G_V + j B_V \)
Parallelschaltung – BV
Blindleistungskompensation
Induktiven Verbrauchern (Motoren) werden Kondensatoren parallel geschaltet.
Parallelkompensation, da sich durch Reihenschaltung die Spannung am Verbraucher ändern würde.
Blindleistungskompensation
|
Version 4 SHEET 1 880 680 WIRE 240 96 96 96 WIRE 480 96 240 96 WIRE 576 96 480 96 WIRE 480 128 480 96 WIRE 576 160 576 96 WIRE 240 176 240 96 WIRE 240 272 240 240 WIRE 240 272 96 272 WIRE 480 272 480 208 WIRE 480 272 240 272 WIRE 576 272 576 240 WIRE 576 272 480 272 SYMBOL cap 256 240 R180 WINDOW 0 24 56 Left 2 WINDOW 3 24 8 Left 2 SYMATTR InstName C1 SYMATTR Value 3n SYMBOL res 592 256 R180 WINDOW 0 36 76 Left 2 WINDOW 3 36 40 Left 2 SYMATTR InstName R1 SYMATTR Value 1k SYMBOL ind 496 224 R180 WINDOW 0 36 80 Left 2 WINDOW 3 36 40 Left 2 SYMATTR InstName L1 SYMATTR Value 4m TEXT 160 -32 Left 2 !VDD N001 N004 SINE(0 1 10k) TEXT 160 -8 Left 2 !.tran 1m TEXT 264 -8 Left 2 !R N004 0 0.1 TEXT 320 184 Left 2 ;PV LINE Normal 368 80 368 48 2 LINE Normal 368 256 368 112 2 LINE Normal 368 320 368 288 2 LINE Normal 624 48 368 48 2 LINE Normal 624 320 624 48 2 LINE Normal 368 320 624 320 2 |
Zusammenfassung und nächstes Mal
- Leistungsanpassung
- Wirkleistungsanpassung, Scheinleistungsanpassung, Blindleistungskompensation, MPP
Hochschule für angewandte Wissenschaften Kempten, Jörg Vollrath, Bahnhofstraße 61 · 87435 Kempten
Tel. 0831/25 23-0 · Fax 0831/25 23-104 · E-Mail: joerg.vollrath(a)hs-kempten.de
Impressum