Grundlagen Elektrotechnik 2 (GET2)15 NetzfunktionenProf. Dr. Jörg Vollrath14 Leistungsanpassung |
|
Video GET2 01 Einführung kompakt
Video der 19. Vorlesung 8.6.2021
|
Länge: 1:22:04 |
0:0:0 Evaluierung 0:0:0 Differenzverstärker 0:2:0 Eingangs und Ausgangswiderstand |
Rückblick und Heute
- Leistungsanpassung
- Wirkleistungsanpassung, Scheinleistungsanpassung
- Blindleistungskompensation
Heute:
- Netzfunktion
- Grenzfälle \( \omega = 0 \) und \( \omega = \infty \)
- Komponentendarstellung
- Normierung mit einem Bezugswiderstand und einer Bezugsfrequenz
- Impedanz
Netzfunktion
Es wird ein Netz bei verschiedenen Frequenzen \( \omega \) untersucht.- Idealer kapazitiver Zweipol
\( I = \omega C U \), \( \phi_C = -90° \), \( \underline{Y}\left( j \omega \right) = j \omega C \) - Idealer induktiver Zweipol
\( U = \omega L I \), \( \phi_L = 90° \), \( \underline{Z}\left( j \omega \right) = j \omega L \)
Netzfunktion
\( \underline{F}\left( j \omega \right) = Re \left\{ \underline{F}\left( j \omega \right) \right\} + j Im \left\{ \underline{F}\left( j \omega \right) \right\} \)
Nach Potenzen von \( j \omega \) kann man gerade und ungerade Funktionen unterscheiden:
Gerade Funktion: Realteil, Betrag \( \left( j \omega \right)^{0}, \left( j \omega \right)^{2}, \left( j \omega \right)^{-2}, ... \)
Ungerade Funktion: Imaginärteil, Phase \( \left( j \omega \right)^{1}, \left( j \omega \right)^{-1}, \left( j \omega \right)^{3}, ... \)
Widerstandsfunktion eines Netzes
|
Gesucht ist die Widerstandsfunktion folgenden Netzes:
\( \underline{Z} \left( j \omega \right) = j \omega L_1
+ \frac{1}{G_2 + j \omega C_1} \)
Zerlegung in Realteil und Imaginärteil durch konjugiert komplexe Erweiterung. \( \underline{Z} \left( j \omega \right) = j \omega L_1 + \frac{1}{G_2 + j \omega C_1} \frac{G_2 - j \omega C_1}{G_2 - j \omega C_1} \) \( \underline{Z} \left( j \omega \right) = j \omega L_1 + \frac{G_2 - j \omega C_1}{G_2^2 + \left( \omega C_1 \right)^2} \) \( \underline{Z} \left( j \omega \right) = \frac{G_2}{G_2^2 + \left( \omega C_1 \right)^2} + j \omega \left( L_1 - \frac{C_1}{G_2^2 + \left( \omega C_1 \right)^2} \right) \) |
Zur Erstellung der Widerstandsfunktion geht man ausgehend von einer Klemme entlang den Verbindungen
eines Netzwerkes bis zur zweiten Klemme.
Serienwiderstände werden addiert. Trifft man auf eine Verzweigung und liegt
keine Dreieckschaltung vor, erstellt man den Widerstand der Parallelschaltung
durch den Reziprokwert der Summe der Leitwerte.
Untersuchung bei verschiedenen Kreisfrequenzen:
Grenzfälle
Untersuchung für \( \omega = 0 \)
- Idealer induktiver Zweipol:
Kurzschluss - Idealer kapazitiver Zweipol:
Unterbrechung
- Idealer induktiver Zweipol:
Unterbrechung - Idealer kapazitiver Zweipol:
Kurzschluss
Videolösung
Normierung
Erzeugen einer dimensionslosen Größe:
Es wird mit einem Bezugswiderstand oder Bezugsleitwert normiert.
Die Netzfunktion wird klein geschrieben:
\( \underline{z}\left( j \omega \right) = \frac{\underline{Z}\left( j \omega \right)}{R_{Bez}}\)
Normierung der Kreisfrequenz:
\( \Omega = \frac{\omega }{\omega_{Bez}} = \frac{f}{f_{Bez}} \)
Bei RBez = 1 Ω und ω = 1 s-1 sieht es so aus, als ob man die Einheit wegläßt.
Beispiel
Für das gezeigte Netz sind die Werte \( R_1 = 1 k\Omega ; L_1 = 120 mH; G_2 = 0,8 mS \) und \( C_1 = 0,18 \mu F \) gegeben. Wir wollen die Widerstandsfunktion des Netzes mit dem Bezugswiderstand \( R_{Bez} = R_1 = 1 k\Omega \) normieren und den normierten Wirkwiderstand \( r(\Omega) \) sowie den normierten Blindwiderstand \( x(\Omega) \) über der normierten Frequenz darstellen.
\( \underline{Z} \left( j \omega \right) =
R_1 + \frac{G_2}{G_2^2 + \left( \omega C_1 \right)^2}
+ j \omega \left( L_1 -
\frac{C_1}{G_2^2 + \left( \omega C_1 \right)^2} \right) \)
\( \Omega = \frac{\omega}{\omega_{bez}} \)
\( \underline{r} \left( \omega \right) = \frac{R_1}{R_{bez}} + \frac{1}{R_{bez} G_2 + \frac{R_{bez}}{G_2} \omega^2 C_1^2} \)
Zur Normierungsfrequenz bietet es sich an den Term:
\( \frac{R_{bez}}{G_2} \omega^2 C_1^2 \)
mit Ω2 zu ersetzen.
Dann wäre
\( \frac{R_{bez}}{G_2} \omega^2 C_1^2 = \Omega^2 \)
\( \frac{\omega^2}{\frac{G_2}{R_{bez} C_1^2} } = \Omega^2 \)
\( \omega_{bez} = \sqrt{\frac{G_2}{R_{bez} C_1^2}} = 4969 s^{-1} \)
Dann ist die normierte Wirkwiderstandsfunktion:
\( \underline{r} \left( \omega \right) = 1 + \frac{1}{0.8 + \Omega^2 } \)
Excel: Widerstandsfunktion.xlsx
LTSPICE: U/I
\( \Omega = \frac{\omega}{\omega_{bez}} \)
\( \underline{r} \left( \omega \right) = \frac{R_1}{R_{bez}} + \frac{1}{R_{bez} G_2 + \frac{R_{bez}}{G_2} \omega^2 C_1^2} \)
Zur Normierungsfrequenz bietet es sich an den Term:
\( \frac{R_{bez}}{G_2} \omega^2 C_1^2 \)
mit Ω2 zu ersetzen.
Dann wäre
\( \frac{R_{bez}}{G_2} \omega^2 C_1^2 = \Omega^2 \)
\( \frac{\omega^2}{\frac{G_2}{R_{bez} C_1^2} } = \Omega^2 \)
\( \omega_{bez} = \sqrt{\frac{G_2}{R_{bez} C_1^2}} = 4969 s^{-1} \)
Dann ist die normierte Wirkwiderstandsfunktion:
\( \underline{r} \left( \omega \right) = 1 + \frac{1}{0.8 + \Omega^2 } \)
Excel: Widerstandsfunktion.xlsx
LTSPICE: U/I
Lautsprecherimpedanz
Wikipedia:
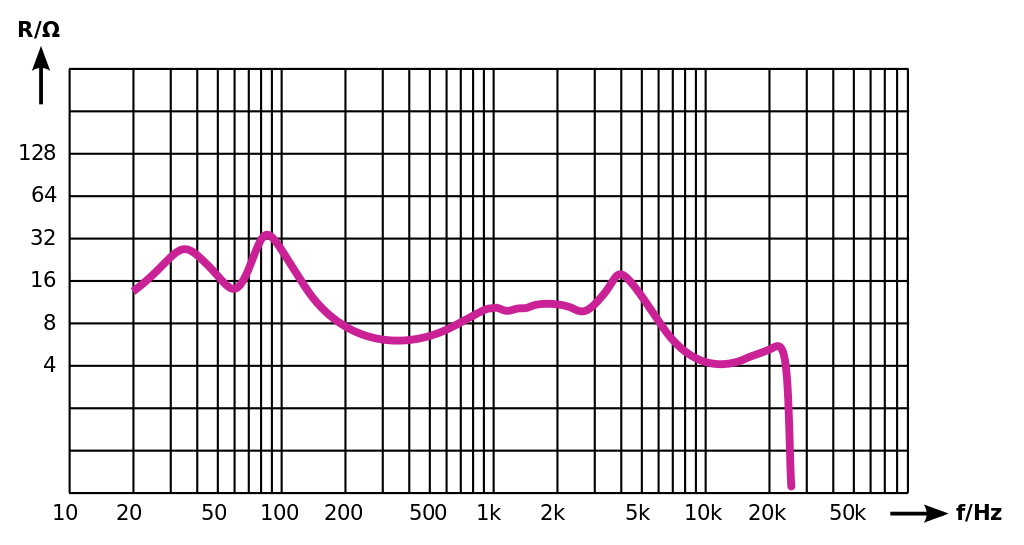
Elektrodynamische Lautsprecher werden mit Wechselstrom betrieben.
Deshalb verursacht der induktive Widerstand der eingebauten Schwingspule
eine Phasenverschiebung zwischen Strom und Spannung, die frequenzabhängig ist.
Aus diesem Grund wird nicht vom Widerstand gesprochen,
sondern von der Impedanz des Lautsprechers.
DIN Norm
Bei Lautsprecherboxen wird nach DIN EN 60268-5 eine Angabe der Impedanz gefordert. Die Impedanz ist jedoch von der Frequenz abhängig.
Der angegebene Impedanzwert (z. B. 4 Ω) darf nur um 20 % unterschritten werden.
DIN Norm
Bei Lautsprecherboxen wird nach DIN EN 60268-5 eine Angabe der Impedanz gefordert. Die Impedanz ist jedoch von der Frequenz abhängig.
Der angegebene Impedanzwert (z. B. 4 Ω) darf nur um 20 % unterschritten werden.