Grundlagen Elektrotechnik 2 (GET2)16 OrtskurvenProf. Dr. Jörg Vollrath15 Netzfunktionen |

|
Video GET2 01 Einführung kompakt
Video der 19. Vorlesung 8.6.2021
|
Länge: 1:22:04 |
0:0:0 Evaluierung 0:0:0 Differenzverstärker 0:2:0 Eingangs und Ausgangswiderstand |
Rückblick und Heute
- Netzfunktion
- Grenzfälle \( \omega = 0 \) und \( \omega \rightarrow \infty \)
- Komponentendarstellung
- Normierung mit einem Bezugswiderstand und einer Bezugsfrequenz
- Ortskurvendarstellung
Heute:
- Ortskurven (Nyquist Plot)
Ortskurvendarstellung
- Grafische Veranschaulichung einer Netzfunktion
- Rechtwinkliges Koordinatensystem
- Realteil auf der Abszisse
- Imaginärteil auf der Ordinate
- Variable:
- Frequenz
- Veränderlicher Widerstand
- Untersuchung für den Parameter Kreisfrequenz ?
- ω = 0 bis \( \omega \rightarrow \infty \)
- Wie sehen die Ortskurven einzelner Bauelemente R, L, C aus?
- Was passiert mit Ortskurven bei Reihen- und Parallelschaltung?
Widerstandsfunktion eines Netzes
|
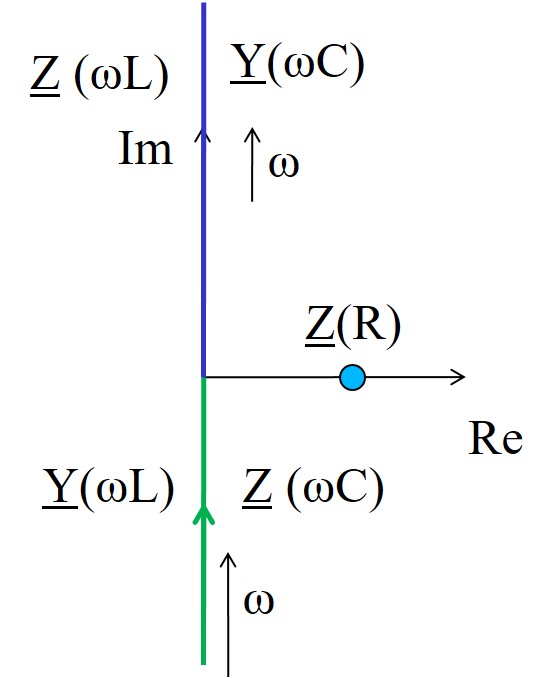
\( \underline{Z}(\omega L) = j \omega L \) \( \underline{Y}(\omega L) = -j \frac{1}{\omega L} \) \( \underline{Z}(\omega C) = -j \frac{1}{\omega C} \) \( \underline{Y}(\omega C) = j \omega C \)
|
|
Eine Ortskurve trägt man in einem komplexen Koordinatensystem mit
x-Achse Realteil und y-Achse Imaginärteil auf.
Für verschiedene Frequenzen ensteht eine Kurve, bei der mit einem Pfeil die Richtung des Verlaufs für größere Frequenzen angegeben wird.
Ein ohmscher Widerstand ist nur ein Punkt auf der Reellen Achse.
Eine Kapazität und eine Induktivität sind jeweils Halbgeraden auf der imaginären Achse.
Für verschiedene Frequenzen ensteht eine Kurve, bei der mit einem Pfeil die Richtung des Verlaufs für größere Frequenzen angegeben wird.
Ein ohmscher Widerstand ist nur ein Punkt auf der Reellen Achse.
Eine Kapazität und eine Induktivität sind jeweils Halbgeraden auf der imaginären Achse.
Ortskurve und Reihenschaltung
|
Ortskurven Eigenschaften
- Beliebige Netzfunktionen
- Ortskurven nur in der rechten Halbebene
- Imaginärteil bleibt entweder positiv oder negativ wenn gleichartige Energiespeicher im Netz sind.
- Ortskurve verläuft dann entweder in der oberen oder unteren Halbebene
- Bei verschiedenartigen Energiespeichern kann die Kurve oberhalb und unterhalb verlaufen
- Bei Nulldurchgang befindet sich dann die Resonanzfrequenz
- Normierung ist sehr wichtig bei der Darstellung verschiedener Netzfunktionen
Ortskurven zueinander inverser Funktionen
- Übergang Widerstandsfunktion zur Leitwertfunktion
- \( \underline{Y}(j \omega ) = \frac{1}{\underline{Z}(j\omega )} \)
- Inversion, inverse Funktion
- Abbildung der Funktion
- Beide Kurven in der selben Abbildung: Normierung Rbez
- \( \underline{z}(j\omega) = \frac{\underline{Z}(j\omega )}{R_{bez}} \)
- \( \underline{y}(j\omega) = \frac{1}{\underline{z}(j\omega)} = R_{bez} \underline{Y}(j\omega) \)
- Einfache Inversion in der P-Form
- \( \underline{Z} = Z \underline{/\phi} = \frac{1}{Y} \underline{/-\phi} \)
- Durch die Inversion werden Punkte der oberen Halbebene in die untere Halbebene abgebildet und umgekehrt
- Ursprungsnächster wird ursprungsfernster Punkt
- Ursprungsfernster wird ursprungsnächster Punkt
Ortskurve Test (13.5.2025)
Rbez = 0.8 R
Ortskurve Test
Rbez = 0.8 R
Spezielle Ortskurve
|
Rbez = 0.8 R Ortskurve Leitwert
|
Was wird auf der Folie dargestellt?
Wie kommt man zur Ortskurvendarstellung des Leitwertes?
Welche Regeln gibt es?
Excel Ortskurve
Wie kommt man zur Ortskurvendarstellung des Leitwertes?
Welche Regeln gibt es?
Excel Ortskurve
Regeln zur Entwicklung von Ortskurven
- Normierung
- Schrittweises Zusammenfassen der Elemente
- Inversion (Leitwert ↔ Widerstand)
- Positive ↔ Negative Halbebene
- Vorzeichen des Winkels ändert sich.
- Ursprungsnaher Punkt ↔ Ursprungsferner Punkt
- Punktweise Addition
- Überprüfen mit Excel
Praktische Bedeutung:
- Aus der Ortskurve kann man die Elemente eines Netzwerkes bestimmen.
- Modellierung und Analyse unbekannter Netze
Beispiel Ortskurve
|
Rbez = 0.9 R1 |
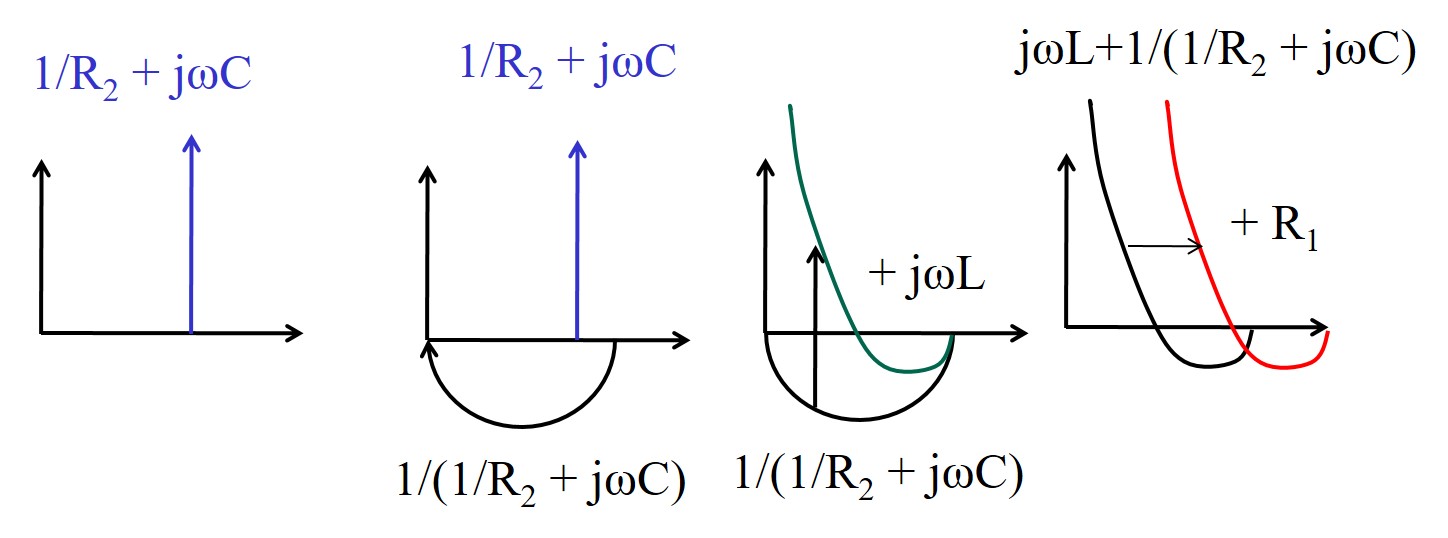
Wo ist die 1 auf der reellen Achse?
Beispiel Ortskurve
|
Wir wollen die Y-Ortskurve der Schaltung bestimmen. |
Beispiel Ortskurve LTSPICE
|
Es ist folgende Schaltung mit \( R_1 = 1 k\Omega,
C_1 = 18 nF, R_2 = 3 k\Omega, L_1 = 32 mH \) gegeben. 2.1. Berechnen Sie den komplexen Eingangswiderstand in R-Form und P-Form für \( f = 125 kHz\). 2.2. Berechnen Sie die Resonanzfrequenz. 2.3. Für welche Widerstandswerte \( R_2 \) gibt es keine Resonanz? |
Lösung:
\( \underline{Z} = \frac{1}{\frac{1}{R_2} + \frac{1}{R_1 + j \omega L_1}} + \frac{1}{j \omega C_1} \)
Bei der Umformung eliminiert man Brüche und bringt Unterbrüche auf einen gemeinsamen Nenner bis man nur noch einen Bruch hat.
Dann kann man konjugiert komplex erweitern.
\( \underline{Z} = \frac{R_2 \left(j \omega L_1 + R_1 \right)} {j \omega L_1 + R_1 + R_2} + \frac{1}{j \omega C_1} \)
Ersten Teil konjugiert komplex erweitern:
\( \underline{Z} = \frac{R_2 \left(j \omega L_1 + R_1 \right) \left( R_1 + R_2 - j \omega L_1 \right)} {\left(\omega L_1 \right)^2 + \left(R_1 + R_2\right)^2} + \frac{1}{j \omega C_1} \)
\( \underline{Z} = R_2 \frac{j \omega L_1 \left( R_1 + R_2 - R_1 \right) + R_1 \left( R_1 + R_2 \right) + \omega^2 L_1^2} {\left(\omega L_1 \right)^2 + \left(R_1 + R_2\right)^2} + \frac{1}{j \omega C_1} \)
\( \underline{Z} = R_2 \frac{ R_1 \left( R_1 + R_2 \right) + \omega^2 L_1^2} {\left(\omega L_1 \right)^2 + \left(R_1 + R_2\right)^2} + j \left( \frac{\omega L_1 R_2^2 } {\left(\omega L_1 \right)^2 + \left(R_1 + R_2\right)^2} - \frac{1}{\omega C_1} \right) \)
\( \underline{Z} = 2.94 k\Omega + j 279 \Omega = 2957 \Omega \underline{/5.4°} \)
Imaginärteil von \( \underline{Z} \) gleich 0 setzen
\( Im\{\underline{Z}\} = \frac{ \omega L_1 R_2^2} {\left(\omega L_1 \right)^2 + \left(R_1 + R_2\right)^2} - \frac{1}{\omega C_1} = 0 \)
\( \omega^2 C_1 L_1 R_2^2 = \left(\omega L_1 \right)^2 + \left(R_1 + R_2\right)^2 \)
\( \omega^2 \left(C_1 L_1 R_2^2 - L_1^2 \right) = \left(R_1 + R_2\right)^2 \)
\( \omega^2 = \frac{\left(R_1 + R_2\right)^2} {C_1 L_1 R_2^2 - L_1^2} \)
\( \omega = \sqrt{\frac{\left(R_1 + R_2\right)^2} {C_1 L_1 R_2^2 - L_1^2}} = s^{-1} \)
\( C_1 L_1 R_2^2 - L_1^2 \lt 0 \)
\( R_2 \lt \sqrt{\frac{L_1}{C_1}} = 1.33 k\Omega \)
Verifikation des Ergebnisses mit LTSPICE
In LTSPICE verifiziert man diese Lösung mit einer Stromquelle am Eingang mit 1 A.
Mit der AC Simulation wird dann \( \underline{Z} = \frac{\underline{U_1}}{\underline{I}} \) dargestellt.
Für die Frequenz 125 kHz liest man bei linearer Skalierung die P-Form ab: 3 kOhm und 5° ab.
Mit linker Maustaste (LMT) kann man für die y-Achse 'Nyquist' wählen und die Ortskurve darstellen.
Dann bekommt man die R-Form: R = 2.94 kΩ und X = 294 Ω.
Schaltungen Ortskurve
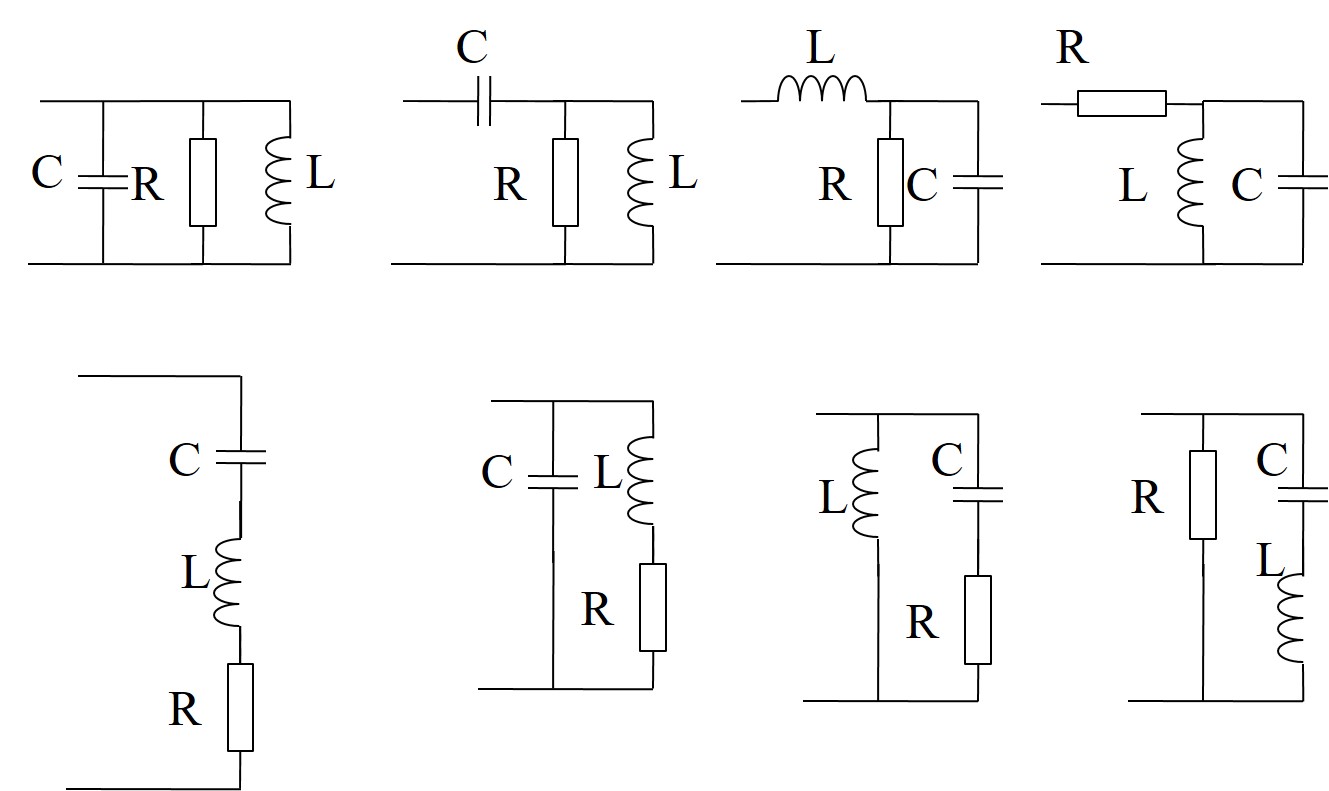
Li-Ion Akkumessung mit Ortskurven
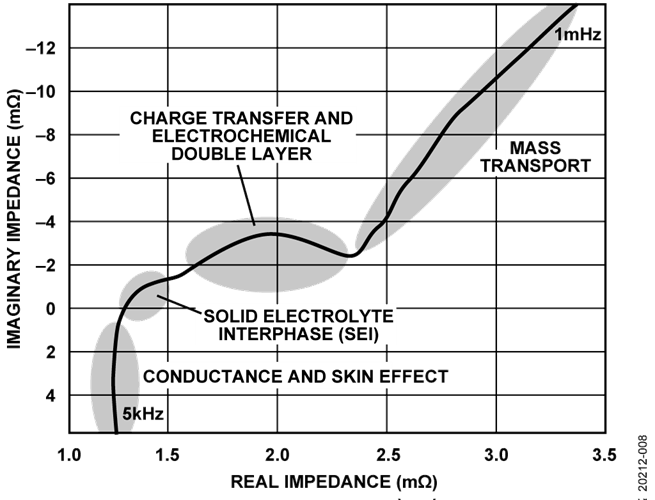 Figure 2. Nyquist Plot for a Battery Showing the Different Regions Corresponding to an Electrochemical Process Electrochemical Impedance Spectroscopy (EIS) for Batteries, Analog Devices |
Der Schaltplan BatteryESBimpedance.asc enthält die schrittweise Entwicklung
des Ersatzschaltbildes.
Zusammenfassung und nächstes Mal
- Komplexes Koordinatensystem
- Ortskurven von R, L und C
- Inversion zwischen Widerstand und Leitwert
- Beispiele