Grundlagen Elektrotechnik 2 (GET2)18 Bode DiagramProf. Dr. Jörg Vollrath17 Übertragungsfunktion |

|
Video GET2 01 Einführung kompakt
Video der 19. Vorlesung 8.6.2021
|
Länge: 1:22:04 |
0:0:0 Evaluierung 0:0:0 Differenzverstärker 0:2:0 Eingangs und Ausgangswiderstand |
Übersicht
- Frequenzgang
- Maß, Betrag, Phase
- Amplitudengang, Phasengang, Pole, Nullstellen
Ziele Frequenzgang
- die Begriffe Frequenzgang, Amplitudengang und Phasengang an Beispielen erläutern.
- ein Beispiel für ein Übertragungssystem nennen.
- für ein Übertragungssystem einen Übertragungsfaktor definieren.
- für ein einfaches elektrisches Netz die Übertragungsfunktion berechnen.
- die Bezeichnung Dezibel erläutern
- den Frequenzgang einer Größe mit dem BODE-Diagramm darstellen.
Frequenzgang Inhalt
- Übertragungsfaktor und Dämpfungsfaktor
- Spannungsübertragungsfaktor
- Stromübertragungsfaktor
- Betriebsübertragungsfaktor
- Betriebsdämpfungsfaktor
- Logarithmierte Größenverhältnisse
- Dezibel und Neper
- Pol Nullstellen Plan
- Bode Diagramm
Frequenzgangsfunktionen und Übertragungssystem
- Frequenzgangsfunktionen
- Nachrichtenübertragungssysteme (transmission systems)
- Signale (signal)
- Beispiel: Strom einer Spule, Spannung eines Kondensatormikrofons
- Komponenten eines Übertragungssystem
- Sender (transmitter)
- Übertragungskanal (transmission channel)
- Empfänger (receiver)
- Nachrichtenquelle
- Leitung
- Nachrichtensenke
- Signale: Spannungen, Ströme
Übertragungsfaktor und Dämpfungsfaktor
- Übertragungsfaktor (transfer function)
- Quotient aus Ausgangs- und Eingangsgröße
- Übertragungsfaktor
- \( \underline{T}_{21} (j \omega ) = \frac{\underline{U}_{2} (j \omega ) }{\underline{U}_{1} (j \omega )} \)
- \( \underline{T}_{V1} (j \omega ) = \frac{\underline{I}_{V} (j \omega ) }{\underline{U}_{1} (j \omega )} \)
- Dämpfungsfaktor (attenuation function)
- \( \underline{D}_{qV} (j \omega ) = \frac{\underline{U}_{q} (j \omega ) }{\underline{U}_{V} (j \omega )} \)
- Dämpfungsfunktion
Amplitudengang und Phasengang
- Definition: Frequenzgang:
- Eine Netzfunktion der Abhängigkeit einer Sinusfunktion oder eines Quotienten von der Frequenz
- Gleichung, Kurve, Tabelle
- Amplitudengang
- Phasengang
- Normierung: Bezug auf Quellengrößen
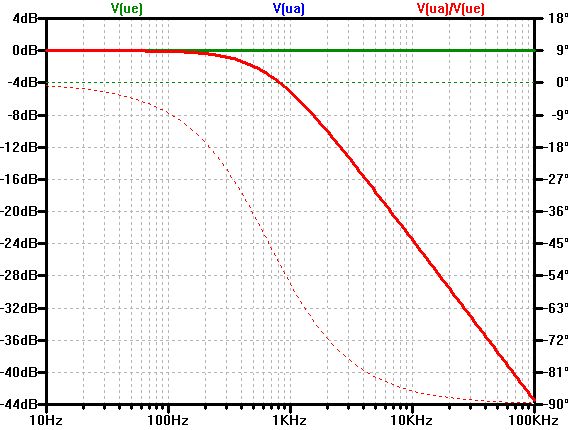
Bode Diagram, Pole und Nullstellen
|
\( \frac{\underline{U}_{A}}{\underline{U}_E} = \frac{R_1}{L_1} \frac{1}{j \omega + \frac{R_1}{L_1} } \) |
| |
|
\( \underline{T} (j\omega) = K \frac{(j \omega - s_{N1})(j \omega - s_{N2})...(j \omega - s_{Nm})}
{(j \omega - s_{P1})(j \omega - s_{P2})...(j \omega - s_{Pn}) } \) | ||
- Eine Übertragungsfunktion kann in einen Übertragungsfaktor \( \underline{T} (j \omega) \) mit Polen sPi und Nullstellen sNi überführt werden.
- Diese Darstellung erlaubt es ein Bode Diagramm zu erstellen.
- Frequenzgang: x-Achse: log(f) y-Achse: \( log( |\underline{t}(j \omega ) |) \) Maß
- Phasengang: x-Achse: log(f) y-Achse: φ
Übertragungsfunktion und Maß
Übertragungsfunktion (Transfer function)
\( \underline{T} (j\omega) = \frac{\underline{U}_{out}}{\underline{U}_E} = \frac{j \omega + \frac{R2}{L1} }{j \omega + \frac{R1 + R2}{L1} } = \frac{j \omega - s_{N1} }{j \omega - s_{P1} } \)
Die Übertragungsfunktion setzt sich aus Faktoren (jω - sNi) und (jω - sPi)-1 zusammen.
Das Maß in Dezibel ist definiert als
\( 20 log_{10} \left| \frac{\underline{U}_A}{\underline{U}_E} \right| dB \)
Die Übertragungsfunktion als Maß ist dann:
\( A(j\omega) = 20 log_{10} \left| j \omega + \frac{R2}{L1} \right| dB - 20 log_{10} \left| j \omega + \frac{R1 + R2}{L1} \right| dB \)
Die Übertragungsfunktion stellt das Maß in Dezibel (dB) und die Phase über der logarithmischer Frequenz dar.
Durch die obige Form kann man die Übertragungsfunktion als Maß mit einer logarithmischen Frequenz schnell zeichnen.
Man beachte dass negative Vorzeichen beim Maß für den Nenner.
Jede Übertragungsfunktion wird so umgeformt, dass im Zähler und Nenner ein Polynom von jω steht.
Durch suche der Nullstellen kann man dieses Polynom dann zerlegen.
z.B. (jω)2 + 2 Re jω + Re2 = (jω + Re )2
Die Übertragungsfunktion setzt sich dann aus einzelnen Termen von jω zusammen.
Die einzelnen Terme werden graphisch addiert (subtrahiert).
Da jω in der Elektrotechnik als s abgekürzt wird und der obige Term (jω + sNi) sich wie eine Nullstelle (Ni verhält, ergibt sich der Bezeichner sNi.
Für den Nenner (jω + sPi)-1 ergibt sich eine Polstelle (Pi)
Maße in Dezibel, die man sich merken sollte:
20 dB entsprechen einem Faktor 10.
6 dB entsprechen einem Faktor 2.
3 dB entsprechen einem Faktor \( \sqrt{2} \).
0 dB entsprechen dem Faktor 1.
Durch die obige Form kann man die Übertragungsfunktion als Maß mit einer logarithmischen Frequenz schnell zeichnen.
Man beachte dass negative Vorzeichen beim Maß für den Nenner.
Jede Übertragungsfunktion wird so umgeformt, dass im Zähler und Nenner ein Polynom von jω steht.
Durch suche der Nullstellen kann man dieses Polynom dann zerlegen.
z.B. (jω)2 + 2 Re jω + Re2 = (jω + Re )2
Die Übertragungsfunktion setzt sich dann aus einzelnen Termen von jω zusammen.
Die einzelnen Terme werden graphisch addiert (subtrahiert).
Da jω in der Elektrotechnik als s abgekürzt wird und der obige Term (jω + sNi) sich wie eine Nullstelle (Ni verhält, ergibt sich der Bezeichner sNi.
Für den Nenner (jω + sPi)-1 ergibt sich eine Polstelle (Pi)
Maße in Dezibel, die man sich merken sollte:
20 dB entsprechen einem Faktor 10.
6 dB entsprechen einem Faktor 2.
3 dB entsprechen einem Faktor \( \sqrt{2} \).
0 dB entsprechen dem Faktor 1.
Untersuchung der Übertragungsfunktion als Maß
\( A(j\omega) = 20 log_{10} \left| j \omega + \frac{R2}{L1} \right| dB - 20 log_{10} \left| j \omega + \frac{R1 + R2}{L1} \right| dB \)
Für die Zeichnung untersucht man für jeden Term: jω + Re, ob ω viel größer als der Realteil Re ist oder viel kleiner.
j ω >> Re: \( 20 log_{10} | j \omega | \)
Wenn sich ω um den Faktor 10 ändert, ändert sich das Maß um 20 dB. Eine Gerade mit Steigung 20 dB pro Dekade (Faktor 10).
j ω << Re : \( 20 log_{10} | Re | \)
Der Betrag ist konstant. Eine Gerade mit Steigung 0.
Der Übergang dieser Funktionen passiert, wenn | jω | = Re ist (Eckfrequenz).
3dB Eckfrequenz
Untersuchung von
\( 20 log_{10} \left| j \omega - s_{N1} \right| dB \)
für | jω | = Re
\( 20 log_{10} \left( \sqrt{ Re^2 + Re^2} \right) dB = 20 log_{10} \left( \sqrt{2} \cdot Re \right) dB \)
\( = 20 log_{10} \left( \sqrt{2} \right) dB + 20 log_{10} \left(Re \right) dB \)
\( = 3 dB + 20 log_{10} \left(Re \right) dB \)
Die reale Übertragungsfunktion als Maß weicht an der Eckfrequenz um 3 dB von den idealisierten Geraden ab.
Der Phasengangs der Übertragungsfunktion (06.06.2023)
Untersuchung von
\( \underline{T} (j\omega) = \frac{\underline{U}_{out}}{\underline{U}_E} = \frac{j \omega + Re_Z }{j \omega + Re_N } = \frac{j \omega - s_{N1} }{j \omega - s_{P1} } \)
\( \phi (j\omega) = atan\left(\frac{\omega}{Re_Z}\right) - atan\left(\frac{\omega}{Re_N}\right)\)
j ω >> Re: \( atan\left(\frac{\omega}{Re}\right) = 90° \)
j ω << Re : \( atan\left(\frac{\omega}{Re}\right) = 0° \)
j ω = Re: \( atan\left(\frac{Re}{Re}\right) = 45° \)
Für die Zeichnung untersucht man für jeden Term: jω + Re,
ob ω viel größer als der Realteil Re ist oder viel kleiner.
Für j ω >> Re ist der Winkel konstant 90° (π/2).
Für j ω << Re ist der Winkel konstant 0° (0).
Der Übergang dieser Funktionen passiert, wenn | jω | = Re ist (Eckfrequenz).
Für j ω = Re: ist der Winkel ist 45° (π/4).
Bei einem Faktor 10 für ω ist jω >> Re oder jω << Re.
Man kann beim Zeichnen also die Punkte für f3dB, 1/10 f3dB und 10 f3dB einzeichnen.
Die Umrechnung von Bogenmaß in Grad erfolgt mit:
π = 180°
\( \phi_B = \frac{\phi_{Grad}}{180} \cdot \pi \)
\( \phi_{Grad} = \frac{\phi_B}{\pi} \cdot 180° \)
Für j ω >> Re ist der Winkel konstant 90° (π/2).
Für j ω << Re ist der Winkel konstant 0° (0).
Der Übergang dieser Funktionen passiert, wenn | jω | = Re ist (Eckfrequenz).
Für j ω = Re: ist der Winkel ist 45° (π/4).
Bei einem Faktor 10 für ω ist jω >> Re oder jω << Re.
Man kann beim Zeichnen also die Punkte für f3dB, 1/10 f3dB und 10 f3dB einzeichnen.
Die Umrechnung von Bogenmaß in Grad erfolgt mit:
π = 180°
\( \phi_B = \frac{\phi_{Grad}}{180} \cdot \pi \)
\( \phi_{Grad} = \frac{\phi_B}{\pi} \cdot 180° \)
Entwicklung eines Bode Diagramms
Maß
- Teilfunktionen:
- Faktor K: Gerade
- Nullstelle jω - sni: Parallele Gerade zur x-Achse (20 log(-sni) ) und Knick nach oben (20 dB/dec) bei - sni
- Polstelle jω - spi: Parallele Gerade zur x-Achse (-20 log(-spi) ) und Knick nach unten (20 dB/dec) bei - spi
- Punktweise Addition
Winkel
- Teilfunktionen:
- Nullstelle jω - sni: 0° bis - sni/10, +45° bei - sni und 90° ab - sni·10
- Polstelle jω - spi: 0° bis - spi/10, -45° bei - spi und -90° ab - spi·10
- Punktweise Addition
Übertragungsfunktion und Maß des Beispiels
|
\( \frac{U_{out}}{U_E} = \frac{j \omega + \frac{R2}{L1} }{j \omega + \frac{R1 + R2}{L1} }\) \( 20 log_{10} | j \omega + \frac{R2}{L1} | \) \( - 20 log_{10} | {j \omega + \frac{R1 + R2}{L1} } | \) \( \frac{R2}{2 \pi L1 } = 86 kHz \) \( \frac{R1 + R2}{2 \pi L1} = 934 kHz \) \( 20 log | \frac{R2}{L1} | = 114 dB \) und \( - 20 log | {\frac{R1 + R2}{L1} } | = - 135 dB \) |
\( \frac{R2}{L1} = 533E3 s^{-1} \)
\( \frac{R1 + R2}{L1} = 5866E3 s^{-1} \)
Mit der Normierung auf s-1 kann man den 10er Logarithmus berechnen:
\( 20 log (\frac{R2}{L1}) = 135 dB \)
\( 20 log (\frac{R1 + R2}{L1}) = 114 dB \)
Man kann nun die 2 Punkte eintragen:
P1(533E3 s-1, 135 dB) und P2(5866E3 s-1, 114 dB)
Zwischen diesen Punkten liegt näherungsweise eine Gerade mit Steigung 20dB/Dekade (Faktor 10).
Rechts und links der Punkte ist das Maß konstant (jω<<Re).
\( \frac{R1 + R2}{L1} = 5866E3 s^{-1} \)
Mit der Normierung auf s-1 kann man den 10er Logarithmus berechnen:
\( 20 log (\frac{R2}{L1}) = 135 dB \)
\( 20 log (\frac{R1 + R2}{L1}) = 114 dB \)
Man kann nun die 2 Punkte eintragen:
P1(533E3 s-1, 135 dB) und P2(5866E3 s-1, 114 dB)
Zwischen diesen Punkten liegt näherungsweise eine Gerade mit Steigung 20dB/Dekade (Faktor 10).
Rechts und links der Punkte ist das Maß konstant (jω<<Re).
Übertragungsfunktion eines Netzes (26.05.2025)
|
Gesucht ist die Übertragungsfunktion folgenden Netzes:
Wir wollen den Amplituden und Phasengang der Spannung U(j ω),
den Frequenzgang F(jω) der auf die Quellenspannung bezogenen Spannung
bestimmen.
\( \underline{F} \left( j \omega \right) = \frac{\underline{U}_A \left( j \omega \right)}{\underline{U}_E \left( j \omega \right)} = \) Spannungsteilerregel, da der Strom der Gleiche ist: \( \underline{I} = \frac{ \underline{U}_E}{R_1 + \frac{1}{\frac{1}{R_2} + j \omega C_1}} = \underline{U}_A \left( \frac{1}{R_2} + j \omega C_1 \right) \) \( \underline{F} \left( j \omega \right) = \frac{\underline{U}_A}{\underline{U}_E} = \frac{ 1}{ \left( R_1 + \frac{1}{\frac{1}{R_2} + j \omega C_1} \right) \left( \frac{1}{R_2} + j \omega C_1 \right)} \) Die Brüche unter dem Bruchstrich sollen eliminiert werden: Ausmultiplizieren \( \underline{F} \left( j \omega \right) = \frac{\underline{U}_A}{\underline{U}_E} = \frac{ 1}{ \frac{R_1}{R_2} + j \omega C_1 R_1 + 1} = \frac{ 1}{ j \omega C_1 R_1 + \frac{R_1}{R_2} + 1} = \frac{ 1}{C_1 R_1} \frac{ 1}{ j \omega + \frac{R_1 + R_2 }{C_1 R_1 R_2}} \) \( K = \frac{ 1}{C_1 R_1} \) \( s_{p1} = - \frac{R_1 + R_2 }{C_1 R_1 R_2} \) Amplitudengang: \( U_A ( \omega ) = U_E K \frac{1}{\sqrt{ \left( \frac{R_1 + R_2 }{C_1 R_1 R_2} \right)^2 + \omega^2 } } \) Phasengang: \( \phi_A ( \omega ) = \phi_E - arctan \left( \frac{\omega}{\frac{R_1 + R_2 }{C_1 R_1 R_2}} \right) = \phi_E - arctan \left( \frac{\omega C_1 R_1 R_2 }{R_1 + R_2 } \right) \) |
Logarithmische Größenverhältnisse:
- Frequenz \( \omega \) und der Betrag werden logarithmisch aufgetragen.
Vorteile: - Größen mit stark unterschiedlichen Zahlenwerten können grafisch so veranschaulicht werden, dass die Ablesegenauigkeit dem jeweiligen Wert der Größe entspricht.
- Die Darstellungen der Frequenzabhängigkeit in Diagrammen führen bei der Verwendung logarithmierter Größenverhältnisse häufig auf Geradenabschnitte.
- Multiplikationen der ursprünglichen Größen gehen in Additionen der logarithmierten Größen über und können daher leichter ausgeführt werden.
- Größenverhältnis ist der dimensionslose Quotient
zweier gleichartiger physikalischer Größen
Ansonsten normiert man mit 1 V, 1 A, 1 Ω - Man kann mit verschiedenen Größen normieren
- Es können verschiedene Basen für den Logarithmus verwendet werden
Die Logarithmusfunktion (Wikipedia)
- Basis des Logarithmus:
- Basis 10: lg, log, log10
- Basis e (Eulersche Zahl): ln
- Logarithmus:
- Mit welcher Zahl muss ich die Basis potenzieren um x zu erhalten
- y = log x 10y = x
- y = ln x ey = x
- Rechnen
- log(ab) = log a + log b
- log(a2) = log(aa) = loga + loga = 2 log a
Logarithmische Größenverhältnisse in Dezibel
Energiegrößen und Feldgrößen
Logarithmierte Größenverhältnisse in Dezibel
Quotient zweier Wirkleistungen
\( a_p = 10 \cdot log \frac{P_1}{P_2} dB = 20 \cdot log \frac{U_1}{U_2} dB \)
Mit \( P = \frac{U^2}{R} \)
Zusatz dB Dezibel Dimensionslos, wie rad
Zahlenwerte und Dezibel
| Faktor | log10 | dB | ln |
| 1 | 0 | 0 | 0 |
| 2 | 0.3 | 6 | 0.69 |
| 2.72 | 0.43 | 8.6 | 1 |
| 7.39 | 0.87 | 17.4 | 2 |
| 10 | 1 | 20 | 2.3 |
| 100 | 2 | 40 | 4.6 |
Beispiel Dezibel
Wir wollen das Verhältnis der Leistungen Pl = 20 W und P2 = 50 mW in dB angeben:
\( a_p = 10 lg \frac{P_1}{P_2} = 10 lg \frac{20 W}{0.05 W} = 10 lg 400
\)
\( a_p = 10 lg ( 2 \cdot 2 \cdot 100 ) = 10 \cdot ( 0.3 + 0.3 + 2) dB = 26 dB \)
\( a_p = 10 lg ( 2 \cdot 2 \cdot 100 ) = 10 \cdot ( 0.3 + 0.3 + 2) dB = 26 dB \)
Logarithmische Größenverhältnisse in Neper
Hier ist die Basis e und der Zusatz Np (Neper)
\( a_p = 0.5 ln \frac{P_1}{P_2} Np \)
Umrechnung Neper und Dezibel
Direkte Proportionalität
1 Np = 8.69 dB
1 dB = 0.115 Np
Pegel (Level)
- Absoluter Pegel
- Feste Bezugsgröße die nicht vom Betriebszustand abhängig ist
- Die Bezugsgröße muss genannt werden.
- Relativer Pegel
- Differenz der Pegel zwischen Messstelle und Bezugsstelle
- Angabe in dBr
- Relativer Pegel kann auch ohne Bezugsgröße verwendet werden.
- Der Pegelangabe in dBm liegt die Bezugsleistung 1 mW zu Grunde. Sollen Strom- oder Spannungspegel in dBm angegeben werden, so wird als Bezugswiderstand in der Hochfrequenztechnik 50 Ω und in der Telefon- und Weit-verkehrstechnik 600 Ω verwendet. Eine Angabe in dBm0 weist durch die nachgestellte 0 darauf bin, dass dieser Pegel in dBm an einer Bezugsstelle im Netz auftritt. In der Telefontechnik ist die Bezugsstelle z. B. der Eingang zu einer Frequenzmultiplexeinrichtung. Der genormte Pegel an dieser Stelle ist -15 dBm0.
- In der Fernsehtechnik werden Pegel oft in dBµV angegeben. Die Bezugsgröße ist die Spannung 1µV. Strom und Leistungspegel werden mit dem Widerstand 75 Ω gebildet.
- Mit der Pegelangabe in dBc beschreibt man die relative Größe von Seitenbändern eines modulierten Trägers. Der Zusatz "c" weist auf den Träger (carrier) hin.
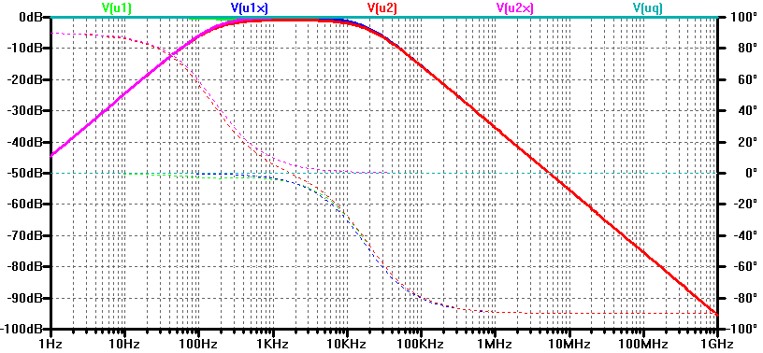
Beispiel Übertragungsfunktion
Wir wollen den Übertragungsfaktor T(jω) bestimmen.
Ein belasteter Spannungsteiler.
Das Problem wird zerlegt in die Bestimmung von \( \underline{U}_1 \) und \( \underline{U}_2 \)
\( \underline{T}(j \omega ) = \frac{\underline{U}_2}{\underline{U}_q} = \frac{\underline{U}_2}{\underline{U}_1} \frac{\underline{U}_1}{\underline{U}_q} \)
Ansatz für die Spannungen
\( \frac{\underline{U}_2}{R_2} = \frac{\underline{U}_1}{R_2 + \frac{1}{j \omega C_2}} = \frac{\underline{U}_1}{\underline{Z}_2} \)
\( \frac{\underline{U}_q}{R_1 + \frac{1}{j \omega C_1 + \frac{1}{R_2 + \frac{1}{j \omega C_2}}}} = \frac{\underline{U}_1}{\frac{1}{j \omega C_1 + \frac{1}{R_2 + \frac{1}{j \omega C_2}}}} \)
\( \frac{\underline{U}_q}{R_1 + \underline{Z}_1} = \frac{\underline{U}_1}{\underline{Z}_1} \)
\( \frac{\underline{U}_1}{\underline{U}_q} = \frac{\underline{Z}_1}{R_1 + \underline{Z}_1} = \frac{1}{R_1 \underline{Y}_1 + 1 } \)
\( \underline{Z}_2 = R_2 + \frac{1}{j \omega C_2} = \frac{j \omega C_2 R_2 + 1}{j \omega C_2} \)
\( \underline{Y}_1 = j \omega C_1 + \frac{1}{R_2 + \frac{1}{j \omega C_2}} = j \omega C_1 + \frac{j \omega C_2}{j \omega C_2 R_2 + 1} \)
\( \frac{\underline{U}_2}{\underline{U}_1} = \frac{R_2}{\underline{Z}_2} = \frac{j \omega C_2 R_2}{j \omega C_2 R_2 + 1} \)
\( \frac{\underline{U}_1}{\underline{U}_q} = \frac{1}{R_1 \underline{Y}_1 + 1 } = \frac{1}{R_1 \left( j \omega C_1 + \frac{j \omega C_2}{j \omega C_2 R_2 + 1} \right) + 1 } \)
\( \underline{T}(j \omega ) = \frac{R_2 }{\underline{Z}_2} \frac{1}{\frac{R_1}{\underline{Z}_1}+1} = \frac{j \omega C_2 R_2}{j \omega C_2 R_2 + 1} \frac{1}{R_1 \left( j \omega C_1 + \frac{j \omega C_2}{j \omega C_2 R_2 + 1} \right) + 1 } \)
\( \underline{T}(j \omega ) = \frac{j \omega C_2 R_2} {\left( R_1 j \omega C_1 + 1 \right) \left( j \omega C_2 R_2 + 1 \right) + j \omega C_2 R_1} \)
\( \underline{T}(j \omega ) = C_2 R_2 \frac{j \omega } {\left( j \omega \right)^2 R_1 C_1 R_2 C_2 + j \omega \left( R_1 C_1 + C_2 \left( R_2 + R_1 \right) \right) + 1} \)
\( \underline{T}(j \omega ) = \frac{C_2 R_2}{R_1 C_1 R_2 C_2} \frac{j \omega } {\left( j \omega \right)^2 + \frac{ j \omega \left( R_1 C_1 + C_2 \left( R_2 + R_1 \right)\right) + 1}{R_1 C_1 R_2 C_2} } \)
\( \underline{T}(j \omega ) = \frac{1}{R_1 C_1} \frac{j \omega } {\left( j \omega \right)^2 + j \omega \frac{R_1 C_1 + C_2 \left( R_2 + R_1 \right)}{R_1 C_1 R_2 C_2} + \frac{1}{R_1 C_1 R_2 C_2} } \)
Mit
\( b = \frac{R_1 C_1 + C_2 \left( R_2 + R_1 \right)}{R_1 C_1 R_2 C_2} \)
\( c = \frac{1}{R_1 C_1 R_2 C_2} \)
werden die Nullstellen des Nenners ermittelt:
\( \left( j \omega \right)^2 + j \omega b + c = 0 \)
\( j \omega_{1,2} = - \frac{1}{2} b \pm \sqrt{\frac{1}{4}b^2 - c} \)
Pole:
sp1 = -3.82 · 106s-1
sp2 = -2.62 · 107s-1
Nullstelle: ω = 0 s-1
\( K = \frac{1}{R_1 C_1} = 10^{7} s^{-1} \)
\( \underline{T}(j \omega ) = K \frac{j \omega - 0} {\left( j \omega - s_{p1} \right) \left( j \omega - s_{p2} \right)} \)
\( \underline{T}(j \omega ) = 10^{7} s^{-1} \frac{j \omega - 0} {\left( j \omega + 3.82 \cdot 10^{6}s^{-1} \right) \left( j \omega + 2.62 \cdot 10^{7}s^{-1} \right)} \)
Vergleich mit dem Frequenzgang der Teilschaltungen:
\( \frac{\underline{U}_{1x}}{\underline{U}_{q}} = \frac{1}{\left( R_1 + \frac{1}{j \omega C_1} \right) j \omega C_1 } \)
\( \frac{\underline{U}_{1x}}{\underline{U}_{q}} = \frac{1}{ j \omega C_1 R_1 + 1 } \)
Pole:
sp1x = -1 · 107s-1
sp2x = -1 · 107s-1
Beispiel Übertragungsfunktion
| |
|

|
b = 1.07E5
c = 9.35E7
f1 = 140 Hz
f2 = 17 kHz
c = 9.35E7
f1 = 140 Hz
f2 = 17 kHz
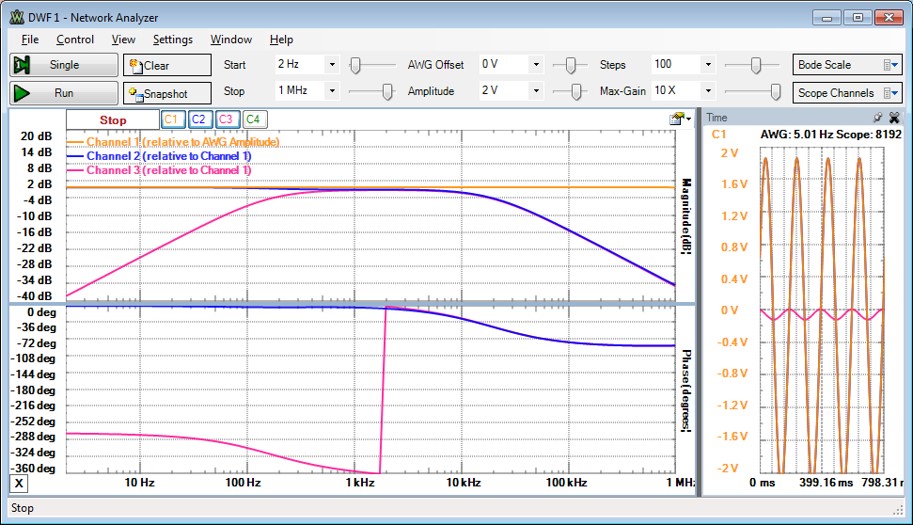
Übertragungsfunktion Verifikation mit LTSPICE
|
3.1. Geben Sie die Pole und Nullstellen der Übertragungsfunktion \( \frac{\underline{U}_1}{\underline{U}_q} \) von folgendem Netz an. \( R_1 = 10 \Omega, R_2 = 2490 \Omega, L = 40 mH, C = 40nF\). 3.2. Geben Sie die Spannung \( \underline{U}_1 \) für \( \omega = 0 \) und \( \omega \rightarrow \infty \) an. |
Lösung:
\( \frac{\underline{U}_1}{\underline{U}_q} = \frac{ R_1 + j \omega L_1}{\frac{1}{j \omega C} + R_2 + R_1 + j \omega L_1} \)
\( \frac{\underline{U}_1}{\underline{U}_q} = L_1 \frac{\left(j \omega + \frac{R_1}{L_1}\right) j \omega} {(j \omega)^2 L_1 + j \omega (R_1 + R_2) + \frac{1}{C}} \)
\( \frac{\underline{U}_1}{\underline{U}_q} = \frac{\left(j \omega + \frac{R_1}{L_1}\right) j \omega} {(j \omega)^2 + j \omega \frac{R_1 + R_2}{L_1} + \frac{1}{C L_1}} \)
\( j \omega_{1,2} = \frac{R_1 + R_2}{2 L_1} \pm \sqrt{\frac{(R_1 + R_2)^2}{4 L_1^2} - \frac{1}{C L_1}} \)
\( j \omega_{1,2} = \frac{R_1 + R_2}{2 L_1} \pm \sqrt{\frac{(R_1 + R_2)^2}{4 L_1^2} - \frac{1}{C L_1}} \)
sN1 = 0
sN2 = -250 s-1
fsN2 = 39.8 Hz
sP1 = -50000 s-1
sP2 = -12500 s-1
fsP1 = 7.96 kHz
fsP2 = 2
kHz
\( U_1 (\omega = 0) = 0 V \)
\( U_1 (\omega \rightarrow \infty) = U_q \)
Man kann in LTSPICE gesteuerte Quellen mit einer Laplace-Gleichung, einer Übertragungsfunktion eingeben und so den Ansatz und alle Rechenschritte überprüfen.
Zusammenfassung und nächstes Mal
- Übertragungsfunktion, Bode Diagramm
- Maß, Dezibel, Phase
- Konstruktion der Kurven
- Vierpole