Grundlagen Elektrotechnik 2 (GET2) 19 Vierpole Prof. Dr. Jörg Vollrath 18 Bode Diagramm

Bode Diagramm Regeln (13.06.2023)

• Maß Amplitudengang
• Ab der Eckfrequenz(Nullstellen/Pole) steigt die Kurve mit 20dB pro Dekade an (Nullstelle) oder fällt mit 20dB pro Dekade ab (Pol)
• Basis ist der Faktor 20 log k bzw. 20log|-S_N|, -20log|-S_P|
• Für S_N oder S_P=0 bestimmt man das Maß für ω=1
• Phasengang
• Zwischen 1/10 Eckfrequenz und 10 %middot; Eckfrequenz steigt die Phase von 0° auf 90° an (Nullstelle) oder fällt von 0° auf -90°(Pol). Bei der Eckfrequenz ist die Phase 45°(Nullstelle) oder -45° (Pol)
• Die Gesamtkurve ergibt sich aus der Überlagerung der einzelnen Kurven.

Rückblick und Übersicht

• Auswertung: Ortskurve, Bode Diagramm
• Bode Diagramm
• Manuell, Excel, SPICE (.ac)

• Vierpol und zweitor im Netzwerk
• Charakteristische Matrix
• Matrizenrechnung
• Bestimmung der Matrizenwerte

Ziele

• Sie können ein Zweitor und einen Vierpol definieren.
• Sie können Zweitore zur Netzwerkberechnung verwenden.
• Sie können die charakteristischen Matrizen für Zweitore aufstellen.
• Sie können Ersatzschaltbilder von Zweitoren berechnen.
• Sie können die Übertragungsfunktion bei der Zusammenschaltung von Zweitoren berechnen.

Einführungl

• Grundaufgabe der Elektrotechnik
• Energieübertragung: Erzeuger -> Verbraucher
• Energietechnik: Große Energie
• Kraftwerk -> Haushalt
• Informationsübertragung: kleine Energie für Nachrichten
• Sender Kabel/Luft Empfänger
• Man interessiert sich nicht für die Vorgänge auf dem Weg, sondern nur für die Beziehung zwischen Spannungen und Ströme am Eingang und am Ausgang
• Man interessiert sich für das Klemmenverhalten des Übertragungsgliedes
• Zweitortheorie befasst sich mit der Beschreibung des Zusammenhangs der Eingangs und Ausgangsgrößen.

Zweitor mit symmetrischen Pfeilen

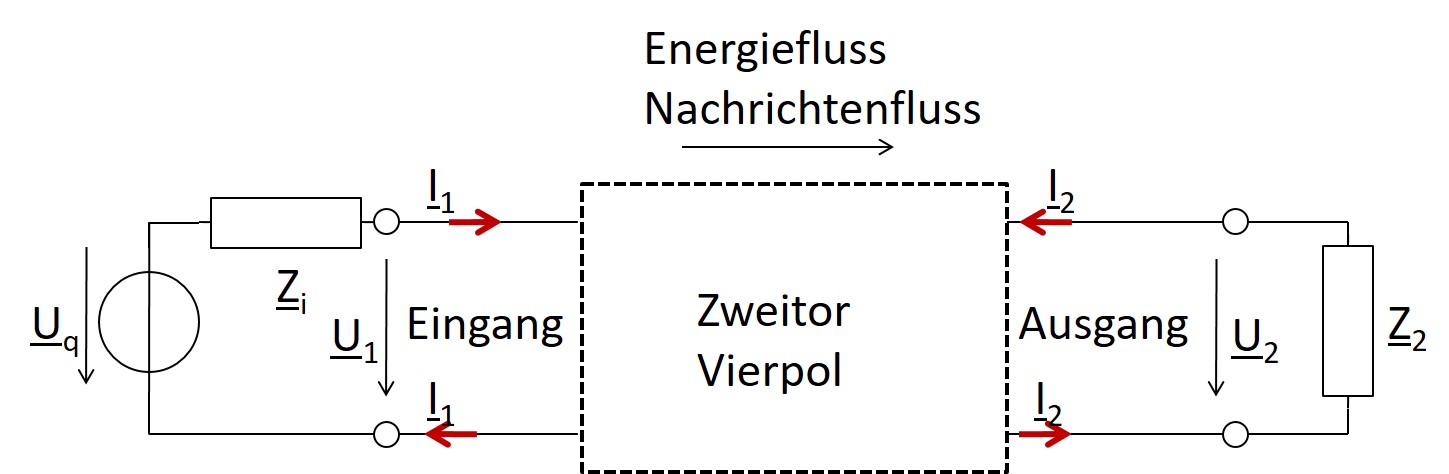
• Vier Anschlussklemmen: Vierpol
• 2 Tore: Eingang (Input) und Ausgang (Output)
• Klemmenpaar
• Der Strom, der über eine Klemme hineinfließt kommt aus der anderen heraus (Torbedingung)

Formen der Zweitormatrix

Widerstandsmatrix Z	Reihen-Parallel-Matrix H
\( \left( \begin{array}{r} \underline{U}_1 \\ \underline{U}_2 \\ \end{array} \right) = \left( \begin{array}{rr} \underline{Z}_{11} & \underline{Z}_{12} \\ \underline{Z}_{12} & \underline{Z}_{22} \\ \end{array} \right) \left( \begin{array}{r} \underline{I}_1 \\ \underline{I}_2 \\ \end{array} \right) \)	\( \left( \begin{array}{r} \underline{U}_1 \\ \underline{I}_1 \\ \end{array} \right) = \left( \begin{array}{rr} \underline{H}_{11} & \underline{H}_{12} \\ \underline{H}_{12} & \underline{H}_{22} \\ \end{array} \right) \left( \begin{array}{r} \underline{I}_1 \\ \underline{U}_2 \\ \end{array} \right) \)
Leitwertmatrix Y	Parallel-Reihen-Matrix P/G
\( \left( \begin{array}{r} \underline{I}_1 \\ \underline{I}_2 \\ \end{array} \right) = \left( \begin{array}{rr} \underline{Y}_{11} & \underline{Y}_{12} \\ \underline{Y}_{12} & \underline{Y}_{22} \\ \end{array} \right) \left( \begin{array}{r} \underline{U}_1 \\ \underline{U}_2 \\ \end{array} \right) \)	\( \left( \begin{array}{r} \underline{I}_1 \\ \underline{U}_2 \\ \end{array} \right) = \left( \begin{array}{rr} \underline{P}_{11} & \underline{P}_{12} \\ \underline{P}_{12} & \underline{P}_{22} \\ \end{array} \right) \left( \begin{array}{r} \underline{U}_1 \\ \underline{I}_2 \\ \end{array} \right) \)
Kettenmatrix A	Inverse Kettenmatrix B
\( \left( \begin{array}{r} \underline{U}_1 \\ \underline{I}_1 \\ \end{array} \right) = \left( \begin{array}{rr} \underline{A}_{11} & \underline{A}_{12} \\ \underline{A}_{12} & \underline{A}_{22} \\ \end{array} \right) \left( \begin{array}{r} \underline{U}_2 \\ - \underline{I}_2 \\ \end{array} \right) \)	\( \left( \begin{array}{r} \underline{U}_2 \\ \underline{I}_2 \\ \end{array} \right) = \left( \begin{array}{rr} \underline{B}_{11} & \underline{B}_{12} \\ \underline{B}_{12} & \underline{B}_{22} \\ \end{array} \right) \left( \begin{array}{r} \underline{U}_1 \\ - \underline{I}_1 \\ \end{array} \right) \)

Wie charakterisiere ich ein Zweitor?

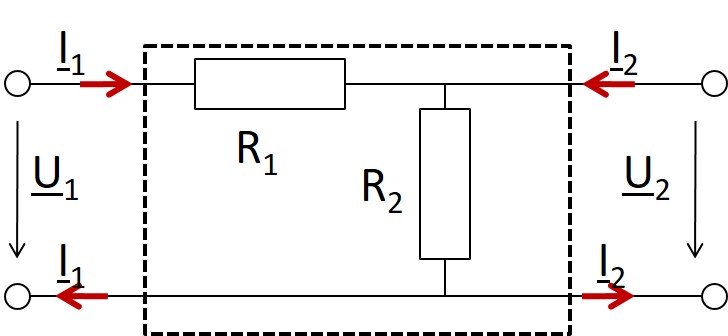
Maschengleichung: \( \underline{U}_2 = R_2 \cdot \underline{I}_1 + R_2 \cdot \underline{I}_2 \) \( \underline{U}_1 = (R_1 + R_2) \cdot \underline{I}_1 + R_2 \cdot \underline{I}_2 \)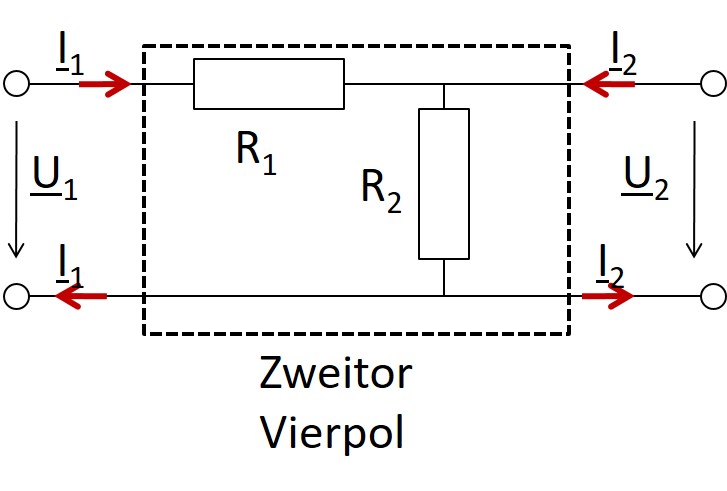

\( \left( \begin{array}{r} \underline{U}_1 \\ \underline{U}_2 \\ \end{array} \right) = \left( \begin{array}{rr} R_1 + R_2 & R_2 \\ R_2 & R_2 \\ \end{array} \right) \left( \begin{array}{r} \underline{I}_1 \\ \underline{I}_2 \\ \end{array} \right) \)

\( \left( \begin{array}{r} \underline{U}_1 \\ \underline{U}_2 \\ \end{array} \right) = \left( \begin{array}{rr} \underline{Z}_{11} & \underline{Z}_{12} \\ \underline{Z}_{12} & \underline{Z}_{22} \\ \end{array} \right) \left( \begin{array}{r} \underline{I}_1 \\ \underline{I}_2 \\ \end{array} \right) \)

Wie bestimmt man die einzelnen Werte der Matrizen?

\( \left( \begin{array}{r} \underline{U}_1 \\ \underline{U}_2 \\ \end{array} \right) = \left( \begin{array}{rr} \underline{Z}_{11} & \underline{Z}_{12} \\ \underline{Z}_{12} & \underline{Z}_{22} \\ \end{array} \right) \left( \begin{array}{r} \underline{I}_1 \\ \underline{I}_2 \\ \end{array} \right) \) Eine Spannung an einem Tor anlegen Das andere Tor offen lassen ( I = 0 ) Strom und Spannung messen

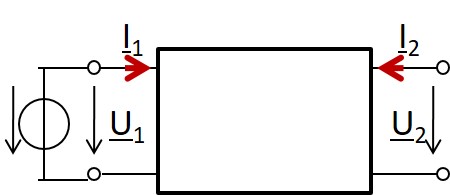\( \underline{Z}_{11} = \left. \frac{\underline{U}_{1}}{\underline{I}_{1}} \right\vert_{\underline{I}_2 = 0} \) \( \underline{Z}_{21} = \left. \frac{\underline{U}_{2}}{\underline{I}_{1}} \right\vert_{\underline{I}_2 = 0} \)

Wie bestimmt man die einzelnen Werte der Matrizen?

\( \left( \begin{array}{r} \underline{U}_1 \\ \underline{U}_2 \\ \end{array} \right) = \left( \begin{array}{rr} \underline{Z}_{11} & \underline{Z}_{12} \\ \underline{Z}_{12} & \underline{Z}_{22} \\ \end{array} \right) \left( \begin{array}{r} \underline{I}_1 \\ \underline{I}_2 \\ \end{array} \right) \) Eine Spannung an einem Tor anlegen Das andere Tor offen lassen ( I = 0 ) Strom und Spannung messen

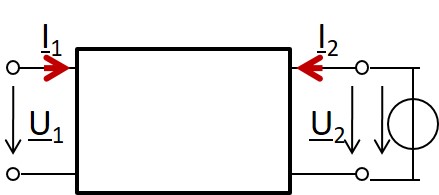\( \underline{Z}_{12} = \left. \frac{\underline{U}_{1}}{\underline{I}_{2}} \right\vert_{\underline{I}_1 = 0} \) \( \underline{Z}_{22} = \left. \frac{\underline{U}_{2}}{\underline{I}_{2}} \right\vert_{\underline{I}_1 = 0} \)

Beispiel: Z-Matrix

R1=100Ω, R2=200Ω Bestimmen Sie die Z Parameter. Das Zweitor wird an eine ideale Stromquelle von 10mA angeschlossen. Berechnen Sie die Spannung U2. Am Ausgang wird ein Strom von 2mA entnommen. Berechnen Sie Eingangs- und Ausgangsspannung.

Matrixoperationen

Multiplikation

\( \underline{Z}_1 \cdot \underline{Z}_2 = \left( \begin{array}{rr} \underline{Z}_{111} \cdot \underline{Z}_{211} + \underline{Z}_{112} \cdot \underline{Z}_{211} & \underline{Z}_{111} \cdot \underline{Z}_{212} + \underline{Z}_{112} \cdot \underline{Z}_{212} \\ \underline{Z}_{121} \cdot \underline{Z}_{211} + \underline{Z}_{122} \cdot \underline{Z}_{211} & \underline{Z}_{121} \cdot \underline{Z}_{212} + \underline{Z}_{122} \cdot \underline{Z}_{212} \\ \end{array} \right) \)

Determinante

\( det \underline{Z} = \left| \begin{array}{rr} \underline{Z}_{11} & \underline{Z}_{12} \\ \underline{Z}_{21} & \underline{Z}_{22} \\ \end{array} \right| = \underline{Z}_{11} \cdot \underline{Z}_{22} - \underline{Z}_{12} \cdot \underline{Z}_{21} \)

Weitere Folien

Wikipedia Zweitor

• Lösung
• Umrechnung der Matrizen (Wikipedia)
• Matrizen: Addition, Multiplikation, Inverse
• Determinante
• Kettenschaltung
• Beispiel Kettenschaltung Spannungsteiler

Beispiel: Kettenschaltung Spannungsteiler

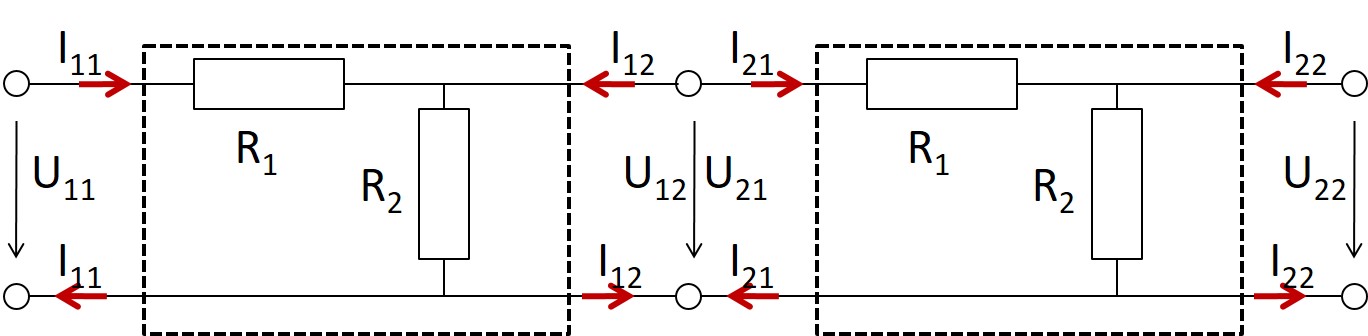
Zwei gleiche Zweitore mit den Widerständen R1=100Ω und R2=50Ω werden in Kette geschaltet. Geben sie die Kettenmatrix der Gesamtschaltung an.
Wie gross ist U11, wenn U22=1V ist?
Wie gross ist der Eingangswiderstand?
Durch Erstellen der einzelnen Matrizen und Rechnung für die Kettenschaltung.

Beispiel: Z-Matrix RC

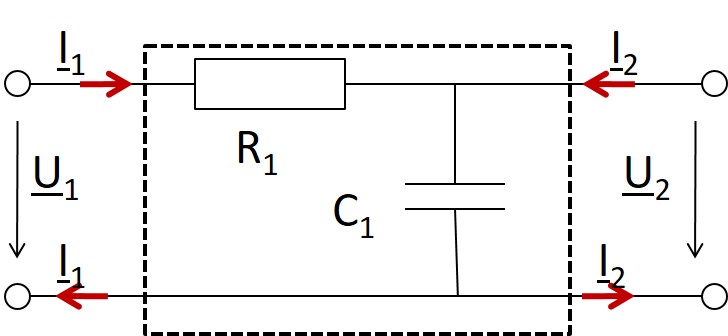
R1=100Ω, C1=45nF Bestimmen Sie die Z Parameter. Das Zweitor wird an eine ideale Stromquelle von 10mA und 20kHz angeschlossen. Berechnen Sie die Spannung U2.

Zusammenfassung und nächstes Mal

• Vierpole
• Ein Zweitor hat vier Klemmen.
• Wir betrachten lineare Zweitore.
• Es gibt Z,Y,H,P,A Matrizen die den Zusammenhang zwischen Eingangsgrößen U1, I1 und Ausgangsgrößen U2, I2 beschreiben.
• Umrechnungstabelle
• Zusammenschaltung -> Matrixrechnung
• Multiplikation, Addition
• Reihenschaltung, Kettenschaltung
• Wir können die einzelnen Koeffizienten der Matrix Messtechnisch bestimmen.
• Achtung: Torbedingung
• Direkte Verbindung (Kurzschluss) zwischen einer Eingangs- und einer Ausgangsklemme.


• Filter
20 Filter