Grundlagen Elektrotechnik 2 (GET2)20 FilterProf. Dr. Jörg Vollrath19 Vierpole 24 Transformator |

|
Video GET2 01 Einführung kompakt
Video der 19. Vorlesung 8.6.2021
|
Länge: 1:22:04 |
0:0:0 Evaluierung 0:0:0 Differenzverstärker 0:2:0 Eingangs und Ausgangswiderstand |
Inhalt Filternetze
- Grenzfrequenz
- Leistungsbetrachtung, Filter (Ordnungszahl)
- Tiefpass
- Idealer Tiefpass, Erster Ordnung , Beispiel 6.20
- Hochpass
- Elementarer Hochpass, Erster Ordnung, Beispiel 6.21, Praxisbezug
- Bandpass
- Untere, obere Grenzfrequenz, Polgüte, (normierte) Verstimmung, Beispiel, Praxisbezug
- Bandsperre
- Allpass
- Filter höherer Ordnung
Filter für Funkanwendungen (WLAN, Bluetooth, AM, FM, DAB) könnten noch vorgestellt werden.
Lautstärkepegel

Wikipedia
Die y-Achse gibt den Wertebereich an: 140 dB entsprechen ENOB = 140 dB /6 dB = 24 Bit.
Die x-Achse zeigt den hörbaren Frequenzbereich von 20 Hz bis 20 kHz.
Ein MP3 Stück (MPEG Audio layer 1/2 (mpga) hat z.B. eine Abtatsrate von 44100 Hz, 32 Bits pro Sample (16 Bit pro Kanal?) und eine Bitrate von 256 kBit/s. Es liegt eine Kompression von 44100 * 32 / 256 / 1024 = 5.5 vor.
Die x-Achse zeigt den hörbaren Frequenzbereich von 20 Hz bis 20 kHz.
Ein MP3 Stück (MPEG Audio layer 1/2 (mpga) hat z.B. eine Abtatsrate von 44100 Hz, 32 Bits pro Sample (16 Bit pro Kanal?) und eine Bitrate von 256 kBit/s. Es liegt eine Kompression von 44100 * 32 / 256 / 1024 = 5.5 vor.
Lautsprecherweiche
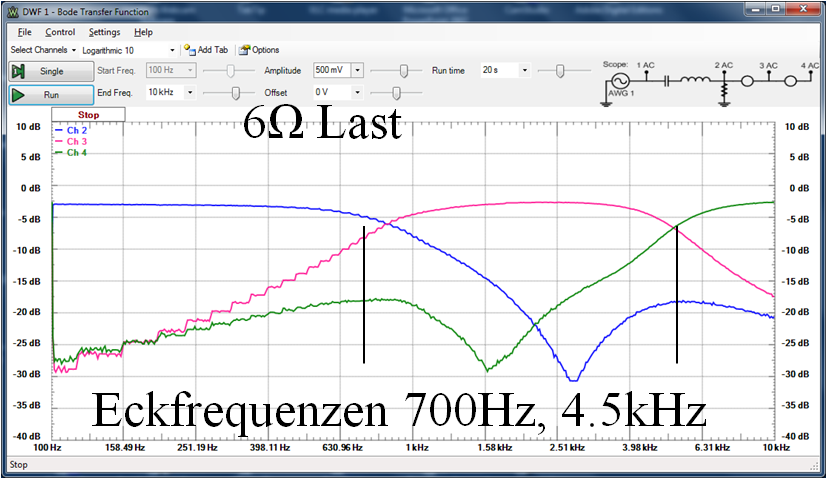
|  Sinuslive 3-Wege-Frequenzweiche CR345 |
|
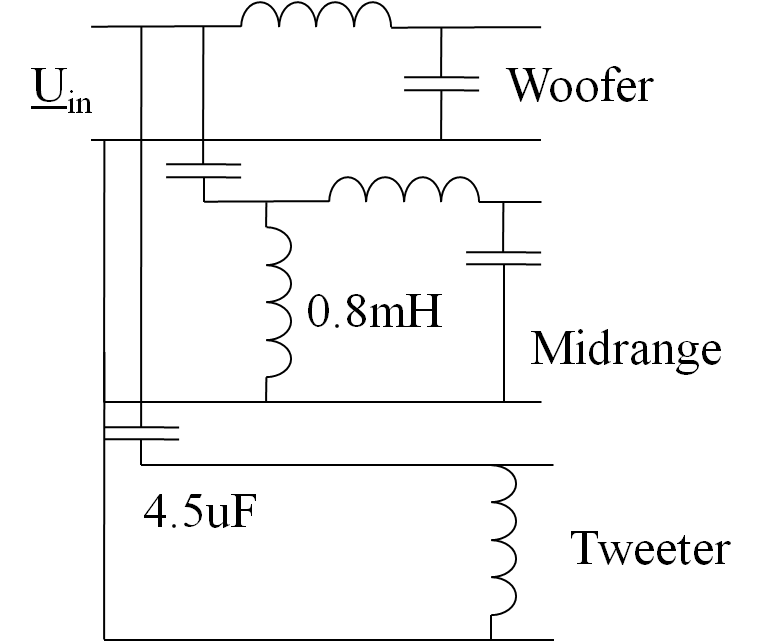 |
Ziele
- die Begriffe 3-dB-Grenzfrequenz, Durchlass- und Sperrbereich erläutern.
- die Begriffe untere und obere Grenzfrequenz, Sperrfrequenz und Übergangsbereich anhand einer Skizze erklären.
- angeben, wie die Ordnungszahl eines Filters definiert ist.
- den Frequenzgang des Übertragungsfaktors der vier idealen Filterarten skizzieren.
- die Forderungen an die Übertragungsfunktionen realer Filter und die Lage ihrer Pol- und Nullstellen nennen.
- je eine Schaltung für einen elementaren Hochpass, Tiefpass, Bandpass und eine elementare Bandsperre angeben und jeweils die 3-dB-Grenzfrequenzen berechnen.
- die vorgenannten elementaren Filter dimensionieren.
Ziele
- die Gleichungen für die Bandbreite, Bandmittenfrequenz und Verstimmung angeben.
- die Resonanzüberhohung und die Güte eines Reihen-bzw. Parallelschwingkreises berechnen.
- die Lage der Pole und Nullstellen eines Allpasses skizzieren und mit ihnen den Betrag und den Winkel des Übertragungsfaktors berechnen.
- die Schaltung eines Allpasses erster Ordnung angeben.
- zeigen, wie durch Frequenztransformation die Übertragungsfunktion eines Tiefpasses in die eines Hochpasses überführt werden kann.
- erläutern, was man unter einem Polynomfilter versteht.
Filtersystemsicht
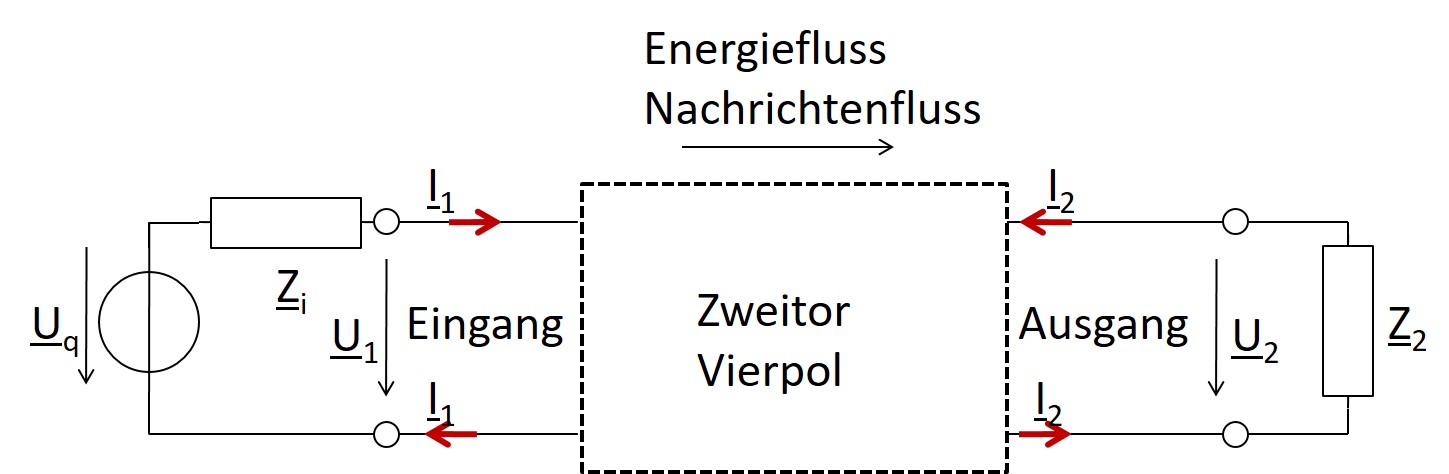
Die Wirkleistung an einem Verbraucher ist frequenzabhängig.
Es gibt eine maximale Wirkleistung Pmax.
- Durchlassbereich (pass band):
P(ω) > Pmax/2 - Sperrbereich (stop band):
P(ω) < Pmax/2 - Grenzfrequenz (cutoff frequency) fg: P(ωg)/Pmax = 1/2
Filter
|
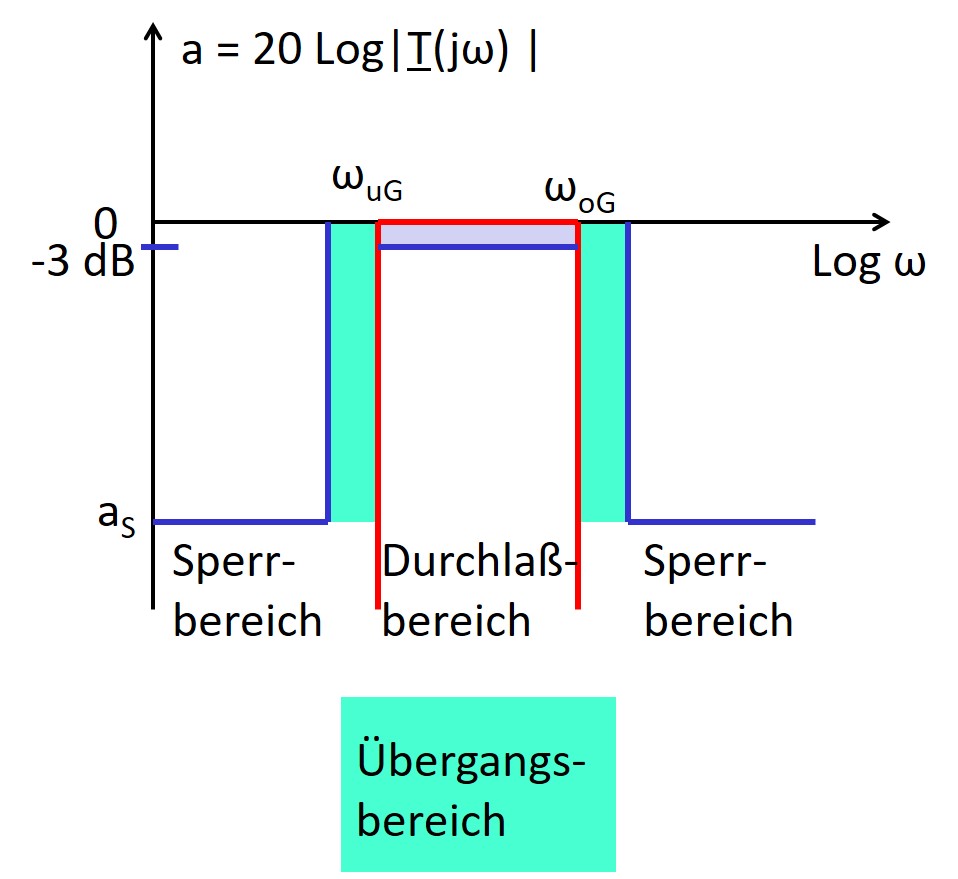 |
Filtervariationen
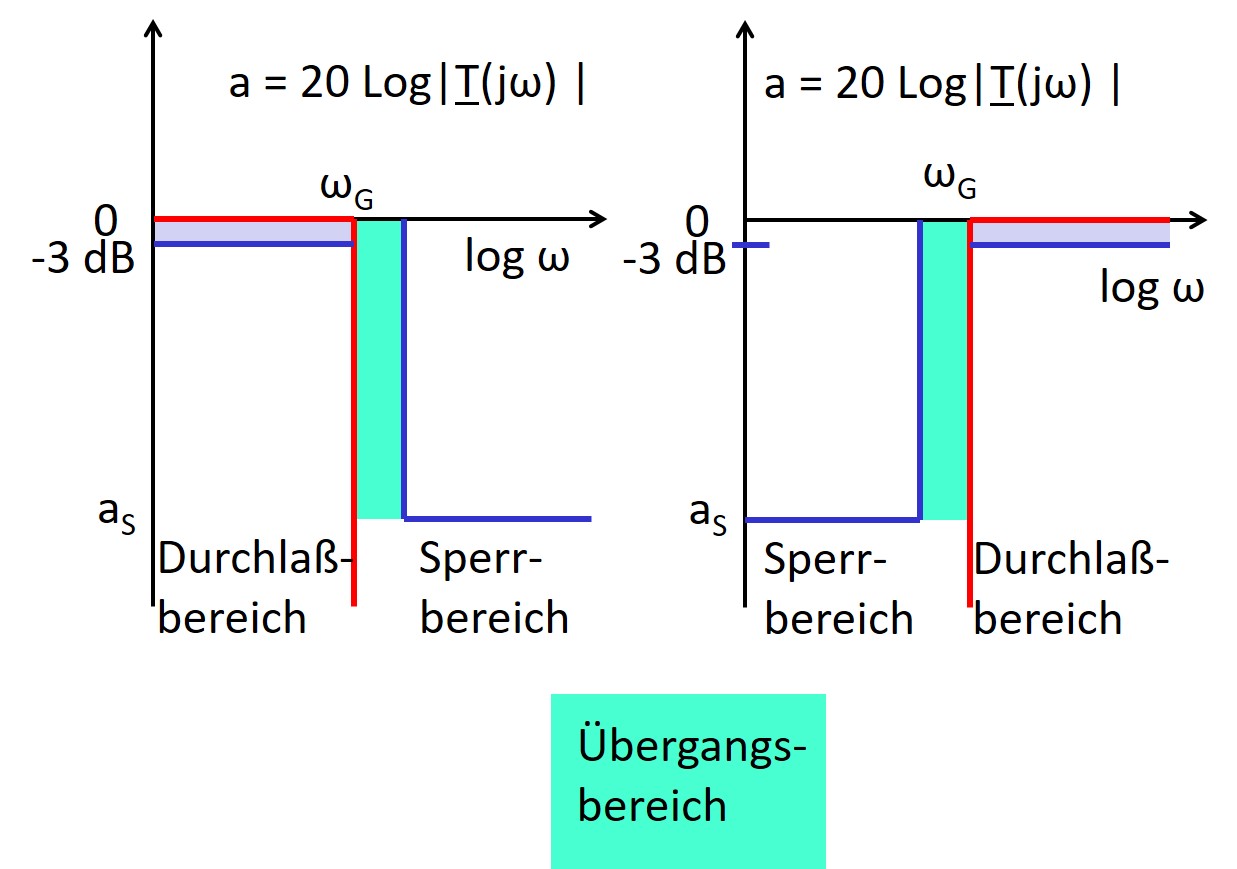
Ordnungszahl n
- Ordnungszahl n
- Grad des Nennerpolynoms n der Übertragungsfunktion (Pol)
- Der Grad des Zählerpolynoms m eines Filters ist immer kleiner
oder gleich dem Grad des Nennerpolynoms
m ≤ n - Der Verlauf von \( \underline{a}_t(\omega) \) und φt(ω) wird von der Ordnungszahl bestimmt, den Polen und Nullstellen, den Koeffizienten.
Tiefpass (Low pass)
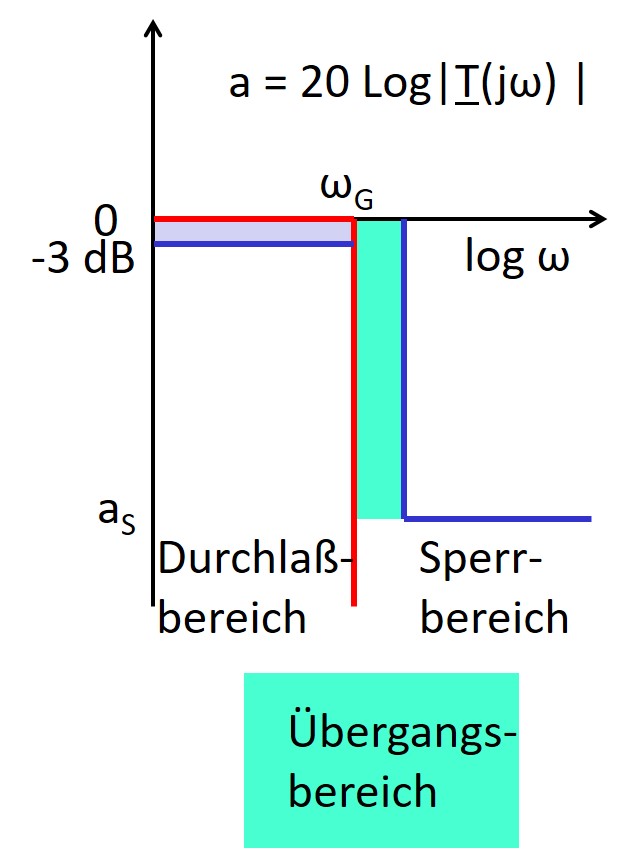
- Idealer Tiefpass (rot)
- Realer Tiefpass
Realer Tiefpass
- ω = 0
t(jω) > 0
keine Nullstelle - Grad des Zählerpolynoms kleiner als Grad des Nennerpolynoms
ω → ∞
t(jω) → 0 - Ein Tiefpass erster Ordnung ist ein elementarer Tiefpass
- Er enthält einen Kapazitiven oder induktiven Grundzweipol
- Man erkennt einen Tiefpass in dem man die Ersatzschaltungen für ω=0 und ω → ∞ bildet.
Realer Tiefpass Schaltung
|
Betrachtung ω = 0 ω → ∞ \( \underline{T}(j\omega) = \frac{\underline{I}_V (j\omega)} {\underline{I}_q (j\omega)} = \) |
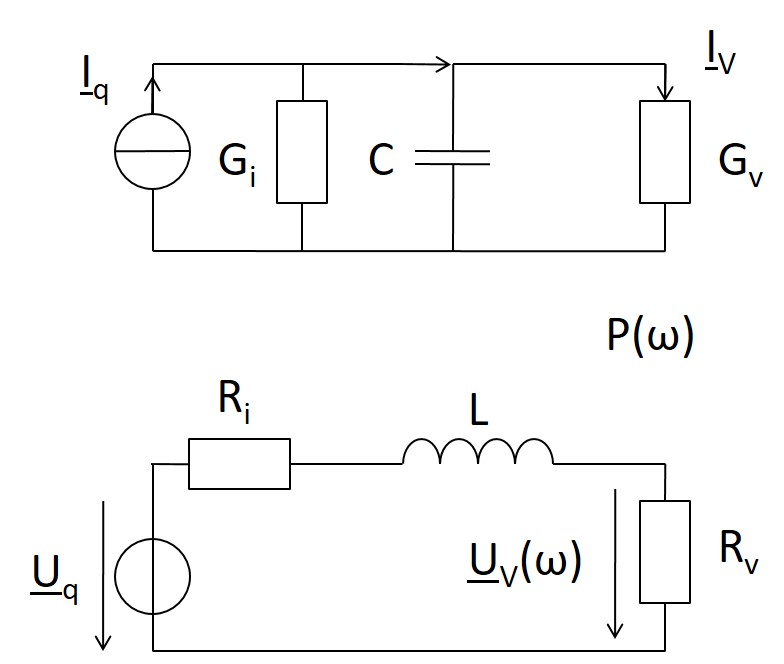 |
\( \underline{T}(j\omega) = \frac{\underline{I}_V (j\omega)} {\underline{I}_q (j\omega)} = = \frac{G_V}{j \omega C + G_i + G_V} = \frac{G_V}{C} \frac{1}{j \omega + \frac{G_i + G_V}{C}} \)
\( \underline{T}(j\omega) = \frac{\underline{U}_V (j\omega)} {\underline{U}_q (j\omega)} = = \frac{R_V}{j \omega L + R_i + R_V} = \frac{R_V}{L} \frac{1}{j \omega + \frac{R_i + R_V}{L}} \)
Die Grenzfrequenz wird vom Quellenwiderstand und Lastwiderstand bestimmt.
Realer Tiefpass Schaltung
Lösung
Normierung
Betrag (Maß) und Phase
Grenzfrequenz
Beispiel Tiefpass
In einem Netz sollen die Frequenzen im Bereich von f = 0 Hz bis f = 5 kHz gut übertragen und die Frequenzen f = f2 = 20 kHz möglichst stark gedämpft werden.
Wir wollen überprüfen, wie diese Forderungen von einem Tiefpass 1. Ordnung erfüllt werden können.
Wie kann man den Tiefpass mit R und C dimensionieren.
\( \omega_g = \frac{1}{R C} \)
\( R C = \frac{1}{ 2 \pi f_g} \)
Größenordnung R und C:
10 Ω < R < 1 MΩ
1 pF < C < 500 µF
R = 10 kΩ
\( C = \frac{1}{2 \pi f_g R} = 3.2 nF \)
\( a_{v2} = 20 log \frac{1}{C R} \frac{1}{\left| j 2 \pi f_2 + \frac{1}{R C}\right|} = -12.3 dB \)
Ein Faktor von 4 entspricht 12 dB.
\( R C = \frac{1}{ 2 \pi f_g} \)
Größenordnung R und C:
10 Ω < R < 1 MΩ
1 pF < C < 500 µF
R = 10 kΩ
\( C = \frac{1}{2 \pi f_g R} = 3.2 nF \)
\( a_{v2} = 20 log \frac{1}{C R} \frac{1}{\left| j 2 \pi f_2 + \frac{1}{R C}\right|} = -12.3 dB \)
Ein Faktor von 4 entspricht 12 dB.
Beispiel Tiefpass LTSPICE
LTSPICESPICE Netlist V1 N001 0 AC 1 0 R1 N002 N001 1k C1 N002 0 300n R2 N002 0 1k .ac dec 5 1 1000000Schaltungsrealisierung  |
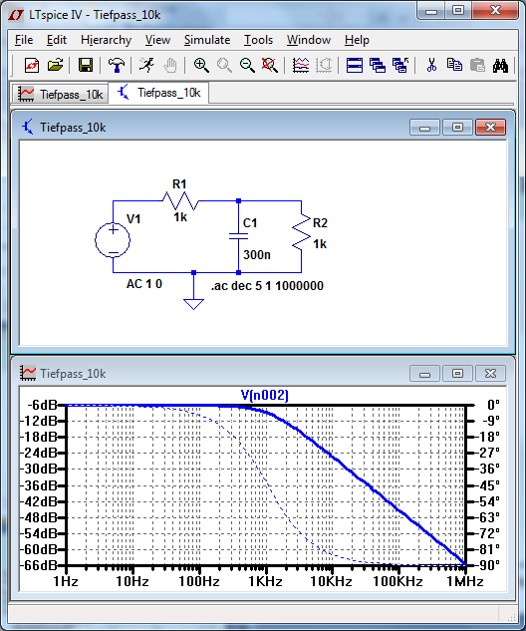 |
Belasteter (R2) Tiefpass ( R1, C1)
Ohmscher Spannungsteiler R1, R2:
\( U_{R2} = U_{1} \frac{R_2}{R_1 + R_2} = U_{1} 0.5 \)
\( a_v = 20 log \frac{U_{R2}}{U_{1}} = -6 dB \)
Übertragungsfunktion:
\( \underline{T} (j\omega) = \frac{\underline{U}_{R_2}}{\underline{U}_{1}} = \frac{\frac{1}{j \omega C_1 + \frac{1}{R_2}}}{R_1 + \frac{1}{j \omega C_1 + \frac{1}{R_2}}} = \frac{1}{R_1 \left( j \omega C_1 + \frac{1}{R_2} \right) + 1} = \frac{1}{ j \omega C_1 R_1 + \frac{R_1}{R_2} + 1} = \frac{1}{C_1 R_1} \frac{1}{ j \omega + \frac{1}{C_1 R_1} \left( 1 + \frac{R_1}{R_2}\right) } \)
Vergleicht man diesen Spannungsteiler mit einem unbelasteten RC-Tiefpass (Es fehlt R2) verschiebt sich die Grenzfrequenz.
Achtung, wenn man einen Spannungsteiler belastet (Spannungsteiler, HP, TP, BP).
Grenzfrequenz:
\( f_{g1} = \frac{1}{2 \pi R_2 C_1} = 7.23 kHz \)
\( f_{g} = \frac{1}{2 \pi C_1} \left( \frac{1}{R_2} + \frac{1}{R_1} \right) = 14.47 kHz \)