Grundlagen Elektrotechnik 2 (GET2)21 Hochpass und TiefpassProf. Dr. Jörg Vollrath20 Filter |

|
Video der 19. Vorlesung 8.6.2021
|
Länge: 1:22:04 |
0:0:0 Evaluierung 0:0:0 Differenzverstärker 0:2:0 Eingangs und Ausgangswiderstand |
Übersicht
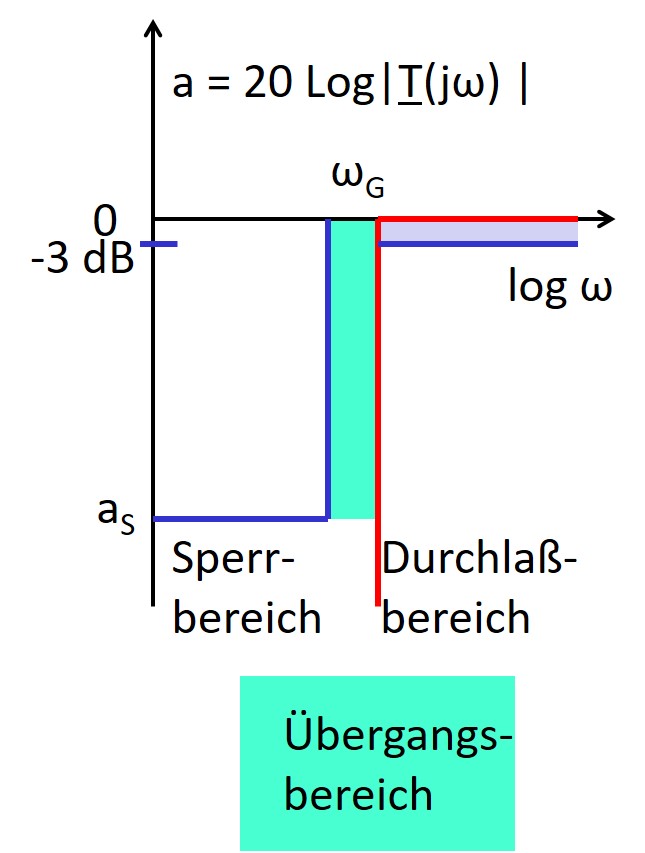
- Filter
- Bandpass, Tiefpass, Hochpass
- Übertragungsfunktion, Pole, Nulstellen
Hochpass (High pass)
Realer Hochpass
- Die Übertragungsfunktion muss eine Nullstelle sN aufweisen
- ω = 0 Signale werden nicht übertragen
- Der Grad von Zählerpolynom und Nennerpolynom muss gleich sein, damit für ω → ∞ der Übertragungsfaktor einen endlichen Wert hat.
- Ein Hochpass erster Ordnung ist ein elementarer Hochpass
- Er enthält einen kapazitiven oder induktiven Grundzweipol.
- Man erkennt einen Hochpass in dem man die Ersatzschaltungen für ω = 0 und ω → ∞ bildet.
Realer Hochpass Schaltbild
Simulation des Frequenzgangs |
Beispiel Hochpass
Wir wollen einen Hochpass erster Ordnung mit einem idealen kapazitiven Zweipol dimensionieren. Seine 3-dB-Grenzfrequenz soll 20 Hz sein. Bei hohen Frequenzen soll die Quelle mit dem Innenwiderstand Ri = 2 kΩ die maximal mögliche Leistung entnommen werden.
Leistungsanpassung: RV = Ri = 2 kΩ
\( C = \frac{1}{\omega_g ( R_i + R_v)} = \)
\( C = \frac{1}{\omega_g ( R_i + R_v)} = \)
Praxisbezug RC-Verstärker
Bei den sog. RC-Verstärkern wird die Wechselspannungsquelle über einen
Kondensator an den Eingang des Verstärkers gekoppelt.
Zu der Wechselspannung wird eine Gleichspannung des Spannungsteilers für den Transistorarbeitspunkt addiert.
Dies bildet einen Hochpass erster Ordnung.
Der Verbraucher wird ebenfalls über einen Kondensator mit dem Verstärkerausgang verbunden.
Das Ausgangssignal soll keinen Gleichanteil haben.
Ein Lautsprecher beötigt keinen Gleichanteil.
Dies ergibt einen weiteren Hochpass erster Ordnung.
Zur Berechnung der Spannung UGS gibt es 3 Werkzeuge:
UGS = UGS1 + UGS2
\( I_{Ki} = U_i \cdot j \omega C_2 \)
\( I_{KVdd} = \frac{VDD}{R_1} \)
\( \underline{U}_{GS} = \frac{\left( \underline{I}_{Ki} + \underline{I}_{KVdd} \right)} {\frac{1}{R_1} + \frac{1}{R_2} + j \omega C_2} \)
Die Spannungsquellen werden in Stromquelle umgewandelt.
Es gibt nur einen Knoten UGS.
\( \left( \frac{1}{R_1} + \frac{1}{R_2} + j \omega C_2 \right) \underline{U}_{GSA} = \underline{I}_{Ki} + \underline{I}_{KVdd} \)
Zu der Wechselspannung wird eine Gleichspannung des Spannungsteilers für den Transistorarbeitspunkt addiert.
Dies bildet einen Hochpass erster Ordnung.
Der Verbraucher wird ebenfalls über einen Kondensator mit dem Verstärkerausgang verbunden.
Das Ausgangssignal soll keinen Gleichanteil haben.
Ein Lautsprecher beötigt keinen Gleichanteil.
Dies ergibt einen weiteren Hochpass erster Ordnung.
Zur Berechnung der Spannung UGS gibt es 3 Werkzeuge:
- Superposition
- Quellenumwandlung
- Knotenpotentialverfahren (Knoten und Maschengleichungen)
Superposition
Jede Quelle wird einzeln betrachtet und das Gesamtergebnis ergibt sich aus Addition der Einzelergebnisse.UGS = UGS1 + UGS2
Quellenumwandlung
Da die Spannungsquellen parallel geschaltet sind werden Sie in Stromquellen umgewandelt, um die Ströme zu addieren.\( I_{Ki} = U_i \cdot j \omega C_2 \)
\( I_{KVdd} = \frac{VDD}{R_1} \)
\( \underline{U}_{GS} = \frac{\left( \underline{I}_{Ki} + \underline{I}_{KVdd} \right)} {\frac{1}{R_1} + \frac{1}{R_2} + j \omega C_2} \)
Knotenpotentialanalyse
Die Spannungsquellen werden in Stromquelle umgewandelt.
Es gibt nur einen Knoten UGS.
\( \left( \frac{1}{R_1} + \frac{1}{R_2} + j \omega C_2 \right) \underline{U}_{GSA} = \underline{I}_{Ki} + \underline{I}_{KVdd} \)
Zusammenfassung und nächstes Mal
- Hochpass und Tiefpass
- Bandpass und Bandsperre