Grundlagen Elektrotechnik 2 (GET2)22 Bandpass und BandsperreProf. Dr. Jörg Vollrath21 Tiefpass und Hochpass |

|
Video GET2 01 Einführung kompakt
Video der 19. Vorlesung 8.6.2021
|
Länge: 1:22:04 |
0:0:0 Evaluierung 0:0:0 Differenzverstärker 0:2:0 Eingangs und Ausgangswiderstand |
Übersicht
- Tiefpass
- Hochpass
- Bandpass
- Bandsperre
Bandpass
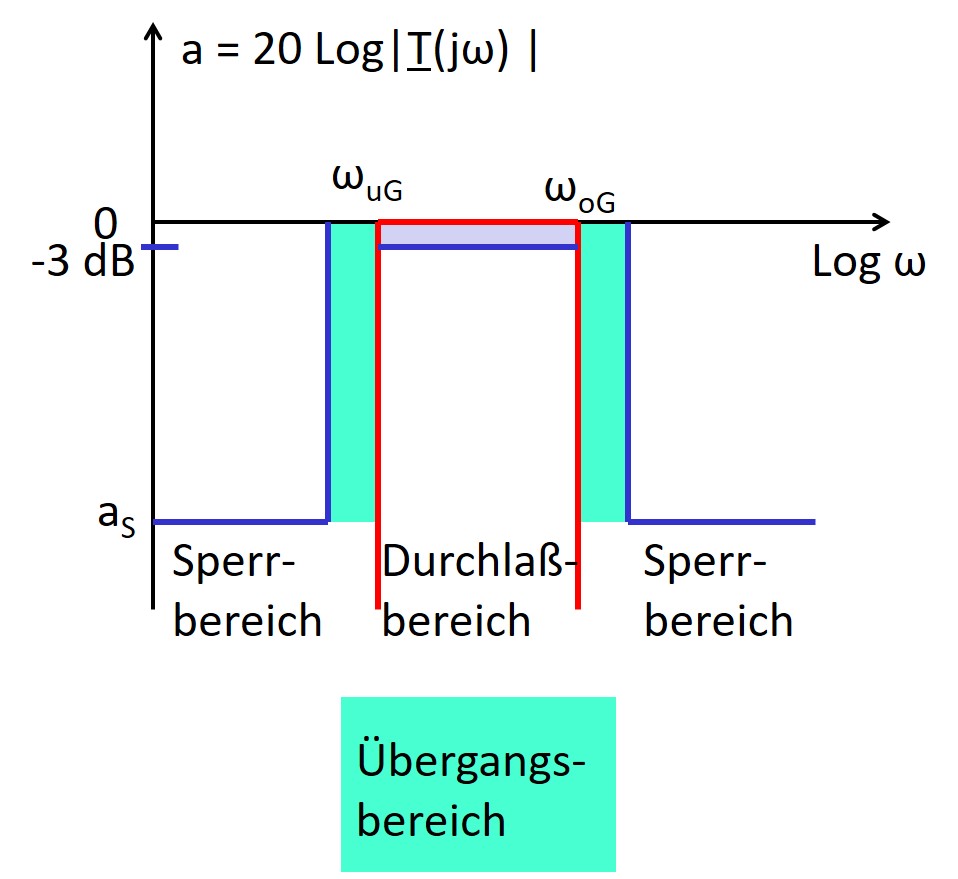
Durchlassbereich zwischen den beiden Grenzfrequenzen Die Differenz wird als Bandbreite (bandwidth) bf bezeichnet. bf = fgo - fgu Manchmal wird auch bω = 2 π bf als Bandbreite bezeichnet |
|
Elementarer Bandpass
|
Übertragungsfunktion Reihenschaltung
\( \underline{T} (j\omega ) = \frac{\underline{U}_V(j\omega)}{\underline{U}_q(j\omega)} = \frac{R_2}{R_1+R_2+ j\omega L +\frac{1}{j\omega C}} = \frac{R_2}{R_1+R_2+ j \left( \omega L - \frac{1}{\omega C} \right)} \)
\( \underline{T} (j\omega ) = \frac{R_2 j\omega C } {(R_1+R_2) j\omega C + (j\omega)^2 L C +1} \)
\( \underline{T} (j\omega ) = \frac{R_2}{L} \frac{j\omega} {(j\omega)^2 + \frac{R_1+R_2}{L} j\omega + \frac{1}{LC}} \)
- Eine Nullstelle: sn0 = 0
- 2 Pole
- Mindestanforderung für einen Bandpass erfüllt
- Resonanz, Schwingkreis
Zur Untersuchung der Schaltung wird die Übertragungsfunktion aufgestellt.
Die Übertragungsfunktion hah Nullstellen (Zähler) und Polstellen (Nenner).
Man hat Potenzen von jω oben und unten stehen.
Die Potenzen sind geordnet und die höchste Potenz hat keinen Vorfaktor.
Für die Polstellen muss man die Nullstellen der quadratischen Gleichung suchen.
Die Übertragungsfunktion hah Nullstellen (Zähler) und Polstellen (Nenner).
Man hat Potenzen von jω oben und unten stehen.
Die Potenzen sind geordnet und die höchste Potenz hat keinen Vorfaktor.
Für die Polstellen muss man die Nullstellen der quadratischen Gleichung suchen.
Übertragungsfunktion Reihenschaltung: Polstellen
\( (j\omega)^2 + \frac{R_1+R_2}{L} j\omega + \frac{1}{LC} = 0 \)
\( (j\omega)_{1,2} = - \frac{R_1+R_2}{2 L} \pm \sqrt{ \left( \frac{R_1+R_2}{2 L} \right)^2 - \frac{1}{LC}} \)
Beispielwerte und Darstellung:
| L / mH | C / uF | R1 / Ω | R2 / Ω | \( \frac{R_1 + R_2}{2 L} \) / s-1 | \( \frac{1}{\sqrt{C L}} \) / s-2 | \( \sqrt{ \left( \frac{R_1+R_2}{2 L} \right)^2 - \frac{1}{LC}} \) / s-2 |
| 2.2 | 72 | 25 | 25 | 11364 | 2513 | 11082 |
| 220 | 0.72 | 25 | 25 | 113.64 | 2513 | j2510 |
| 220 | 0.72 | 125 | 125 | 340.9 | 2513 | j2489 |
Es kann eine oder zwei reelle Lösungen oder komplexe Lösungen geben.
Wie sieht die Übertragungsfunktion für komplexe Lösungen aus?
Wie sieht die Übertragungsfunktion für komplexe Lösungen aus?
Grafische Übertragungsfunktion Reihenschaltung
\( \underline{T} (j\omega ) = \frac{R_2}{L} \frac{j\omega} {(j\omega)^2 + \frac{R_1+R_2}{L} j\omega + \frac{1}{LC}} = \frac{R_2}{L} \frac{j\omega} {(j\omega - \omega_1) (j\omega - \omega_2) } \)
\( a(ω) = 20 * log |\underline{T} (j\omega )| = 20 * log \frac{R_2}{L} + 20 * log \omega - 20 log ( \sqrt{ \left( \frac{1}{LC} - \omega^2 \right)^2 + \left( \frac{R_1+R_2}{L} \omega \right)^2}) \)
Excel: Bandpass
LTSPICE:
Aus welchen Teilfunktionen ergibt sich die Übertragungsfunktion?
Man sieht wie sich die Gesamtfunktion aus den Teilfunktionen zusammen setzt.
Wenn der Imaginärteil des komplexen Widerstandes Null wird, tritt Resonanz auf.
Eine Spannungsüberhöhung kann an L und C auftreten.
Im Übergangsbereich kann sich die Übertragungsfunktion mit mehr als 20 dB/Dekade ändern.
Breitbandig, Schmalbandig, Mittenfrequenz
- Ein Netz kann
- Breitbandig
- gleiche Größenordnung bf, fgo, fgu
- Beispiel: bf=1Mhz, fgo=2Mhz, fgu=1Mhz
- oder Schmalbandig
- Grenzfrequenz wesentlich größer als Bandbreite: bf < fgo, fgu
- Beispiel: bf=1Mhz, fgo=10Mhz, fgu=9Mhz
- Bandmittenfrequenz fm
- Geometrisches Mittel
- \( f_m = \sqrt{f_{go} f_{gu} } \)
- Relative Bandbreite
- \( d = \frac{b_f}{f_m} = \frac{b_\omega}{\omega_m} \)
Charakteristische Gleichung
Reihenschwingkreis Polstellen:
\( (j\omega)^2 + \frac{R_1+R_2}{L} j\omega + \frac{1}{LC} = 0 \)
- 2 unterschiedliche Lösungen
\( (j\omega)_{1,2} = - \frac{R_1+R_2}{2 L} \pm \sqrt{ \left( \frac{R_1+R_2}{2 L} \right)^2 - \frac{1}{LC}} \) - Eine reelle Doppellösung
\( (j\omega)_{1,2} = - \frac{R_1+R_2}{2 L} \) - Zwei konjugiert komplexe Lösungen
\( (j\omega)_{1,2} = - \frac{R_1+R_2}{2 L} \pm j \sqrt{ \left( \frac{1}{LC} - \frac{R_1+R_2}{2 L} \right)^2} \)
Bandbreite
Bestimmung der 3 dB Eckfrequenzen
\( \underline{T} (j\omega ) = \frac{\underline{U}_V(j\omega)}{\underline{U}_q(j\omega)} = \frac{R_2}{R_1+R_2+ j \left( \omega L - \frac{1}{\omega C} \right)} \)
\( R_1+R_2+ j \left( \omega L - \frac{1}{\omega C} \right) = R \cdot (1 \pm j) \)
\( \omega L - \frac{1}{\omega C} = \pm R \)
\( \omega^2 \pm \omega \frac{R_1 + R_2}{ L} - \frac{1}{L C} = 0 \)
\( \omega = \pm \frac{R_1 + R_2}{ 2 L} \pm \sqrt{ \left( \frac{R_1 + R_2}{ 2 L} \right)^2 + \frac{1}{L C}} \)
4 Lösungen, 2 kleiner Null.
Bandbreite Lösung
\( \omega = \pm \frac{R_1 + R_2}{ 2 L} \pm \sqrt{ \left( \frac{R_1 + R_2}{ 2 L} \right)^2 + \frac{1}{L C}} \)
4 Lösungen, 2 kleiner Null.
\( \omega_{go} = \frac{R_1 + R_2}{ 2 L} + \sqrt{ \left( \frac{R_1 + R_2}{ 2 L} \right)^2 + \frac{1}{L C}} \)
\( \omega_{gu} = - \frac{R_1 + R_2}{ 2 L} + \sqrt{ \left( \frac{R_1 + R_2}{ 2 L} \right)^2 + \frac{1}{L C}} \)
\( \omega_{go} - \omega_{gu} = \frac{R_1 + R_2}{ 2 L} + \sqrt{ \left( \frac{R_1 + R_2}{ 2 L} \right)^2 + \frac{1}{L C}} - \left( - \frac{R_1 + R_2}{ 2 L} + \sqrt{ \left( \frac{R_1 + R_2}{ 2 L} \right)^2 + \frac{1}{L C}} \right)\)
\( \omega_{go} - \omega_{gu} = 2 \frac{R_1 + R_2}{ 2 L} = \frac{R_1 + R_2}{ L} \)
Mittenfrequenz Lösung
\( \omega_{go} = \frac{R_1 + R_2}{ 2 L} + \sqrt{ \left( \frac{R_1 + R_2}{ 2 L} \right)^2 + \frac{1}{L C}} \)
\( \omega_{gu} = - \frac{R_1 + R_2}{ 2 L} + \sqrt{ \left( \frac{R_1 + R_2}{ 2 L} \right)^2 + \frac{1}{L C}} \)
\( \omega_{go} \cdot \omega_{gu} = \left( \frac{R_1 + R_2}{ 2 L} + \sqrt{ \left( \frac{R_1 + R_2}{ 2 L} \right)^2 + \frac{1}{L C}} \right) \cdot \left( - \frac{R_1 + R_2}{ 2 L} + \sqrt{ \left( \frac{R_1 + R_2}{ 2 L} \right)^2 + \frac{1}{L C}} \right) \)
\( \omega_{go} \cdot \omega_{gu} = \left( \frac{R_1 + R_2}{ 2 L} \right)^2 + \frac{1}{ L C} - \left( \frac{R_1 + R_2}{ 2L} \right)^2 = \frac{1}{ L C} = \omega_r^2 \)
\( \omega_r^2 = \omega_{go} \cdot \omega_{gu} = \frac{1}{ L C} \)
Güte
Güte Q ist das Verhältnis von Resonanzfrequenz, Mittenfrequenz und Bandbreite
\( Q = \frac{\omega_r}{b_{\omega}} = \frac{\omega_r}{\omega_o - \omega_u} = \frac{1}{R}\sqrt{\frac{L}{C}} \)
Je kleiner die Bandbreite, desto größer die Güte.
Die Güte ist Einheitslos
Beispielwerte Reihenschwingkreis
| L / mH | C / uF | R1 / Ω | R2 / Ω |
| 2.2 | 72 | 25 | 25 |
| 220 | 0.72 | 25 | 25 |
| 220 | 0.72 | 125 | 125 |
Bandbreite: \( b_{\omega} = \frac{R_2}{ L} \)
Mittenfrequenz: \( \omega_m = \frac{1}{ \sqrt{L C}} \)
Relative Bandbreite: \( d = R_2 \sqrt{\frac{C}{L}} \)
Güte: \( Q = \frac{1}{R_2} \sqrt{\frac{L}{C}} \)
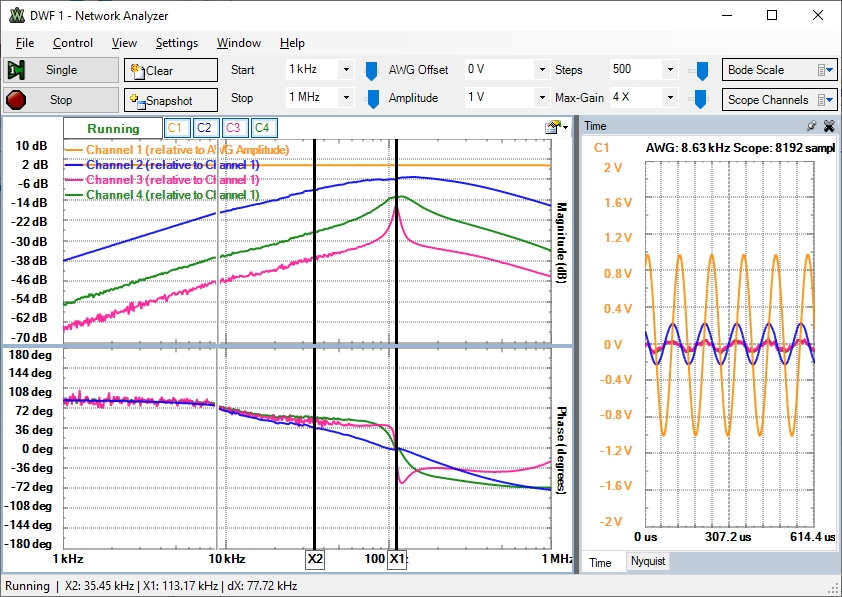
Electroni Explorer:

Mittenfrequenz: \( \omega_m = \frac{1}{ \sqrt{L C}} \)
Relative Bandbreite: \( d = R_2 \sqrt{\frac{C}{L}} \)
Güte: \( Q = \frac{1}{R_2} \sqrt{\frac{L}{C}} \)
Electroni Explorer:
| L / uH | C / nF | R2 / Ω |
| 22 | 100 | 20 |
| 220 | 10 | 20 |
| 2200 | 1 | 20 |


Bandsperre und Bandpass
Rx = 2.5 kΩ
Man sieht wie nach Umwandlung der LC Parallelschaltung in eine Reihenschaltung aus dem Bandpass eine Bandsperre wird.
Die Schaltungen rechts mit nur einem L oder C dienen der Veranschaulichung, wie sich die Übertragungsfunktion aus Teilfunktionen zusammen setzt.
Man sieht wie nach Umwandlung der LC Parallelschaltung in eine Reihenschaltung aus dem Bandpass eine Bandsperre wird.
Die Schaltungen rechts mit nur einem L oder C dienen der Veranschaulichung, wie sich die Übertragungsfunktion aus Teilfunktionen zusammen setzt.
Bandsperre
\( \frac{\underline{U}_a}{\underline{U}_i}
= \frac{R_2}{R_1 + R_2 + \frac{1}{j \omega C_1 + \frac{1}{j \omega L_1}}} \)
\( \frac{\underline{U}_a}{\underline{U}_i} = \frac{R_2}{R_1 + R_2 + \frac{j \omega L_1}{(j \omega)^2 C_1 L_1 + 1}} \)
\( \frac{\underline{U}_a}{\underline{U}_i} = \frac{R_2 \left( (j \omega)^2 C_1 L_1 + 1 \right)} {\left( R_1 + R_2 \right) \left( (j \omega)^2 C_1 L_1 + 1 \right) + j \omega L_1} \)
\( \frac{\underline{U}_a}{\underline{U}_i} = \frac{R_2}{R_1 + R_2} \frac{(j \omega)^2 + \frac{1}{C_1 L_1}} { (j \omega)^2 + j \omega \frac{1}{C_1 \left( R_1 + R_2 \right)} + \frac{1}{C_1 L_1} } \)
\( K = \frac{R_2}{R_1 + R_2} \)
\( S_{N1,2} = \pm j \frac{1}{\sqrt{C_1 L_1}}\)
\( S_{P1,2} = - \frac{1}{2 C_1 \left(R_1 +R_2\right)} \pm \sqrt{\frac{1}{4 C_1^2 \left(R_1 +R_2\right)^2} - \frac{1}{C_1 L_1}} \)
\( Q = R \sqrt{\frac{C_1}{L_1}} \)
\( \frac{\underline{U}_a}{\underline{U}_i} = \frac{R_2}{R_1 + R_2 + \frac{j \omega L_1}{(j \omega)^2 C_1 L_1 + 1}} \)
\( \frac{\underline{U}_a}{\underline{U}_i} = \frac{R_2 \left( (j \omega)^2 C_1 L_1 + 1 \right)} {\left( R_1 + R_2 \right) \left( (j \omega)^2 C_1 L_1 + 1 \right) + j \omega L_1} \)
\( \frac{\underline{U}_a}{\underline{U}_i} = \frac{R_2}{R_1 + R_2} \frac{(j \omega)^2 + \frac{1}{C_1 L_1}} { (j \omega)^2 + j \omega \frac{1}{C_1 \left( R_1 + R_2 \right)} + \frac{1}{C_1 L_1} } \)
\( K = \frac{R_2}{R_1 + R_2} \)
\( S_{N1,2} = \pm j \frac{1}{\sqrt{C_1 L_1}}\)
\( S_{P1,2} = - \frac{1}{2 C_1 \left(R_1 +R_2\right)} \pm \sqrt{\frac{1}{4 C_1^2 \left(R_1 +R_2\right)^2} - \frac{1}{C_1 L_1}} \)
\( Q = R \sqrt{\frac{C_1}{L_1}} \)
Tiefpass 2ter Ordnung
Bestimmen Sie die Übertragungsfunktion.
Active Filter
Texas instruments: OpAmps for everyone
Ch-16 Active Filter Design Techniques
Sallen-Key Topology
Knotenspannung Vx
Stromgleichungen, Knotengleichungen
(1) \( \frac{V_{in}-V_{x}}{R_1} = \frac{V_x-V_{out}}{R_2} + (V_x-V_{out}) j \omega C_2 \)
(2) \( \frac{V_x-V_{out}}{R_2} = V_{out} j \omega C_1 \)
(2') \( V_x = V_{out} (j \omega C_1 R_2 + 1) \)
(2),(2') in (1)
\( \frac{V_{in}}{R_1} - V_{out} \frac{(j \omega C_1 R_2 +1)}{R_1} = V_{out} j \omega C_1 + V_{out} R_2 j \omega C_1 j \omega C_2 \)
\( \frac{V_{in}}{R_1} = V_{out} ( j \omega C_1 + (j \omega )^{2} C_1 C_2 R_2 + \frac{1}{R_1} + j \omega C_1 \frac{R_2}{R_1} \)
\( \frac{V_{out}}{V_{in}} = \frac{1} {j \omega C_1 R_1 + (j \omega)^2 C_1 C_2 R_2 R_1 + 1 + j \omega C_1 R_2} \)
\( \frac{V_{out}}{V_{in}} = \frac{1}{1 + j \omega C_1 (R_1 + R_2) + (j\omega)^2 C_1 C_2 R_2 R_1} \)
Koeffizienten: Bessel, Butterworth, Tschebyscheff
Stellen Sie die Gleichung für die Übertragungsfunktion auf.
Reference: TI, Op amp for everyone
Knotenspannung Vx
Stromgleichungen, Knotengleichungen
(1) \( \frac{V_{in}-V_{x}}{R_1} = \frac{V_x-V_{out}}{R_2} + (V_x-V_{out}) j \omega C_2 \)
(2) \( \frac{V_x-V_{out}}{R_2} = V_{out} j \omega C_1 \)
(2') \( V_x = V_{out} (j \omega C_1 R_2 + 1) \)
(2),(2') in (1)
\( \frac{V_{in}}{R_1} - V_{out} \frac{(j \omega C_1 R_2 +1)}{R_1} = V_{out} j \omega C_1 + V_{out} R_2 j \omega C_1 j \omega C_2 \)
\( \frac{V_{in}}{R_1} = V_{out} ( j \omega C_1 + (j \omega )^{2} C_1 C_2 R_2 + \frac{1}{R_1} + j \omega C_1 \frac{R_2}{R_1} \)
\( \frac{V_{out}}{V_{in}} = \frac{1} {j \omega C_1 R_1 + (j \omega)^2 C_1 C_2 R_2 R_1 + 1 + j \omega C_1 R_2} \)
\( \frac{V_{out}}{V_{in}} = \frac{1}{1 + j \omega C_1 (R_1 + R_2) + (j\omega)^2 C_1 C_2 R_2 R_1} \)
Koeffizienten: Bessel, Butterworth, Tschebyscheff
Multiple Feedback Topology
Stellen Sie die Gleichung für die Übertragungsfunktion auf.
Reference: TI, Op amp for everyone
Polynomfilter (Digital Signal Processing)
\( \underline{T}(j \omega) = K \frac{1}{(j\omega)^n + b_1 (j\omega)^{n-1} +...+ b_n}\)
- Tabellen
- Butterworth Filter
- Tschebyschew Filter
- Bessel Filter
- Digitalfilter
RC-Tiefpass-Filter
Übertragungsfunktion
\( \underline{T}(j\omega) = \frac{1}{j\omega R C + 1}\)
Differentialgleichung
\( C = \frac{I dt}{dU} \)
\( dU = \frac{I dt}{C} \)
\( U_{out} (t+dt) = U_{out} (t) + \frac{I dt}{C} = U_{out} (t) + \frac{U_{in} (t) - U_{out}(t) dt}{R C} = (1 - k_2) \cdot U_{out} (t) + k_2 \cdot U_{in} (t) \)
\( U_{out} (t) = k_1 \cdot U_{out} (t-dt) + k_2 \cdot U_{in} (t-dt) \)
dt: TCLK
Übertragungsfunktion
\( \underline{T}(j\omega) = \frac{1}{j\omega R C + 1}\)
Differentialgleichung
\( C = \frac{I dt}{dU} \)
\( dU = \frac{I dt}{C} \)
\( U_{out} (t+dt) = U_{out} (t) + \frac{I dt}{C} = U_{out} (t) + \frac{U_{in} (t) - U_{out}(t) dt}{R C} = (1 - k_2) \cdot U_{out} (t) + k_2 \cdot U_{in} (t) \)
\( U_{out} (t) = k_1 \cdot U_{out} (t-dt) + k_2 \cdot U_{in} (t-dt) \)
dt: TCLK
Zusammenfassung und nächstes Mal
- Bandpass
- Obere und untere Eckfrequenz, Bandbreite
- Mittenfrequenz
- Güte
25 Drehstrom