Grundlagen Elektrotechnik 2 (GET2)23 TransformatorProf. Dr. Jörg Vollrath19 Vierpol 22 Bandpass und Bandsperre |

|
Video GET2 01 Einführung kompakt
Video der 19. Vorlesung 8.6.2021
|
Länge: 1:22:04 |
0:0:0 Evaluierung 0:0:0 Differenzverstärker 0:2:0 Eingangs und Ausgangswiderstand |
Übersicht
- Bandsperre, Bandpass
- Evaluierung
- Review Ortskurventest
- Springer Bücher
Bibliothek
Grundlagen der Elektrotechnik und Elektronik
Rückblick Vierpol
- Es gibt verschiedene Matrizen:
- Widerstandsmatrix, Leitwertmatrix, Kettenmatrix
- Die Koeffizienten können durch Messung oder Rechnung bestimmt werden.
- Bei der Messung wird bei Kurzschluss oder Leerlauf eines Klemmenpaars, alle Ströme und Spannungen gemessen.
- Die Kettenmatrix einer Kettenschaltung von Vierpolen entsteht durch die Multiplikation der einzelnen Matrizen.
- Die Reihenfolge ist entscheidend.
Transformator als Vierpol: Inhalt
- Idealer Transformator
- Beispiele: Netztransformator, NF, HF Transformator
- Idealer Transformator
- Übersetzungsverhältnis: ü
- Impedanzwandler
- Leistungsbilanz
- Gegeninduktivität M
- Realer Transformator
- Kopplungsfaktor
- Streufaktor
- Ersatzschaltbilder
- Beispiele
Ziele
- Die Eigenschaften des idealen und realen Transformators kennenlernen
- Das Spannungs- und Stromübersetzungsverhältnis und die Impedanzwandlung kennen
- Ersatzschaltbilder entwickeln können
- Die Messung der Elemente des Ersatzschaltbildes eines Transformators
- Die Dimensionierung eines Transformators verstehen.
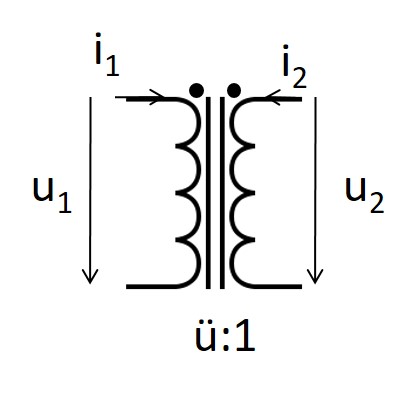
Idealer Transformator
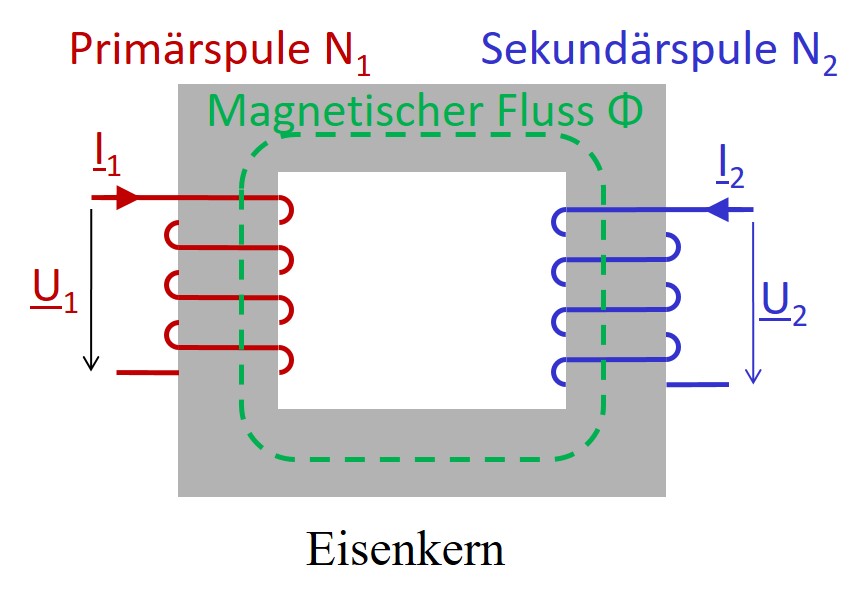 \( \frac{u_1}{u_2} = \frac{N_1}{N_2} = ü \) \( \frac{i_1}{i_2} = - \frac{N_2}{N_1} = - \frac{1}{ü} \) \( u_2 \cdot i_2 = u_1 \cdot i_1 \) |
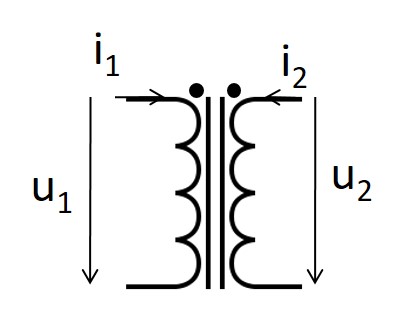 Punkte: Wicklungsrichtung Gleichsinnige Wicklung Galvanische Trennung Potenzialtrennung Verbraucherzählpfeilsystem |
Elektrische Schaltbilder
 Mit Kern |
 Mit Luftspalt im Kern |
 Lufttransformator | |
 Gleichsinnige Wicklung | Verbraucher Pfeilsystem |
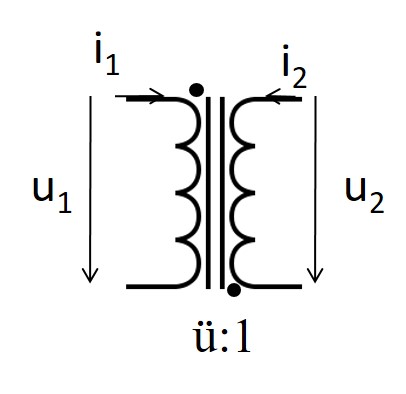 Gegensinnige Wicklung |
Transformatoren: Leistungstransformator Signalübertrager



Steckernetzteil (rechts 3.6W)
Schaltnetzteil (links, 20W)
Signalübertrager Ethernet TG110
Schaltnetzteil (links, 20W)
Signalübertrager Ethernet TG110
Idealer Transformator
|
  |
Übersetzungsverhältnis
|
Verbraucher- Zählpfeilsystem | 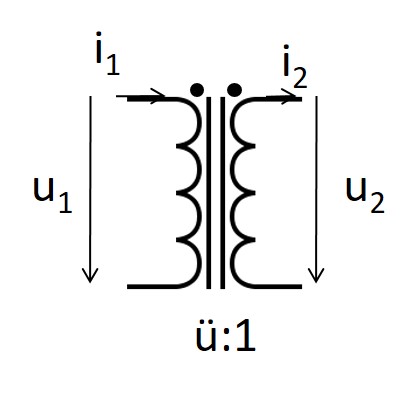
| Erzeuger- Zählpfeilsystem |
\( \frac{u_1}{u_2} = \frac{i_2}{i_1} = \frac{N_1}{N_2} = ü \)
Komplexe Schreibweise
\( \frac{\underline{U}_1}{\underline{U}_2} = \frac{\underline{I}_2}{\underline{I}_1} = \frac{N_1}{N_2} = ü \)
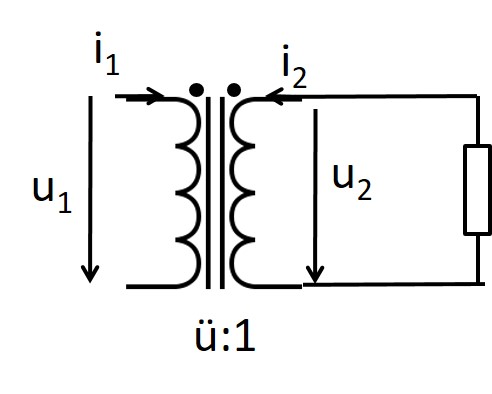
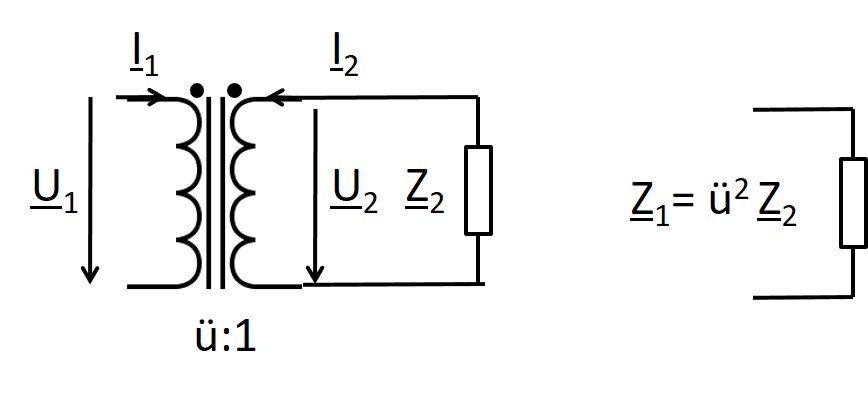
Eingangswiderstand: Impedanzwandler
|
\( R_1 = \frac{u_1}{i_1} = \frac{ü u_2}{-\frac{i_2}{ü}} \) \( R_1 = ü^2 \frac{- u_2}{i_2} = ü^2 R_2 \) Impedanzwandler Komplexe Rechnung \( \underline{Z}_1 = ü^2 \underline{Z}_2 \) |
  |
Leistungsbilanz
p1= u1 i1 = p2= u2 i2
Der ideale Transformator speichert keine Energie!
Schein-, Wirk- und Blindleistung sind beim idealen Transformator auf Primär- und Sekundärseite gleich (invariant)
S1= U1 I1 = S2 = U2 I2
\( \underline{S}_1= \underline{U}_1 \underline{I}_1^* = \underline{S}_2 = \underline{U}_2 \underline{I}_2^* \)
\( P_1 = Re\{\underline{S}_1\} = P2= Re\{\underline{S}_2\} \)
\( Q_1 = Im\{\underline{S}_1\} = Q_2 = Im\{ \underline{S}_2 \} \)
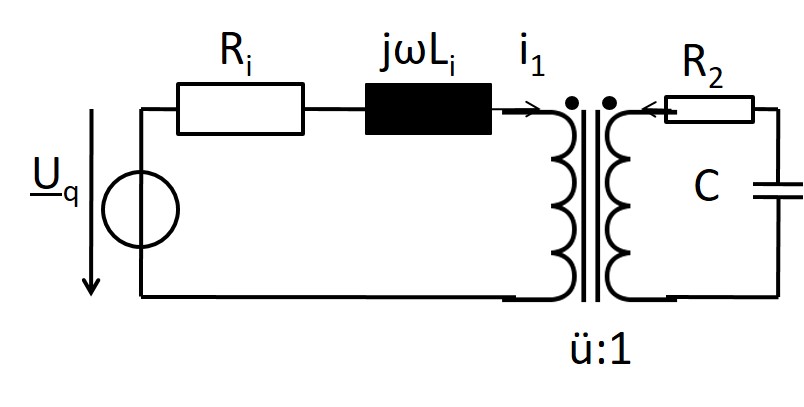
Beispiel: Anpassungsübertrager
|
Spannungsquelle: \( \underline{Z}_i = R_i + j \omega L_i \) Verbraucher R2 = 400 Ω Möglichst große Leistung aufnehmen Gesucht: ü=?, C=?
Maximale Leistung: \( \underline{Z}_i = ü^2 \underline{Z}_a^* \)
\( R_i = ü^2 R_2 \) \( ü = \sqrt{\frac{R_i}{R_2}} \) XL = - ü2 X C \( \omega; L_i = \frac{ü^2}{\omega C} \) \( C = \frac{ü^2}{\omega^2 L_i} \) |
 |
Verlust und streuungsfreier Transformator
Fluß der Wicklung 1 und Fluß der Wicklung 2
Φ1 = Φ2 =Φ = Φ11 + Φ12 = Φ21 + Φ22
Φ11 Fluß in der Wicklung 1 von i1
Φ12 Fluß in der Wicklung 1 von i2
Definition der Induktivität
N φ = L i
Ergebnis: L1, l2 Selbstinduktivität, M Gegeninduktivität
\( \frac{L_1}{N_1} i_1 + \frac{M}{N_1} i_2 = \frac{M}{N_2} i_1 + \frac{L_2}{N_2} i_2 \)
|
Koeffizienten für alle i1,i2 gleich \( \frac{L_1}{N_1} = \frac{M}{N_2} \) → \( M = \frac{N_2}{N_1} L_1 \) \( \frac{L_2}{N_2} = \frac{M}{N_1} \) → \( M = \frac{N_1}{N_2} L_2 \) \( \frac{L_1}{L_2} = \frac{N_1^2}{N_2^2} = ü^2 \)
|
 |
Kopplungs- und Streufaktor
Kopplungsfaktor
|
\( k = \frac{M}{\sqrt{L_1 L_2}} \) |
k=1 Idealfall totaler Kopplung, fehlende Streuung
Sonst: 0 < k < 1
Streufaktor
|
\( \rho = 1 - k^2 = 1 -\frac{M^2}{L_1 L_2} \) |
Induktivität
Induktivität einer Spule auf einem Transformatorenkern
\( L_1 = \frac{ \mu_r \cdot \mu_0 \cdot A_E \cdot N_1^2}{l_e} \)
µr, µ0: relative und absolute Permeabilität
AE: Fläche des Transformatorenkerns
N1: Anzahl der Wicklungen
lE: mittlere Weglänge im Transformatorenkern
\( L_{21} = M = \frac{ \mu_r \cdot \mu_0 \cdot A_E \cdot N_1 \cdot N_2}{l_e} \)
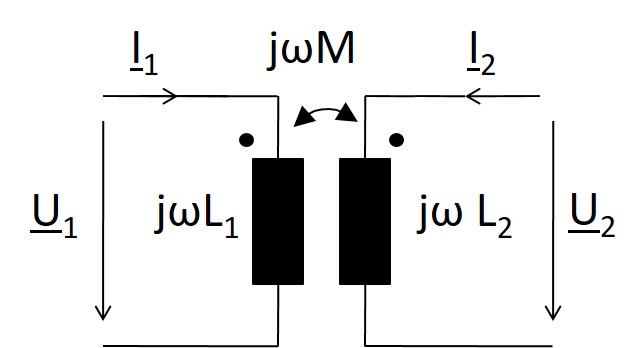
Idealer Transformator:Ersatzschaltbild
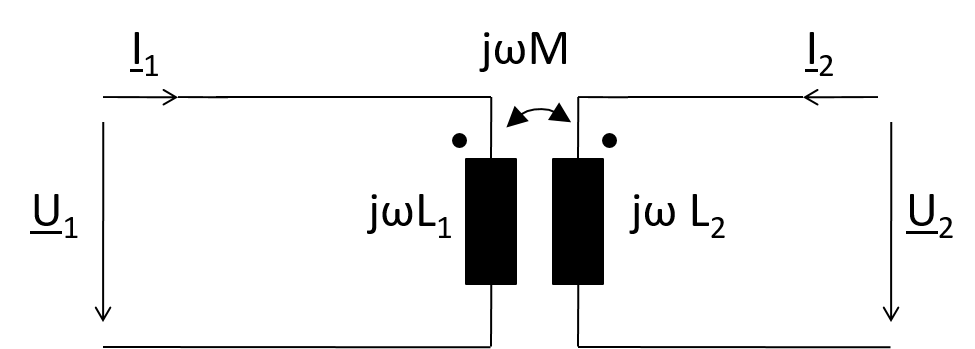
\( u_1(t) = L_1 \cdot \frac{d i_1}{dt} + M \cdot \frac{d i_2}{dt} \)
\( u_2(t) = M \cdot \frac{d i_1}{dt} + L_2 \cdot \frac{d i_2}{dt} \)
Für sinusförmige Größen ergibt sich im komplexen:
\( \underline{U}_1 ( \omega ) = j \omega L_1 \cdot \underline{I}_1 + j \omega M \cdot \underline{I}_2 \)
\( \underline{U}_2 ( \omega ) = j \omega M \cdot \underline{I}_1 + j \omega L_2 \cdot \underline{I}_2 \)
Teil4.pdf, Universität Stuttgart
Ein Magnetstrom i(t) erzeugt eine Feldstärke H und im Transformatorenkern eine magnetische Flussdichte B und einen Fluss Φ.
Ein Magnetstrom i(t) erzeugt eine Feldstärke H und im Transformatorenkern eine magnetische Flussdichte B und einen Fluss Φ.
Magnetisch gekoppelte Spulen
(1) \( \underline{U}_1 ( \omega ) = j \omega L_1 \cdot \underline{I}_1 + j \omega M \cdot \underline{I}_2 \)
(2)\( \underline{U}_2 ( \omega ) = j \omega M \cdot \underline{I}_1 + j \omega L_2 \cdot \underline{I}_2 \)
Es wird (1) mit \( - j \omega M \underline{I}_1 + j \omega M \underline{I}_1 \) und (2) mit \( - j \omega M \underline{I}_2 + j \omega M \underline{I}_2 \) ergänzt:
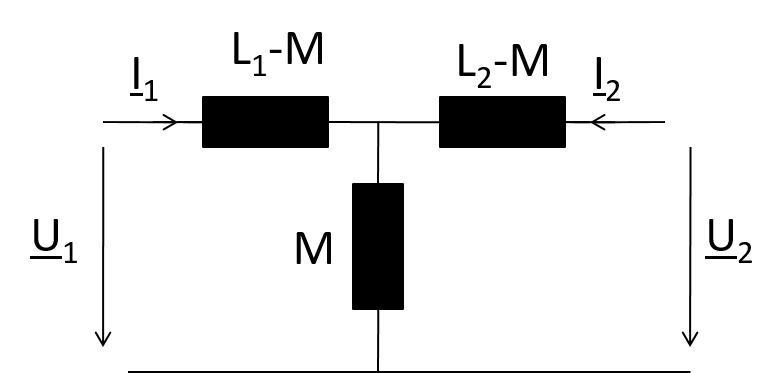
(3) \( \underline{U}_1 ( \omega ) = j \omega (L_1 - M) \cdot \underline{I}_1 + j \omega M \cdot (\underline{I}_2 + \underline{I}_1) \)
(4) \( \underline{U}_2 ( \omega ) = j \omega (L_2 - M) \cdot \underline{I}_2 + j \omega M \cdot (\underline{I}_2 + \underline{I}_1) \)
Diese Gleichungen entsprechen dem obigen Ersatzschaltbild.
Bekommt man mit diesem Ersatzschaltbild ein Spannungsverhältnis?
Start mit Gleichung (2):
\( \underline{U}_2 ( \omega ) = j \omega M \cdot \underline{I}_1 + j \omega L_2 \cdot \underline{I}_2 \)
Einsetzen von \( \underline{I}_1 \) aus Gleichung (1) ergibt:
\( \underline{U}_2 ( \omega ) = \frac{M}{L_1} \left( \underline{U}_1 - j \omega M \cdot \underline{I}_2 \right) + j \omega L_2 \cdot \underline{I}_2 \)
\( \underline{U}_2 ( \omega ) = j \omega \cdot \underline{I}_2 \left( L_2 - \frac{M^2}{L_1}\right) + \frac{M}{L_1} \underline{U}_1 \)
mit k=1 und M2 = L1 L2
\( \underline{U}_2 ( \omega ) = j \omega \cdot \underline{I}_2 \left( L_2 - \frac{L_1 L_2}{L_1}\right) + \frac{\sqrt{L_1 L_2}}{L_1} \underline{U}_1 \)
mit \( v = ü = \sqrt{\frac{L_1}{L_2}} \) ergibt sich:
\( \underline{U}_2 = \frac{\underline{U}_1}{ ü } \)
Start mit Gleichung (2):
\( \underline{U}_2 ( \omega ) = j \omega M \cdot \underline{I}_1 + j \omega L_2 \cdot \underline{I}_2 \)
Einsetzen von \( \underline{I}_1 \) aus Gleichung (1) ergibt:
\( \underline{U}_2 ( \omega ) = \frac{M}{L_1} \left( \underline{U}_1 - j \omega M \cdot \underline{I}_2 \right) + j \omega L_2 \cdot \underline{I}_2 \)
\( \underline{U}_2 ( \omega ) = j \omega \cdot \underline{I}_2 \left( L_2 - \frac{M^2}{L_1}\right) + \frac{M}{L_1} \underline{U}_1 \)
mit k=1 und M2 = L1 L2
\( \underline{U}_2 ( \omega ) = j \omega \cdot \underline{I}_2 \left( L_2 - \frac{L_1 L_2}{L_1}\right) + \frac{\sqrt{L_1 L_2}}{L_1} \underline{U}_1 \)
mit \( v = ü = \sqrt{\frac{L_1}{L_2}} \) ergibt sich:
\( \underline{U}_2 = \frac{\underline{U}_1}{ ü } \)
Berechnung: Transformator Ersatzschaltbild
| L1 | mH | 10 | 10 | 10 | 40 | 250 |
| L2 | mH | 10 | 40 | 250 | 10 | 10 |
| \( M = \sqrt{L_1 \cdot L_2} \) | mH | 10 | 20 | 50 | 20 | 50 |
| \( ü = \sqrt{\frac{L_1}{L_2}}\) | 1 | 0.5 | 0.2 | 2 | 5 | |
| L1 - M | mH | 0 | -10 | -40 | 20 | 200 |
| L2 - M | mH | 0 | 20 | 200 | -10 | -40 |
| U1 | V | 10 | 10 | 10 | 10 | 10 |
| U2 | V | 10 | 20 | 50 | 5 | 2 |
Eine negative Induktivität kann man im komplexen als Kapazität darstellen.
Deshalb ergibt sich obiges Ersatzschaltbild.
\( \omega L = \frac{1}{\omega C} \) \( C = \frac{1}{\omega^2 L} = \frac{1}{ 4 \pi^2 f^2 L} \)
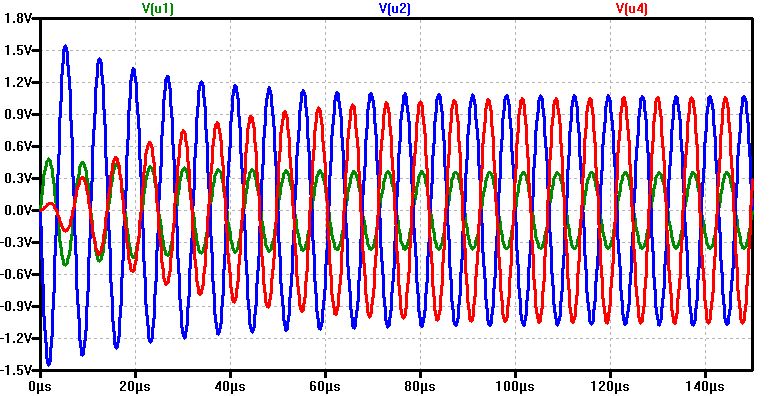
In der Zeitsimulation sieht man bei der gewählten Frequenz von 140kHz, wie aus einer Amplitude u1 = 0.4 V am Ausgang des Transformators und am Ausgang der Ersatzschaltung mit Kondensator und Spule u2 = u4 = 1 V zu beobachten ist.
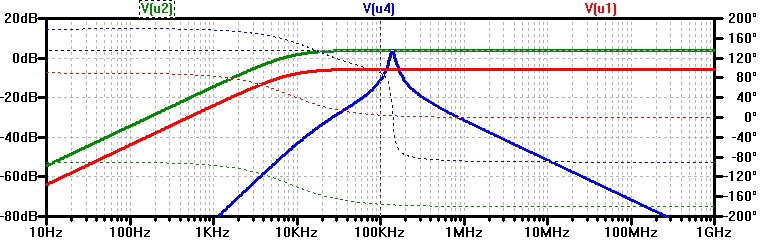
In der AC Simulation sieht man die Resonanz des Ersatzschaltkreises.
Für die gewählte Frequenz von 140kHz verhält sich der CL Schwingkreis wie der Transformator.
Es gibt Resonanz LLC DC-DC Wandler.
\( \omega L = \frac{1}{\omega C} \) \( C = \frac{1}{\omega^2 L} = \frac{1}{ 4 \pi^2 f^2 L} \)

In der Zeitsimulation sieht man bei der gewählten Frequenz von 140kHz, wie aus einer Amplitude u1 = 0.4 V am Ausgang des Transformators und am Ausgang der Ersatzschaltung mit Kondensator und Spule u2 = u4 = 1 V zu beobachten ist.

In der AC Simulation sieht man die Resonanz des Ersatzschaltkreises.
Für die gewählte Frequenz von 140kHz verhält sich der CL Schwingkreis wie der Transformator.
Es gibt Resonanz LLC DC-DC Wandler.
Realer Transformator
T-Ersatzschaltbild
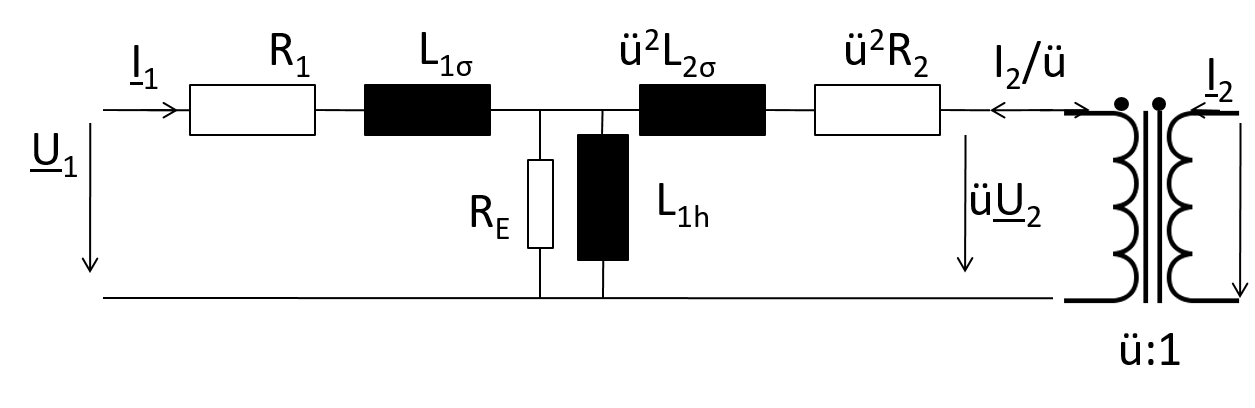
|
 |
Zusammenfassung und nächstes Mal
- Idealer Transformator
\( \frac{U_1}{U_2} = \frac{N_1}{N_2} = ü = \frac{I_2}{I_1}\)
P = U1 · I1 = U2 · I2
Anpassungsübertrager
\( \underline{Z}_1 = ü^2 \underline{Z}_2 \)
Kopplungsfaktor: \( k = \frac{M}{\sqrt{L_1 L_2}} \) Streufaktor - Induktivität
- Realer Transformator
- Wicklungswiderstand, Streuinduktivität, Eisenverluste
