Grundlagen Elektrotechnik 2 (GET2)
24 Transformator
Prof. Dr. Jörg Vollrath
23 Transformator
|
|
|
Video GET2 01 Einführung kompakt
Video der 19. Vorlesung 8.6.2021
Länge: 1:22:04
|
|
Übersicht
- Transformatormessungen
- Leerlaufmessung
- Kurzschlussmessung
- Wirkleistung, Spannung, Strom
- Transformatormodell in LTSPICE
Messung der Ersatzschaltbildgrößen
- Transformatormessungen
- Leerlaufmessung Wirkleistung P, Spannung U, Strom I
\( \underline{S} = \underline{U} \underline{I}^*
= P_{R1} + j Q_{L1}
= R1 \cdot I^2 + j \omega L \cdot I^2\)
\( S = U \cdot I \)
\( Q = \sqrt{ S^2 - P^2} \)
- Kurzschlussmessung: R1, R2, L1, L2
- Gleichspannungsmessung R1 und R2
- Leerlauf Wechselspannungsmessung:
\( \underline{U}_{1L} = (R_1 + j \omega L_1) \underline{I}_1 \)
\( \underline{U}_{2L} = (R_2 + j \omega L_2) \underline{I}_2 \)
- Gegeninduktivität:
- Wechselspannungsmessung Leerlauf:
\( \underline{U}_{2L} = j \omega M \underline{I}_1 \)
- Reihenschaltung und Gegenreihenschaltung
Elektrotechnik für Ingenieure 2, Wilfried Weißgerber, Vieweg und Teubner, Kap 6.4, S. 237ff
Leistungstransformator: Leerlauf
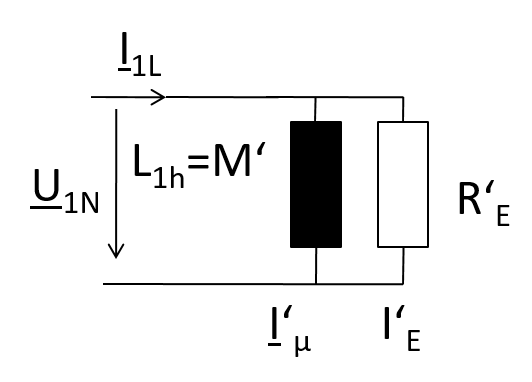
Mit der Leerlaufmessung bestimmt man ü, R'
E und L
1h
\( ü = \frac{U_1}{U_2} \)
Eine Wirkleistungsmessung gibt R'
E:
\( P_{1L} = \frac{U_{1L}^2}{R'_E} \)
\( R'_E = \frac{U_{1L}^2}{P_{1L}} \)
Aus dem Zeigerdiagramm ergibt sich die Hauptinduktivität:
\( X_{L1h} = \omega L_{1h} = \frac{U_{1N}}{I'_{\mu}}
= \frac{U_{1N}}{\sqrt{I_{1L}^{2} - I_{e}^{'2}}}
= \frac{U_{1N}}{\sqrt{I_{1L}^{2} - \left( \frac{U_{1N}}{R'_E}\right)^{2}}} \)
\( \underline{Z}_{L1h} = \frac{1}{\frac{1}{R'_E} + \frac{1}{j \omega L_{1h}}} \)
Scheinleistung: S = U I
Q = S · sin φ = U · I · sin φ
= ω · L · I
2
P = U · I · cos φ
\( \phi = arcsin(\frac{\omega L I^2}{P}) \)
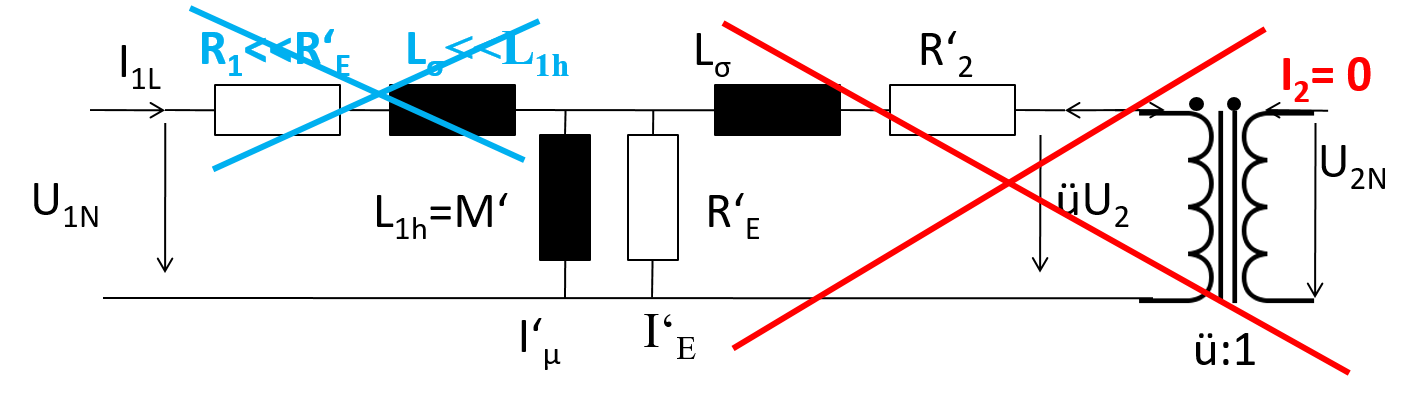
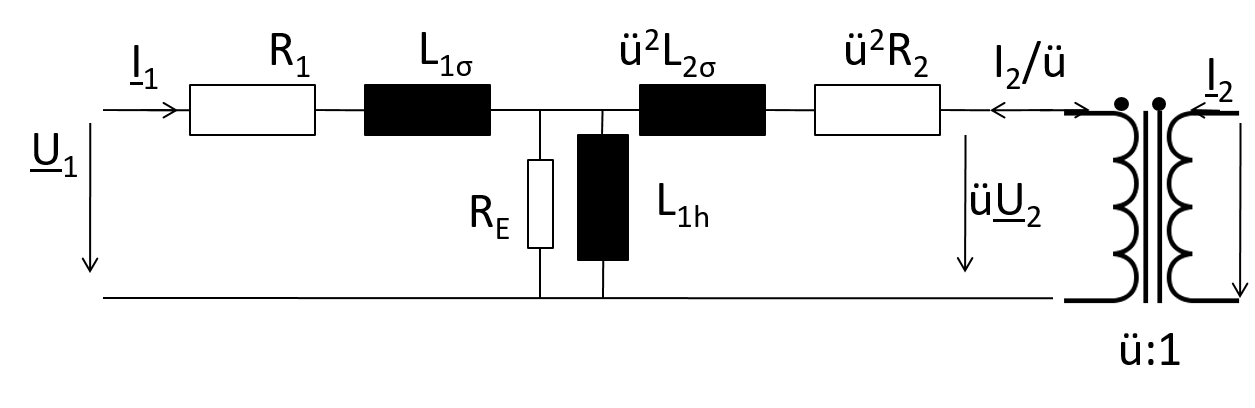
Im Leerlauf fliesst kein Strom, deshalb fallen die rot gekennzeichneten Elemente weg.
Der ohmsche Widerstand der Wicklungen ist viel kleiner als der Eisenwiderstand
und die Streuinduktivität ist viel kleiner als die Hauptinduktivität.
Kurzschluss des Transformators
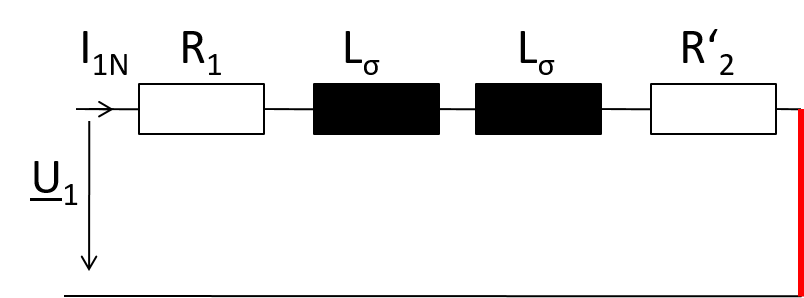
Achtung: Um den Transformator beim Kurzschluss nicht zu überlasten muss die
Eingangsspannung U1 abgesenkt werden.
\( U_1 = \frac{S_N}{I_K} \)
SPICE Transformator
|
|
LTC, Examples, Educational: Transformer
L1 0 N002 100µ
L2 N003 0 900µ
V1 N001 0 PULSE(0 1 0 10n 10n 5u 10u)
R1 N002 N001 10
K1 L1 L2 1
.tran 100u
|
Version 4
SHEET 1 880 680
WIRE -128 176 -288 176
WIRE 0 176 -48 176
WIRE 112 176 0 176
WIRE 368 176 160 176
WIRE -288 192 -288 176
WIRE 112 192 112 176
WIRE 160 192 160 176
WIRE 368 192 368 176
WIRE -288 288 -288 272
WIRE 112 288 112 272
WIRE 160 288 160 272
WIRE 368 304 368 272
FLAG -288 288 0
FLAG 160 288 0
FLAG 112 288 0
FLAG 368 304 0
FLAG 368 176 U2
FLAG 0 176 U1
SYMBOL ind2 128 176 M0
SYMATTR InstName L1
SYMATTR Value 100�
SYMATTR Type ind
SYMBOL ind2 144 288 M180
WINDOW 0 36 80 Left 2
WINDOW 3 36 40 Left 2
SYMATTR InstName L2
SYMATTR Value 900�
SYMATTR Type ind
SYMBOL voltage -288 176 R0
WINDOW 123 24 124 Left 2
WINDOW 39 0 0 Left 2
SYMATTR Value2 AC 1
SYMATTR InstName V1
SYMATTR Value SINE(0 1 100000)
SYMBOL res -32 160 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 10
SYMBOL res 352 176 R0
SYMATTR InstName R2
SYMATTR Value 100
TEXT 80 152 Left 2 !K1 L1 L2 1
TEXT -312 336 Left 2 !;tran 100u
TEXT -392 384 Left 2 ;This example schematic is supplied for informational/educational purposes only.
TEXT -288 104 Left 2 ;A transformer with two windings, 1 to 3 turns winding ratio
TEXT -160 336 Left 2 !.ac dec 10 1 1G
Man sieht den Kopplungsfaktor K1 zwischen L1 und L2
Man sieht die Wicklungen mit Orientierung markiert durch den Kreis.
Man sieht die Induktivitäten L1 und L2.
Bei niedrigen Frequenzen stimmt das Stromübertragungsverhältnis nicht, da es ein Hochpass Verhalten gibt (AC Analyse).
\( ü = 3 = \sqrt{\frac{L_1}{L_2}} \)
SPICE Messung Gegeninduktivität
Version 4
SHEET 1 880 680
WIRE -192 176 -288 176
WIRE -64 176 -112 176
WIRE 112 176 -64 176
WIRE 368 176 160 176
WIRE -288 192 -288 176
WIRE 112 192 112 176
WIRE 160 192 160 176
WIRE -288 288 -288 272
WIRE 368 304 368 176
WIRE 112 320 112 272
WIRE 128 320 112 320
WIRE 160 320 160 272
WIRE 160 320 128 320
WIRE -208 464 -304 464
WIRE -80 464 -128 464
WIRE 96 464 -80 464
WIRE 256 464 144 464
WIRE 352 464 256 464
WIRE -304 480 -304 464
WIRE 96 480 96 464
WIRE 144 480 144 464
WIRE -304 576 -304 560
WIRE 144 608 144 560
WIRE 96 640 96 560
WIRE 352 640 352 464
WIRE 352 640 96 640
FLAG -288 288 0
FLAG 368 304 0
FLAG -64 176 U11
FLAG -304 576 0
FLAG -80 464 U12
FLAG 144 608 0
FLAG 128 320 U2x
FLAG 256 464 U2
SYMBOL ind2 128 176 M0
SYMATTR InstName L1
SYMATTR Value 100�
SYMATTR Type ind
SYMBOL ind2 144 288 M180
WINDOW 0 36 80 Left 2
WINDOW 3 36 40 Left 2
SYMATTR InstName L2
SYMATTR Value 900�
SYMATTR Type ind
SYMBOL voltage -288 176 R0
WINDOW 123 24 124 Left 2
WINDOW 39 0 0 Left 2
SYMATTR Value2 AC 1
SYMATTR InstName V1
SYMATTR Value SINE(0 1 10000)
SYMBOL res -96 160 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 10
SYMBOL ind2 112 464 M0
SYMATTR InstName L3
SYMATTR Value 100�
SYMATTR Type ind
SYMBOL ind2 128 576 M180
WINDOW 0 36 80 Left 2
WINDOW 3 36 40 Left 2
SYMATTR InstName L4
SYMATTR Value 900�
SYMATTR Type ind
SYMBOL voltage -304 464 R0
WINDOW 123 24 124 Left 2
WINDOW 39 0 0 Left 2
SYMATTR Value2 AC 1
SYMATTR InstName V2
SYMATTR Value SINE(0 1 10000)
SYMBOL res -112 448 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R2
SYMATTR Value 10
TEXT 80 152 Left 2 !K1 L1 L2 1
TEXT -312 336 Left 2 !.tran 1000u
TEXT -392 384 Left 2 ;This example schematic is supplied for informational/educational purposes only.
TEXT -288 104 Left 2 ;A transformer with two windings, 1 to 3 turns winding ratio
TEXT -160 336 Left 2 !;ac dec 10 1 1000k
TEXT 64 440 Left 2 !K3 L3 L4 1
\( \underline{U}_1 ( \omega ) = j \omega L_1 \cdot \underline{I}_1
+ j \omega M \cdot \underline{I}_2 \)
\( \underline{U}_2 ( \omega ) = j \omega M \cdot \underline{I}_1
+ j \omega L_2 \cdot \underline{I}_2 \)
\( U = \omega L I = 2 \pi f L I \)
\( L = \frac{U}{2 \pi f I} \)
1) Reihenschaltung A: I1 = I2
2) Reihenschaltung B: I1 = -I2
(1) U1A = w(L1+M) IA
(2) U2A = w(L2+M) IA
(3) U1B = w(L1-M) IB
(4) U2B = w(L2-M) IB
(1)+(3)
\(\frac{U_{1A}}{\omega I_A} + \frac{U_{1B}}{\omega I_B} = L1+M+L1-M = 2 L1 \)
(1)-(3) L1+M-L1+M = 2 M
(2)+(4) L2+M+L2-M = 2 L2
(2)-(4) L2+M-L2+M = 2 M
LTSPICE Transformatorwicklungsstart wird mit kleinem Kreis markiert.
Die Berechnung von L und M ist vertauscht: (1)+(3) ergibt 2 M,
(1)-(3) ergibt L1, (2)+(4) ergibt 2 L2, (2)-(4) ergibt 2 M.
I1 = 9.6 mA, I2 = 37 mA, U1A = U11-U2 = 0.247 V, U2A = U2X = 0.74 V,
U1B = U12 - U2 = 0.46 V, U2B = U2 = 1.38 V.
f = 1 kHz
Berechnung
L1 = 106 uH, L2 =910 uH, M = 303.7 uH, M = 316.6 uH
Beispiel: Messung vom T-Ersatzschaltbild
- Spezifikation (50 Hz Einphasentransformator)
- U1N = 2 kV ( primäre Nennspannung)
- U2N = 220 V ( sekundäre Nennspannung)
- SN = 20 kVA ( Nennscheinleistung)
- Leerlaufmessung bei Nennspannung U1N, U2N:
-
P1L = 200 W (Wirkleistung), I1L = 1 A (Strommessgerät)
- Kurzschlussversuch:
- Datenblatt: \( I_K = I_N = \frac{S_N}{U_{1N}} = \frac{20 kVA}{2 kV} = 10 A \)
- Messung: P1K = 300 W, U1K = 120 V = 0.06 U1N
- Primär und Sekundärwicklung haben das gleiche Volumen.
- Die Induktivitäten und Widerstände sollen Näherungsweise berechnet werden.
- Wie groß ist der Wirkungsgrad bei Nennbelastung?
Beispiel: Kupferwiderstände
Leistungstransformator:
\( \sqrt{\frac{L_1}{L_2}} = \frac{N_1}{N_2} = ü = \frac{U_{1N}}{U_{2N}} = 9.1 \)
Annahme: \( R_1 \lt \lt R'_E \), \( R'_2 \lt \lt R'_E\), \(L_\sigma \lt \lt M' \)
Gleich große Spulenvolumina: Es soll gezeigt werden \( R_1 = ˜R‘_2 \)
\( N_2 = \frac{U_{N2}}{U_{N1}} \), \( N_1 = \frac{220}{2000} N_1 = 0.11 N_1 \)
Der Spulendraht der Primärspule ist \( \frac{1}{0.11} = 9.1 \) mal so lang,
wie der Draht der Sekundärspule. Da die Volumina gleich sein sollen,
muss der Querschnitt der Sekundärspule 9.1 mal größer sein.
\( R_2 = \rho_{Cu} \frac{l_2}{A_2} = \rho_{Cu} \frac{l_1}{9.1^2 A_1}
= \frac{R_1}{9.1^2} = \frac{R_1}{ü^2} \)
\( R‘_2 = ˜R_2 \cdot ü^2 = R_1 \)
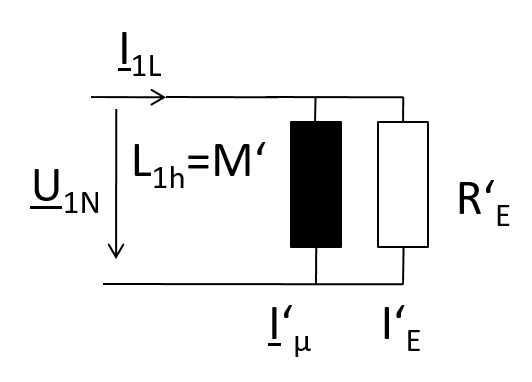
Beispiel: Leerlauf R'E, L1h=M'
Leerlauf: \( R_1 \lt \lt R‘_E \)
\( P_{1L} = \frac{U_{1N}^2}{R‘_E} \)
\( R‘_E = \frac{U_{1N}^2}{P_{1l}} = ˜\frac{(2 \cdot 10^{3} V)^2}{200 W} \)
\( R‘_E = 20 k\Omega \)
\( I‘_E = \frac{ U_{1N}}{R‘_E} = \frac{2kV}{20k\Omega} = 100 mA \)
\( \underline{I}_{1L} = \underline{I‘}_E + \underline{I‘}_\mu
= \underline{I‘}_E + j I‘_\mu \)
\( I‘_\mu = \sqrt{I_{1L}^2 - I‘_E^2} = 995 mA\)
\( \omega M‘ = \frac{U_{1N}}{I‘_\mu} = \frac{2 kV}{995 mA} = \omega M‘ = 2.01 k\Omega \)
\( L_{1h} = M‘ = \frac{2.01 k\Omega}{ 2 \pi 50 Hz} = 6.4 H\)
|
|
P1L = 200 W
U1N = U1L = 2 kV
I1L = 1 A
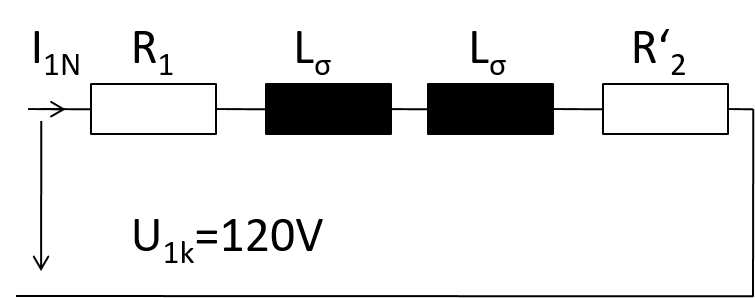
Beispiel: Kurzschluss R1, Lσ
Kurzschluss: \( R‘_2 \lt \lt R‘_E \)
\( P_{1k} = I_{1N}^2 (R_1+R‘_2)
˜= I_{1N}^2 2 R_1 \)
\( R_1 = \frac{P_{1k}}{2 I_{1N}^2}
= \frac{300 W}{2 \cdot (100 A)^2} \)
\( R_1 = 1.5\Omega \)
\( R‘_2 = 1.5\Omega\)
\( Z_{1k} = \frac{U_{1k}}{I_{1N}} = ˜ \sqrt{ (\omega L_\rho)^2 + R_1^2 } \)
\( \omega L_\rho = \sqrt{\frac{1}{4} \left(\frac{U_{1k}}{I_{1N}} \right)^2 - R_1^2 }
= \sqrt{6^2-1.5^2} \Omega = 5.8 \Omega \)
\( L_\sigma = \frac{ 5.8 \Omega }{ 2 \pi 50 Hz} = 18.5 mH \)
|
|
P1K = 300 W
I1N = 100 A
U1K = 120 V
Beispiel: Wirkungsgrad
Nennbelastung: I
1N = 10 A an R
1 und R‘
2
Kupferverluste: \( P_{Cu} = I_{1N}^2 (R_1+R‘_2) = 300 W \)
Eisenverluste: P
E = P
1L = 200W
Wirkungsgrad:
\( \eta = \frac{P_N }{P_N + P_E + P_{Cu}} \)
\( \eta = \frac{ 20kW}{ 20 kW + 0.2 kW + 0.3 kW} = 0.976 \)
Beispiel: Nachdenken über die Lösung
- Leerlauf :
- Hauptinduktivität LH
- Eisenverluste RE
- Kurzschluß :
- Streuinduktivität Lσ<\sub>
- Kupferverluste R1
- Wirkungsgrad:
- Kupferverluste, Eisenverluste
- Annahmen:
- Annahme: \( R_1 \lt \lt R'_E \), \( R'_2 \lt \lt R'_E\), \(L_\sigma \lt \lt M' \)
- R‘2 = R2 ü^2 = R1
- R1 << R‘E
Realer Transformator
- Wicklungen Widerstände (Kupferverluste)
- Eisenkern hat Wirbelstromverluste
- Ummagnetisierung des Kerns braucht Energie (Hystereseverluste)
- Streuflüsse des magnetischen Flusses F
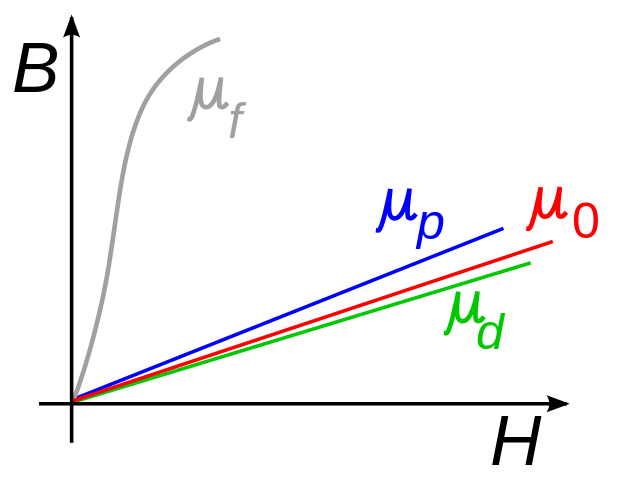
- Permeabilität hängt von Frequenz und Stärke des Magnetfeldes ab
- Sättigungseffekte des Kerns
- Einschaltstrom kann ein vielfaches des Nennstromes betragen
- Magnetostriktion Netzbrummen
Dimensionierung von Transformatoren
- Sättigungsflußdichte des verwendeten Eisens
- Stromdichte des verwendeten Drahtes
\( u_2 = N_2 \frac{d \Phi}{dt} = N_2 \frac{d \hat{\Phi} sin\omega t}{dt}
= N_2 \omega \hat{\Phi} cos\omega t\)
\( \hat{u}_2 = N_2 \cdot 2 \cdot \pi \cdot f \cdot \hat{\Phi}
= N_2 \cdot 2 \cdot \pi \cdot f \cdot A \hat{B} \)
\( U_2 = N_2 \frac{2 \pi}{\sqrt{2}} \cdot f \cdot A \cdot B \) Effektivwert
\( B = \frac{U_2}{4.44 \cdot f \cdot N_2 \cdot A} \)
Durch die Frequenz f, die Wicklungszahl N_2 und dem Querschnitt A wird das maximale B bestimmt.
Für ein Schaltnetzteil ist f groß und damit kann A und das Netzteil klein werden.
Φ magnetischer Fluss, A Querschnitt Kern, B magnetische Flussdichte, f Betriebsfrequenz
