Grundlagen Elektrotechnik 2 (GET2)

25 Drehstrom

Prof. Dr. Jörg Vollrath

24 Transformator

Übersicht

Letztes Mal:
Transformator
Heute:
Drehstrom
Dreileitersystem
Leistung

Das Bild zeigt eine Strommast mit 3 Leitern rechts und 3 Leitern links.
Eine typische 3 Phasen Übertragung.

Das symmetrische Dreiphasensystem

Einphasensystem
Haushaltsspannung
Eine Hin und eine Rückleitung
Mehrphasensystem
Mehr als 2 Strombahnen
Teil mit einem einheitlicher Schwingungszustand des Stromes: Strang
In den verschiedenen Strängen gleiche Frequenz unterschiedliche Nullphasenwinkel
Dreiphasensystem (three phase system)
Drei Stränge
Drehstromsystem
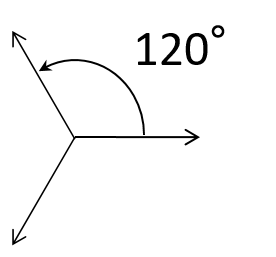
Symmetrisch : Amplituden gleich, 120° unterschiedliche Nullphasenwinkel

Drehstrom

Amplituden gleich
120° unterschiedliche Nullphasenwinkel
\( \underline{U}_1 = U \)
\( \underline{U}_2 = U \underline{/-120°}\)
\( \underline{U}_3 = U \underline{/120°}\)

Summe symmetrischer Größen

\( \underline{U}_1 = U \)
\( \underline{U}_2 = U (-0.5 - j 0.866) \)
\( \underline{U}_3 = U (-0.5 + j 0.866) \)
\( \underline{U}_1 + \underline{U}_2 + \underline{U}_3 = 0 \)
Die Summe von drei symmetrischen Größen ist stets null

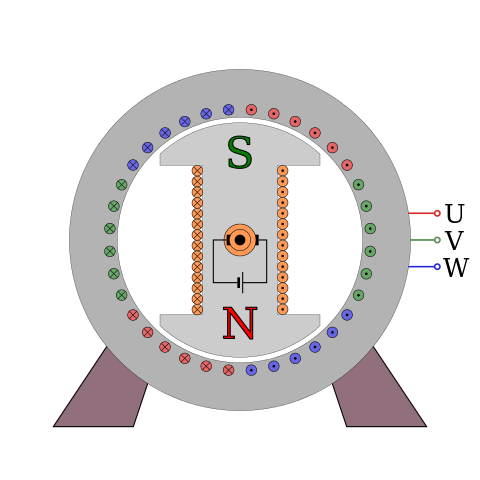
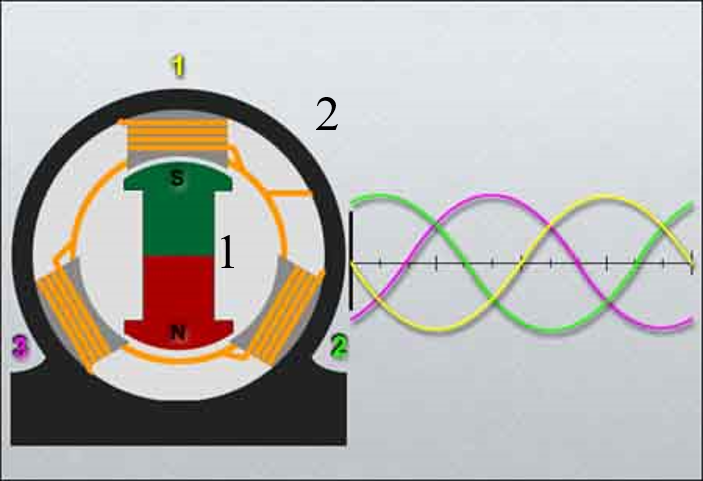
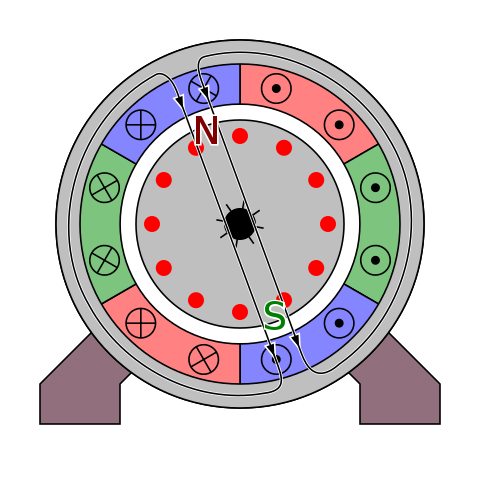
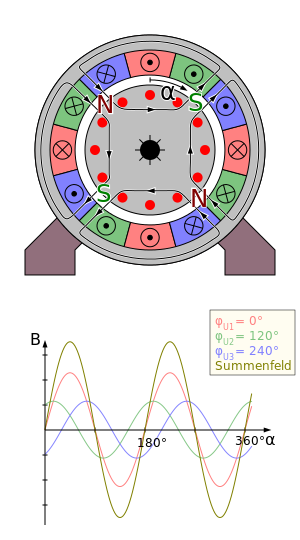
Synchrongenerator

(1) Läufer
Permanentmagnet
Erregerwicklung
Polrad
(2) Ständerwicklung
Bezeichnung Strang
Anfang: U1, V1, W1
Ende: U2, V2, W2
Anker
Teil in dem eine Spannung induziert wird
Synchronmaschine: Ständer
Ankerrückwirkung durch Belastungsstrom

Sternschaltung (star connection)

Verbindung

U2, V2, W2

Knoten N

Sternpunkt (neutral point)
Sternpunktleiter

Außenpunkte

U1, V1, W1
Außenleiter
L1, L2, L3
Früher (R, S, T)

Vierleitersystem mit N
Dreileitersystem ohne Verbindung N

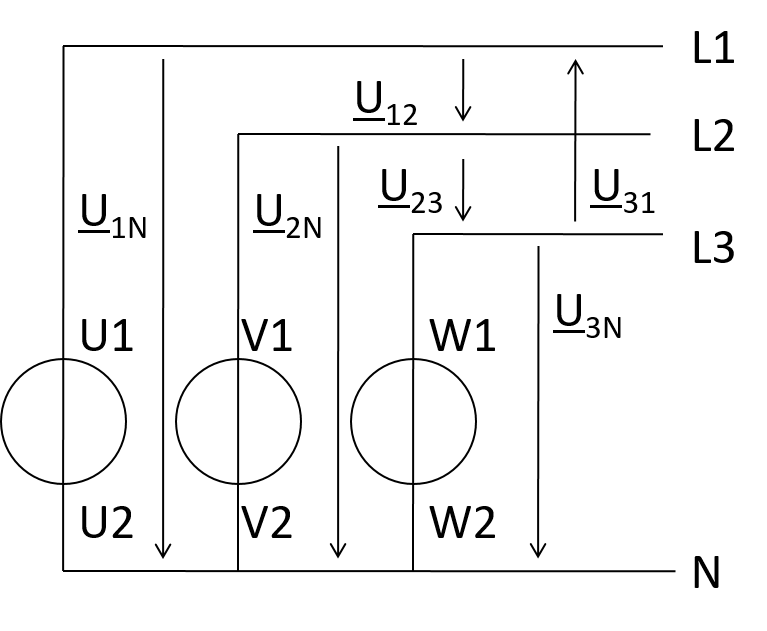Außenleiterspannung

\( \underline{U}_{12} = \underline{U}_{1N} - \underline{U}_{2N} = U - U(-0.5 – j 0.866) = 1.5 U + j 0.866 U\)
\( \underline{U}_{12} = \sqrt{3} U \underline{/30°} \)

\( \underline{U}_{12} = \sqrt{3} U \underline{/30°} \)

Spannungsversorgung:
U1N = U2N = 230 V
U12 = 400 V

Sternschaltung

Strangspannungen vier Leiter System

Sternspannung Effektivwert der Strangspannung
\( \underline{U}_{1N} \), \( \underline{U}_{2N} \), \( \underline{U}_{3N} \)
Phasenfolge
Zeitliche Aufeinanderfolge der Phasen
\( \underline{U}_{2} \) eilt \( \underline{U}_{1} \) nach Mitsystem

Außenleiterspannung

\( \underline{U}_{12} = \underline{U}_{1N} - \underline{U}_{2N} = \sqrt{3} U \underline{/30°} \)
\( \underline{U}_{23} = \underline{U}_{2N} - \underline{U}_{3N} = \sqrt{3} U \underline{/-90°} \)
\( \underline{U}_{31} = \underline{U}_{3N} - \underline{U}_{1N} = \sqrt{3} U \underline{/150°} \)
Die Außenleiterspannung ist in einem symmetrischen Drehstromsystem um den Faktor \( \sqrt{3} \) größer als die Sternspannung

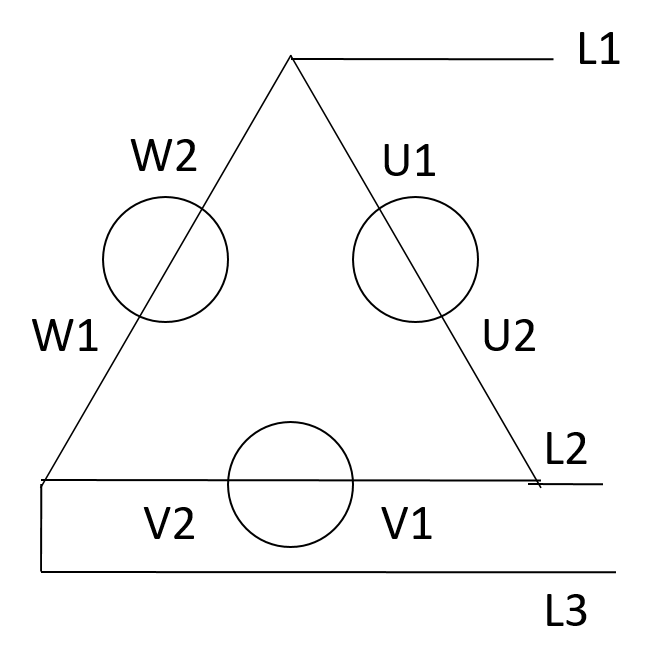
Dreieckschaltung (Delta connection)

Nur der Außenleiter vorhanden
Bei Generatoren nicht angewendet, da sich hierbei Oberschwingungen störend auswirken
Transformator zwischen Generator und Übertrager
Dreieckspannung ist in einem symmetrischen Drehstromsystem gleich dem Effektivwert einer Außenleiterspannung

Leistung im Drehstromsystem

Sternschaltung

Strangströme

\( \underline{I}_1 = \frac{\underline{U}_{1N}}{\underline{Z}} = \frac{U_{str}}{Z} \underline{/-\phi} \)
\( \underline{I}_2 = \frac{\underline{U}_{2N}}{\underline{Z}} = \frac{U_{str}}{Z} \underline{/-120°-\phi} \)
\( \underline{I}_3 = \frac{\underline{U}_{3N}}{\underline{Z}} = \frac{U_{str}}{Z} \underline{/120°-\phi} \)

Sternstrom

\( I = \frac{Ustr}{Z} \)

Strom \( \underline{I}_N \):

\( \underline{I}_N = \underline{I}_1 + \underline{I}_2 + \underline{I}_3 = 0 \)

Bei symmetrischer Belastung fließt kein Strom
Der Sternpunktleiter kann bei symmetrischer Belastung entfallen.

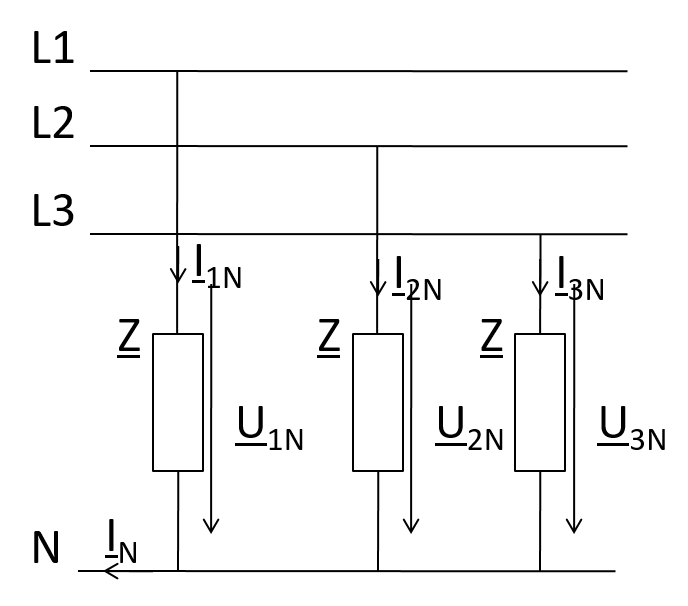Sternschaltung und Strangleistung

\( P(t) = \sqrt{2} U_{str} cos(\omega t) \cdot \sqrt{2} I_{str} cos(\omega t - \phi) \cdot + \sqrt{2} U_{str} cos(\omega t - 120°) \cdot \sqrt{2} I_{str} cos(\omega t - \phi - 120°) \cdot + \sqrt{2} U_{str} cos(\omega t + 120°) \cdot \sqrt{2} I_{str} cos(\omega t - \phi + 120°) \cdot\)

\( cos\alpha \cdot cos\beta = 0.5 cos(\alpha - \beta) + 0.5 cos(\alpha + \beta) \)

\( P(t) = U_{str} I_{str} cos(\phi) + U_{str} I_{str} cos(2 \omega t - \phi) U_{str} I_{str} cos(\phi) + U_{str} I_{str} cos(2 \omega t - 240° - \phi) U_{str} I_{str} cos(\phi) + U_{str} I_{str} cos(2 \omega t + 240° - \phi) \)

\( P(t) = 3 U_{str} I_{str} cos(\phi) \)

Die gesamte Wirkleistung ist konstant

Konstante Leistung -> konstantes Drehmoment
Rotierende Drehstrommaschinen

Strangleistung zeitabhängig:
\( P_{str}(t) = U_{str} I_{str} cos(\phi) + U_{str} I_{str} cos(2 \omega t - \phi) \)

Beispiel

Ein in Stern geschalteter Motor wird am 400 V Drehstromnetz mit f = 50Hz betrieben.
In jedem Strang befindet sich ein Widerstand R = 24 Ω in Reihe mit einer Induktivität L = 44.6 mH.
Der Außenleiterstrom und die Leistung, die der Motor aufnimmt, sollen berechnet werden.

Vergleich: Stern und Dreieck

Größe	Stern	Dreieck
Strangspannung	U_Str	U_Dre
Strangstrom	I_Str	I_Dre
Außenleiterspannung	\( U = \sqrt{3} U_{Str} \)	\( U = U_{Dre} \)
Außenleiterstrom	\( I = I_{str} \)	\( I = \sqrt{3} I_{Dre} \)
Komplexe Leistung	\( S = \sqrt{3} U I \underline{/\phi} \)	\( S = \sqrt{3} U I \underline{/\phi} \)
der drei Stränge	\( S = 3 U_{Str} I_{Str} \underline{/\phi} \)	\( S = 3 U_{Dreh} I_{Dreh} \underline{/\phi} \)

Anzahl der Pole	Polpaarzahl p	α	Drehzahl bei 50 Hz 1/s	Drehzahl bei 50Hz 1/min
2	1	120°	50	3000
4	2	60°	25	1500
6	3	40°	16.67	1000
8	4	30°	12.5	750
10	5	24°	10	600
12	6	20°	8.33	500

2022 GET 2 25 Drehstrom Prof. Dr. Joerg Vollrath

Grundlagen Elektrotechnik 2 (GET2)

25 Drehstrom

Prof. Dr. Jörg Vollrath

Video der 19. Vorlesung 8.6.2021

Übersicht

Das symmetrische Dreiphasensystem

Drehstrom

Summe symmetrischer Größen

Synchrongenerator

Sternschaltung (star connection)

Außenleiterspannung

Sternschaltung

Dreieckschaltung (Delta connection)

Leistung im Drehstromsystem

Sternschaltung

Sternschaltung und Strangleistung

Beispiel

Vergleich: Stern und Dreieck

Polpaarzahl und Drehfeldzahl

Praxisbezug

Zusammenfassung und nächstes Mal