Interface Electronics 06 DAC Architectures and Error Prof. Dr. Jörg Vollrath 05 DAC Architectures

Review and Overview

Review:

• RC requirements
• DAC architectures
• R string DAC
• Interpolating DAC
  
• Parallel charge scaling DAC
• Equivalent sources
• Split array charge scaling DAC
• R2R DAC

Today:

• Realization of capacitances
• Example: R-string DAC
• Statistical resistor and capacitor variations: INL and DNL
• Switches, opamps and performance

Resistor string DA converter with mismatch

A real 3-Bit resistor string DA converter with Vref= 4V has some error due to R mismatch. The switches are closed when the control signal is ‘1’. b signals are the inverted signals. What is the maximum output voltage and the average step size? (3 points) Fill the table for the transfer function, the INL and DNL ? Code 000 001 010 011 100 101 110 111 Vout[V] INL[LSB] DNL[LSB] Vmax = Vref/800*700 = 3.5V LSB = 4V/8 = 0.5V Code 000 001 010 011 100 101 110 111 Vout[V] 0 0.4 0.9 1.55 2.05 2.55 3.0 3.5 INL[LSB] 0 -0.2 -0.2 0.1 0.1 0.1 0 0 DNL[LSB] -0.2 0 0.3 0 0 -0.1 0

Limits for DAC scaling

• DAC scaling limits
  • resolution, sample rate, power
• DAC architectures
  • R2R, C2C, ladder, unit element, current source
• Resolution
  • Noise, leakage, mismatch, voltage and temperature variation
• Sample rate
  • RC time constant

Mismatch and probability density

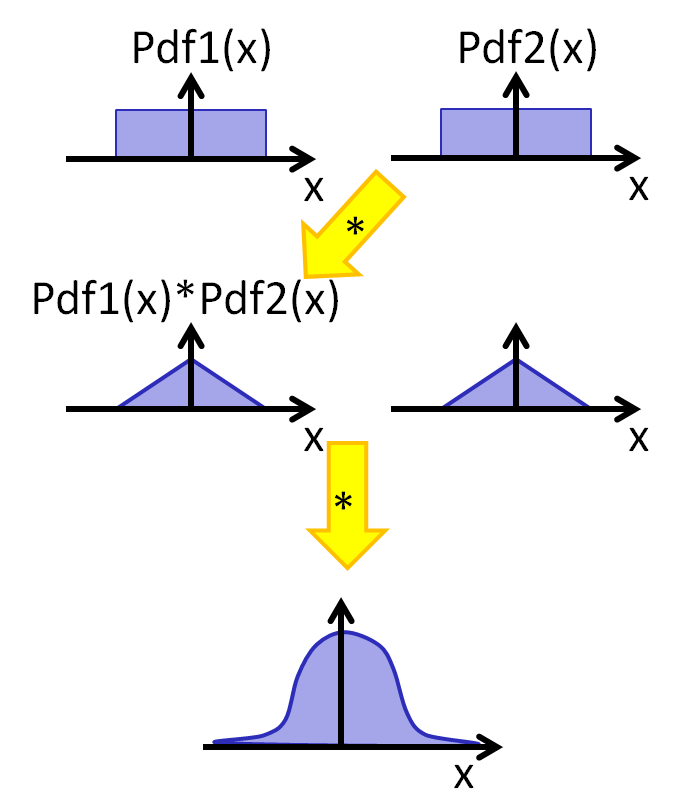
Real components have random variations Discrete resistors: 0.1%, 1%, 10% Integrated resistors: Manufacturing step variations Model for random variations: Probability density function Constant probability of variation. Mixing of probability functions gives a gaussian distribution

Gaussian distribution

Equation: \( p(x) = \frac{1}{\sigma \sqrt{2 \pi }} e^{- \frac{1}{2} \left( \frac{x-\mu}{\sigma} \right)^2 } \) µ expected value σ standard deviation σ2 variance This distribution has no bounds. The higher the number of components, more components are out of a certain bound. Manufacturing a resistance or capacitance will also result in variations of value. This causes INL and DNL errors for data converter and can lead to bad faulty devices. Width of two, four and six standard deviations have 68.27%, 95.45% and 99.73% of the population.

Realization

In integrated circuits all elements have a gaussian distribution around the designed value. Since good data converters must meet strict requirements for INL and DNL, high variations of circuit elements can cause bad INL and DNL. What variation of circuit elements can be tolerated? How does mismatch influence INL and DNL? R-string: unit elements R2R, C2C binary weighted Example: 0.1% resistor tolerance

Unit element mismatch and DNL

Only random error: Iref: reference current Rnom: nominal resistance \( \Delta_i = I_{ref} \cdot R_i \) \( DNL_{i} = \frac{\Delta_i - \Delta}{\Delta} = \frac{ R_i - R_{nom}}{R_{nom}} \approx \frac{dR}{R_i} \) \( \sigma_{DNL} = \sigma_{R} \) 1% tolerance in resitance gives 1% = 0.01 DNL.

Unit element mismatch and INL: Theory

Only random error: E: Error at code x N: Number of maximum code A: Real output Ideal Variance A = x + E x x · σε2 B = N - x - E N - x (N - x) · σε2 Ratio: \( r = \frac{x}{N} \) N = A + B E = A - x = A - r · N = A - r · (A + B) = (1 - r) · A - r · B Variance at code x: \( \sigma_{INL}^2 = (1 - r)^2 \cdot \sigma_{A}^2 + r^2 \sigma_{B}^2 \) \( \sigma_{INL}^2 = (1 - r)^2 \cdot x \cdot \sigma_{\epsilon}^2 + r^2 \cdot (N-x) \cdot \sigma_{\epsilon}^2 \) \( \sigma_{INL}^2 = (x - 2 \cdot x \cdot r + x \cdot r^2 + r^2 \cdot N - x \cdot r^2) \cdot \sigma_{\epsilon}^2 \) \( \sigma_{INL}^2 = (x - 2 \cdot \frac{x^2}{N} + \frac{x^2}{N} ) \cdot \sigma_{\epsilon}^2 \) \( \sigma_{INL}^2 = (x - 2 \cdot \frac{x^2}{N} + \frac{x^2}{N} ) \cdot \sigma_{\epsilon}^2 \) \( \sigma_{INL}^2 = x \cdot \left( 1 - \frac{x}{N} \right) \cdot \sigma_{\epsilon}^2 \)

Unit element mismatch and INL

Only random error: \( \sigma_{INL}^2(x) = x (1 - \frac{x}{N}) \cdot \sigma_{\epsilon}^2 \) \( \sigma_{INL}(x) = \sqrt{x (1 - \frac{x}{N})} \cdot \sigma_{\epsilon} \) Maximum: \( \frac{\sigma_{INL}^2}{dx} = 0 \) \( 1 - \frac{2 x}{N} = 0 \) \( x = \frac{N}{2} \) \( \sigma_{INLmax} = \sqrt{\frac{N}{2} (1 - \frac{N}{2 \cdot N})} \cdot \sigma_{\epsilon} \) \( \sigma_{INLmax} = \frac{1}{2} \sqrt{ N } \cdot \sigma_{\epsilon} = \frac{1}{2} \sqrt{ 2^{B} -1 } \cdot \sigma_{\epsilon} \)

Example: N = 63

Binary weighted DAC DNL and INL

INL same as unit element INL. \( \sigma_{INLmax} = \frac{1}{2} \sqrt{ 2^{B} -1 } \cdot \sigma_{\epsilon} \approx \frac{1}{2} \cdot 2^{\frac{B}{2}} \cdot \sigma_{\epsilon}\) Switching in the center: Half devices on, half minus one devices off DNL: Switching at center position: 011111..100000 \( \sigma_{DNLmax}^2 = \left( 2^{B-1} - 1 \right) \cdot \sigma_{\epsilon}^2 + \left( 2^{B-1} \right) \cdot \sigma_{\epsilon}^2 \) \( \sigma_{DNLmax} \approx 2^{\frac{B}{2}} \cdot \sigma_{\epsilon} = 2 \sigma_{INLmax} \)

Comparison INL and DNL: Binary weighted versus unit elements

Binary weighted topology R2R: \( \sigma_{INLmax} \approx \frac{1}{2} \cdot 2^{\frac{B}{2}} \cdot \sigma_{\epsilon}\) DNL: \( \sigma_{DNLmax} \approx 2^{\frac{B}{2}} \cdot \sigma_{\epsilon} \) \( \sigma_{DNLmax} \approx 2 \sigma_{INLmax} \) B, 2B, 3B elements

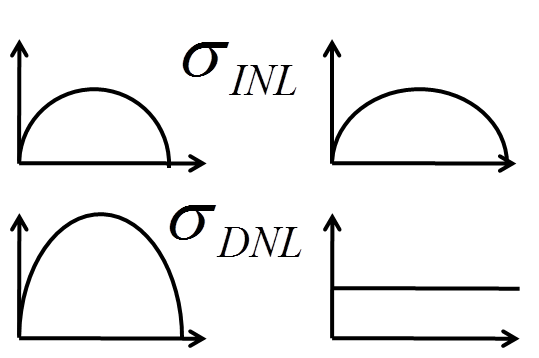Unit element topology R-string: \( \sigma_{INLmax} \approx \frac{1}{2} \cdot 2^{\frac{B}{2}} \cdot \sigma_{\epsilon}\) DNL: \( \sigma_{DNLmax} = \sigma_{\epsilon} \) 2B elements

Motivation of segmented DAC with MSB unit elements and LSB with binary weights.

Publication: Simulation of INL and DNL

Javascript Simulation DAC Error

C. Lin and K. Bult, "A 10-b,500-MSample/sCMOS DAC in 0.6mm2," IEEEJournal ofSolid-StateCircuits, vol.33, pp. 948- 1958,December1998.

Simulation of 100 runs of unit and binary 10 bit DAC with random variations with a σ_εof 2 %.

Plots of INL and DNL showed expected shape of distribution.

RMS of simulation showed the expected values for INL and DNL.

Motivation of segmented DAC with MSB unit elements and LSB with binary weights.

A LTSPICE simulation example with a 3-bit unit element DAC and a 3 and 4-bit binary DAC can be done to look at DNL and INL error.

Realization of resistors and capacitances

Process variables:

Undercutting Non uniformities Unit elements Ratio area to edge is constant. Common centroid design Systematic vertical and horizontal variations cancel out. Dummy elements

Capacitances

Resistors

Test and Calibration

Calibration

• Element trimming (laser fuse) at the end of wafer fabrication
• Inverse equation
• Lookup table
• Online background calibration

Test and strategy for calibration

• Identify topology: unit or binary weighted
• Unit elements
• Binary weighted elements
• Start in the center with biggest error

Laboratory and Calibration

How much can digital calibration do for a binary weighted DAC?

• Measure DNL and INL
• For big steps in output voltage, DNL large, change capacitances.
  Jump at step 64, change capacitances at input D5 with a capacitance between D4 and D5.
• Negative steps or negative DNL create an equation
  if (code && 128) { code = code + x }
• Create new calibrated input code ramp and measure INL and DNL again.
• Create new calibrated input code for sine input signal and measure FFT, INL and DNL again.

Summarize your experience.

DAC digital calibration example

Code 0 1 2 3 4 5 6 7 Vreal [V] 0 1.5 3 1.8 5 6 6.5 7 Videal [V] 0 1 2 3 4 5 6 7 INL 0 0.5 1 -1.2 1 1 0.5 0 DNL 0.5 0.5 -2.2 2.2 0 -0.5 -0.5 LSB = 1 V Slope Reversal Change Remove/reorder code 3,6 Adjust step size

DAC digital calibration example result

LSB =1 V Code range: 0..7 Lookup table, equation Code 0 1 1 3 2 4 5 7 CodeX 0 1 2 3 4 5 6 7 Vreal [V] 0 1.5 1.5 1.8 3 5 6 7 Videal [V] 0 1 2 3 4 5 6 7 INL 0 0.5 -0.5 -1.2 -1 0 0 0 DNL 0.5 -1 -0.7 0.2 1 0 0

DAC digital calibration example result

LSB =1.4 V Code range: 0..5 No power of 2! Lookup table, equation Code 0 1 2 3 4 5 6 7 CodeX 0 1 2 3 4 5 Vreal [V] 0 1.5 3 1.8 5 6 6.5 7 Videal [V] 0 1.4 2.8 4.2 5.6 7 INL 0 0.07 0.14 0.57 0.29 0 DNL 0.07 0.07 0.43 -0.29 -0.29

DAC digital calibration: 1 bit reduction

LSB =2.33 V Code range: 0..3 Lookup table, equation Code 0 1 2 3 4 5 6 7 CodeX 0 1 2 3 Vreal [V] 0 3 5 7 Videal [V] 0 2.33 4.67 7 INL 0 0.29 0.14 0 DNL 0.29 -0.14 -0.14

DAC digital calibration: 1 bit reduction

LSB =2 V Code range: 0..3 Lookup table, equation Code 0 1 2 3 4 5 6 7 CodeX 0 1 2 3 Vreal [V] 0 1.5 3 6 Videal [V] 0 2 4 6 INL 0 -0.25 -0.5 0 DNL -0.25 -0.25 0.5

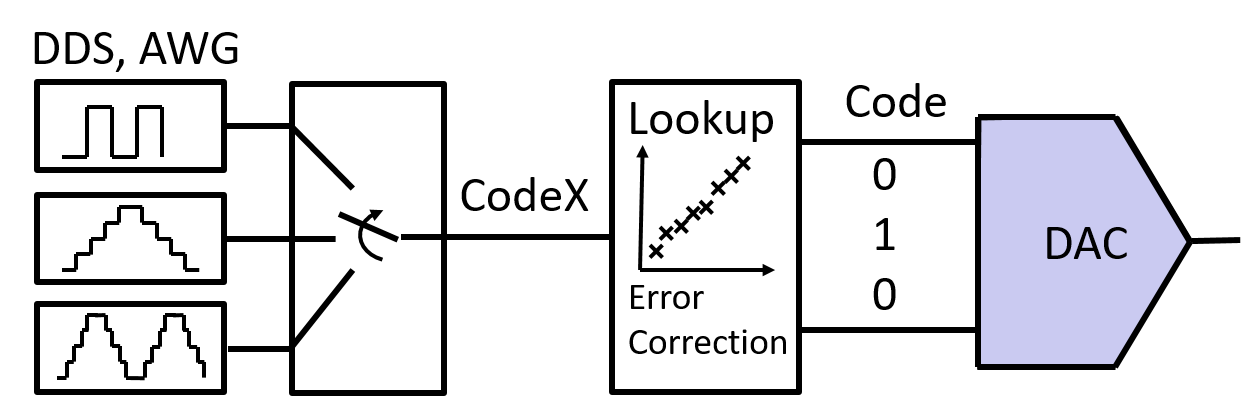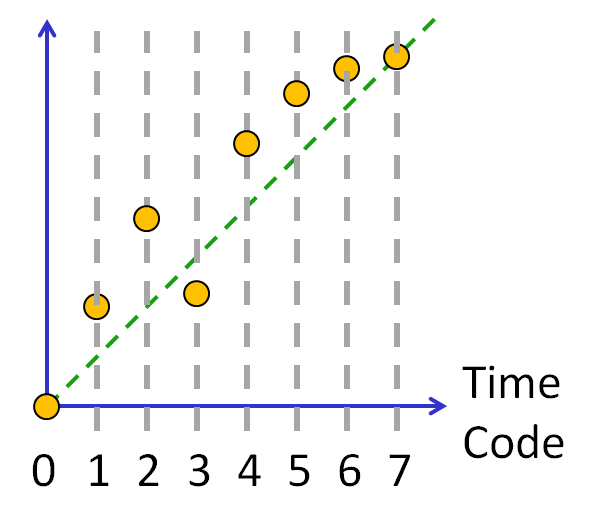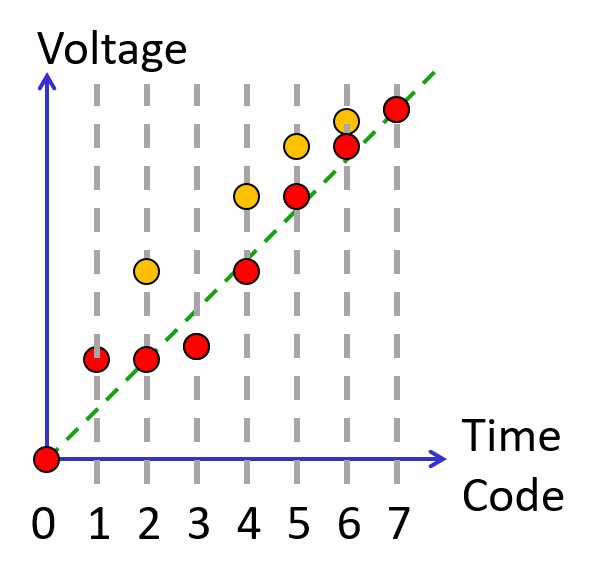
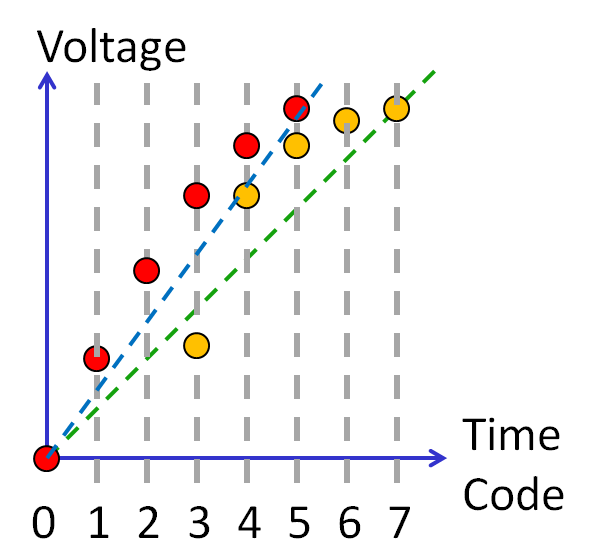
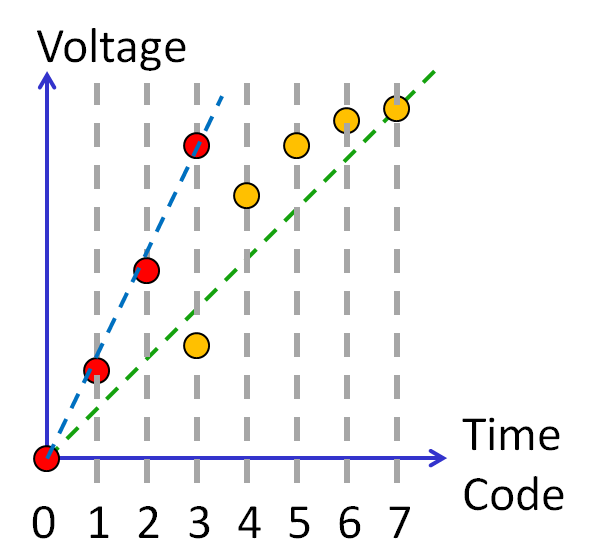
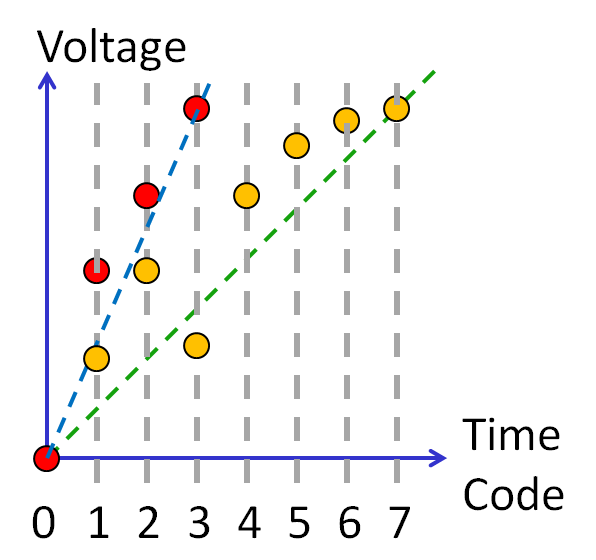DAC digital calibration summary

Digital calibration is possible.
Lookup table, equation
INL should be in the range of ± 1/2 LSB.
DNL should be in the range of ± 1/2 LSB( ± 1 LSB).

For a power of 2 DAC half the step size, until INL and DNL are smaller than 1/2 LSB.

Otherwise sort the values and identify the biggest step size step_max.
Depending on the other DNL values the real step size can be between 1.5 LSB = 1.5 step_max and LSB = step_max.

Since numbers are displayed in decimal some codes could be omitted for having a nice decimal step size: 10 mV, 5mV, 2 mV or a good range.
Binary decimal conversion:
1024 .. 1000
4096...4000
65536..50000

Next

07 Practical DAC examples

References

[1] "Nonlinearity analysis of resistor string A/D converters" S. Kuboki; K. Kato; N. Miyakawa; K. Matsubara IEEE Transactions on Circuits and Systems Year: 1982, Volume: 29, Issue: 6 Pages: 383 - 390
[2] "A 10-b,500-MSample/sCMOS DAC in 0.6mm2," C. Lin and K. Bult, IEEEJournal of Solid-State Circuits, Year: 1998, vol.33, December, pp. 948- 1958