Interface Electronics05 DAC ArchitecturesProf. Dr. Jörg Vollrath04 Spectral Test |
Video Lecture: DAC architectures
|
Länge: 01:06:27 |
0:00:00 Laboratory specify your .raw file directory 0:03:29 Internet copyright form 0:04:18 Laboratory 3 start 0:07:28 DAC Architecture 0:08:02 DAC Performance 0:10:51 DAC Speed voltage difference requirements 0:16:36 RC Low pass thermal noise and LSB 0:20:15 Minimum C requirement C > 12 k T 22B/VFS2 0:21:26 Maximum speed R requirement 0:23:13 RC Low pass thermal noise capacitance requirement 0:25:26 Capacitance and white noise 0:26:45 3 bit R string or ladder DAC 0:29:50 Code 011 output voltage 0:32:38 Trnasfer curve calculation 0:33:32 Speed, power, numbe rof bits, complexity 0:36:13 Power 0:39:00 Interpolating R-string DAC 0:45:39 R2R DAC 0:48:21 Equivalent voltage source 0:50:36 2nd stage D1 0:55:10 DAC in Webreport for laboratory 2 0:57:27 |
Review and Overview
- Performance
- DAC architectures
- R string DAC
- Interpolating DAC
- Parallel charge scaling DAC
- Equivalent sources
- Split array charge scaling DAC
- Realization of capacitances
- R2R DAC
- Example: R-string DAC
- Statistical errors: INL and DNL
Performance
Go from one voltage level to another between certain sampling times.At the moment we assume an ideal sample and hold circuit. Real sample and hold circuits are presented later.
A simple RC charging circuit is our model.
Performance parameters are:
- Speed: Sampling rate, bandwidth, latency
- Power
- Number of bits
- Complexity
DAC speed: voltage difference requirement
|
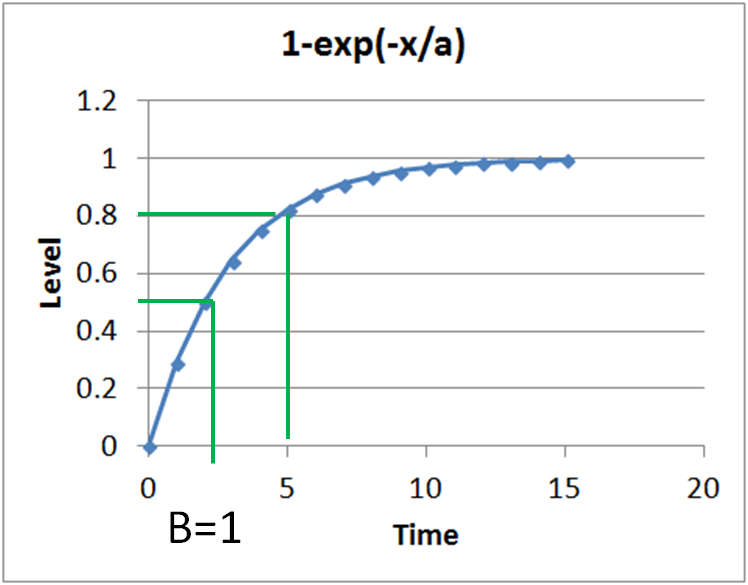
A capacitor has to be charged to the 1/2 LSB range of the input voltage: | V_e - V_a | < 0.5 LSB The voltage on the capacitor is: V_a = V_e \cdot \left( 1 - e^{-\frac{t}{\tau}} \right) with \tau = RC Maximum difference could be full scale V_e = 2^{B} \cdot LSB with B number of bits: 2^{B} \cdot LSB \cdot e^{-\frac{t}{\tau}} < 0.5 LSB -\frac{t}{\tau} < \left( -B-1 \right) ln \left( 2 \right) t > R C \left( B+1 \right) ln \left( 2 \right) |
|
Settling time: (B+1)*t1
A capacitor has to be charged to the 1/2 LSB range of the input voltage:
| V_e - V_a | < 0.5 LSB
The voltage on the capacitor is:
V_a = V_e \cdot \left( 1 - exp^{-\frac{t}{\tau}} \right) with \tau = RC
This gives:
V_e - V_e \cdot \left( 1 - exp^{-\frac{t}{\tau}} \right) < 0.5 LSB V_e \cdot e^{-\frac{t}{\tau}} < 0.5 LSB
Maximum difference could be full scale V_e = 2^{B} \cdot LSB with B number of bits:
Measurement:
Time when half level is reached: t1
Settling time: (B+1)*t1
| V_e - V_a | < 0.5 LSB
The voltage on the capacitor is:
V_a = V_e \cdot \left( 1 - exp^{-\frac{t}{\tau}} \right) with \tau = RC
This gives:
V_e - V_e \cdot \left( 1 - exp^{-\frac{t}{\tau}} \right) < 0.5 LSB V_e \cdot e^{-\frac{t}{\tau}} < 0.5 LSB
Maximum difference could be full scale V_e = 2^{B} \cdot LSB with B number of bits:
| 2^{B} \cdot LSB \cdot exp^{-\frac{t}{\tau}} < 0.5 LSB | exp^{-\frac{t}{\tau}} < 2^{-B-1} | |
| -\frac{t}{\tau} < ln \left( 2^{-B-1} \right) | -\frac{t}{\tau} < \left( -B-1 \right) ln \left( 2 \right) | |
| t > R C \left( B+1 \right) ln \left( 2 \right) |
Measurement:
Time when half level is reached: t1
Settling time: (B+1)*t1
RC low pass thermal noise
|
A resistor has a noise voltage: \frac{V_{rms}^2}{\Delta f} = 4 k_B \cdot T \cdot R A low pass RC network limits the noise to: \overline{v_n^2} = \frac{k_B T}{C} This noise has to be lower than the quantization noise: \overline{v_q^2} = \frac{\Delta^2}{12} = \frac{V_{FS}^2}{2^{2B} \cdot 12} \frac{k_B T}{C} \lt \frac{V_{FS}^2}{2^{2B} \cdot 12} \frac{C}{k_B T} \gt \frac{2^{2B} \cdot 12}{V_{FS}^2} |
|
Elektronik 3: 24 Rauschen
RC low pass thermal noise capacitance requirement
|
C \gt 12 \cdot k_B \cdot T \frac{2^{2 B}}{V_{FS}^{2}} kB: Boltzmann constant T: absolute temperature in Kelvin B: number of Bits VFS: Full scale voltage
|
\sqrt{\frac{k_B T}{C}} = \sqrt{\frac{V_{FS}^2}{2^{2B} \cdot 12}}
|
Decreasing the voltage by a factor of 3.3 increases the capacitance with a factor of 10.
3 Bit R string or ladder DAC
|
A R ladder divides VREF voltage into all possible voltage levels. Inherent monotonic Example: Input Code [d2 d1 d0] = 011 LSB = Vref/8 Vout = LSB * (0*4 + 1*2 + 1) = 3/8 Vref |
Version 4 SHEET 1 1884 680 WIRE -304 -464 -304 -480 WIRE -208 -416 -208 -448 WIRE -304 -368 -304 -384 WIRE -240 -368 -304 -368 WIRE -96 -368 -176 -368 WIRE -304 -352 -304 -368 WIRE -64 -352 -64 -448 WIRE -144 -304 -144 -448 WIRE -96 -304 -96 -368 WIRE 32 -304 -32 -304 WIRE -304 -256 -304 -272 WIRE -176 -256 -304 -256 WIRE -96 -256 -96 -304 WIRE -96 -256 -112 -256 WIRE -304 -240 -304 -256 WIRE 64 -240 64 -448 WIRE -208 -192 -208 -416 WIRE 32 -192 32 -304 WIRE 176 -192 96 -192 WIRE -304 -144 -304 -160 WIRE -240 -144 -304 -144 WIRE -96 -144 -176 -144 WIRE -16 -144 -16 -448 WIRE -304 -128 -304 -144 WIRE -96 -96 -96 -144 WIRE -48 -96 -96 -96 WIRE 32 -96 32 -192 WIRE 32 -96 16 -96 WIRE -144 -80 -144 -304 WIRE -304 -32 -304 -48 WIRE -176 -32 -304 -32 WIRE -96 -32 -96 -96 WIRE -96 -32 -112 -32 WIRE -304 -16 -304 -32 WIRE 176 16 176 -192 WIRE 240 16 176 16 WIRE 288 16 240 16 WIRE -208 32 -208 -192 WIRE 240 64 240 16 WIRE -304 80 -304 64 WIRE -240 80 -304 80 WIRE -96 80 -176 80 WIRE -64 80 -64 -352 WIRE -304 96 -304 80 WIRE -96 128 -96 80 WIRE 32 128 -32 128 WIRE -144 144 -144 -80 WIRE 240 160 240 128 WIRE -304 192 -304 176 WIRE -176 192 -304 192 WIRE -96 192 -96 128 WIRE -96 192 -112 192 WIRE 128 192 128 -448 WIRE -304 208 -304 192 WIRE 32 240 32 128 WIRE 96 240 32 240 WIRE 176 240 176 16 WIRE 176 240 160 240 WIRE -208 256 -208 32 WIRE -304 304 -304 288 WIRE -240 304 -304 304 WIRE -96 304 -176 304 WIRE -16 304 -16 -144 WIRE -304 320 -304 304 WIRE -96 352 -96 304 WIRE -48 352 -96 352 WIRE 32 352 32 240 WIRE 32 352 16 352 WIRE -144 368 -144 144 WIRE -304 416 -304 400 WIRE -176 416 -304 416 WIRE -96 416 -96 352 WIRE -96 416 -112 416 WIRE -304 432 -304 416 FLAG -304 432 0 FLAG -304 -480 VREF FLAG -208 -448 D0 FLAG -144 -448 D0b FLAG -64 -448 D1 FLAG -16 -448 D1b FLAG 64 -448 D2 FLAG 128 -448 D2b FLAG 288 16 Vout FLAG 240 160 0 SYMBOL Switch -144 416 M0 SYMATTR InstName X5 SYMBOL res -320 192 R0 SYMATTR InstName R1 SYMATTR Value 100 SYMBOL res -320 80 R0 SYMATTR InstName R2 SYMATTR Value 100 SYMBOL res -320 -32 R0 SYMATTR InstName R3 SYMATTR Value 100 SYMBOL res -320 -144 R0 SYMATTR InstName R4 SYMATTR Value 100 SYMBOL res -320 -256 R0 SYMATTR InstName R5 SYMATTR Value 100 SYMBOL res -320 -368 R0 SYMATTR InstName R6 SYMATTR Value 100 SYMBOL res -320 -480 R0 SYMATTR InstName R7 SYMATTR Value 100 SYMBOL res -320 304 R0 SYMATTR InstName R0 SYMATTR Value 100 SYMBOL Switch -208 304 M0 SYMATTR InstName X7 SYMBOL Switch -144 192 M0 SYMATTR InstName X8 SYMBOL Switch -208 80 M0 SYMATTR InstName X9 SYMBOL Switch -144 -32 M0 SYMATTR InstName X10 SYMBOL Switch -208 -144 M0 SYMATTR InstName X11 SYMBOL Switch -144 -256 M0 SYMATTR InstName X12 SYMBOL Switch -208 -368 M0 SYMATTR InstName X13 SYMBOL Switch -64 128 M0 SYMATTR InstName X14 SYMBOL Switch -64 -304 M0 SYMATTR InstName X15 SYMBOL Switch -16 -96 M0 SYMATTR InstName X16 SYMBOL Switch -16 352 M0 SYMATTR InstName X17 SYMBOL Switch 64 -192 M0 SYMATTR InstName X18 SYMBOL Switch 128 240 M0 SYMATTR InstName X19 SYMBOL cap 224 64 R0 SYMATTR InstName C1 SYMATTR Value 1p TEXT -352 -584 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1123u VT0=0.5 LAMBDA=0.018)\n.model CD4007P PMOS(LEVEL=1 KP=1123u VT0=-0.5 LAMBDA=0.018) TEXT 168 -504 Left 2 !.global VDD\n.include opamp.sub\nV4 d2b 0 PULSE(0 5 0 1n 1n 3999n 8000n)\nV1 d2 0 PULSE(5 0 0 1n 1n 3999n 8000n) TEXT 232 -144 Left 2 !.tran 18000n TEXT 160 -392 Left 2 !V2 d0b 0 PULSE(0 5 0 1n 1n 999n 2000n)\nV5 d0 0 PULSE(5 0 0n 1n 1n 999n 2000n)\nV6 d1 0 PULSE(5 0 0 1n 1n 1999n 4000n)\nV7 d1b 0 PULSE(0 5 0 1n 1n 1999n 4000n)\nVDD Vref 0 DC 4 Version 4 SHEET 1 1884 680 WIRE -304 -464 -304 -480 WIRE -208 -416 -208 -448 WIRE -304 -368 -304 -384 WIRE -240 -368 -304 -368 WIRE -96 -368 -176 -368 WIRE -304 -352 -304 -368 WIRE -64 -352 -64 -448 WIRE -144 -304 -144 -448 WIRE -96 -304 -96 -368 WIRE 32 -304 -32 -304 WIRE -304 -256 -304 -272 WIRE -176 -256 -304 -256 WIRE -96 -256 -96 -304 WIRE -96 -256 -112 -256 WIRE -304 -240 -304 -256 WIRE 64 -240 64 -448 WIRE -208 -192 -208 -416 WIRE 32 -192 32 -304 WIRE 176 -192 96 -192 WIRE -304 -144 -304 -160 WIRE -240 -144 -304 -144 WIRE -96 -144 -176 -144 WIRE -16 -144 -16 -448 WIRE -304 -128 -304 -144 WIRE -96 -96 -96 -144 WIRE -48 -96 -96 -96 WIRE 32 -96 32 -192 WIRE 32 -96 16 -96 WIRE -144 -80 -144 -304 WIRE -304 -32 -304 -48 WIRE -176 -32 -304 -32 WIRE -96 -32 -96 -96 WIRE -96 -32 -112 -32 WIRE -304 -16 -304 -32 WIRE 176 16 176 -192 WIRE 240 16 176 16 WIRE 288 16 240 16 WIRE -208 32 -208 -192 WIRE 240 64 240 16 WIRE -304 80 -304 64 WIRE -240 80 -304 80 WIRE -96 80 -176 80 WIRE -64 80 -64 -352 WIRE -304 96 -304 80 WIRE -96 128 -96 80 WIRE 32 128 -32 128 WIRE -144 144 -144 -80 WIRE 240 160 240 128 WIRE -304 192 -304 176 WIRE -176 192 -304 192 WIRE -96 192 -96 128 WIRE -96 192 -112 192 WIRE 128 192 128 -448 WIRE -304 208 -304 192 WIRE 32 240 32 128 WIRE 96 240 32 240 WIRE 176 240 176 16 WIRE 176 240 160 240 WIRE -208 256 -208 32 WIRE -304 304 -304 288 WIRE -240 304 -304 304 WIRE -96 304 -176 304 WIRE -16 304 -16 -144 WIRE -304 320 -304 304 WIRE -96 352 -96 304 WIRE -48 352 -96 352 WIRE 32 352 32 240 WIRE 32 352 16 352 WIRE -144 368 -144 144 WIRE -304 416 -304 400 WIRE -176 416 -304 416 WIRE -96 416 -96 352 WIRE -96 416 -112 416 WIRE -304 432 -304 416 FLAG -304 432 0 FLAG -304 -480 VREF FLAG -208 -448 D0 FLAG -144 -448 D0b FLAG -64 -448 D1 FLAG -16 -448 D1b FLAG 64 -448 D2 FLAG 128 -448 D2b FLAG 288 16 Vout FLAG 240 160 0 SYMBOL Switch -144 416 M0 SYMATTR InstName X5 SYMBOL res -320 192 R0 SYMATTR InstName R1 SYMATTR Value 100 SYMBOL res -320 80 R0 SYMATTR InstName R2 SYMATTR Value 100 SYMBOL res -320 -32 R0 SYMATTR InstName R3 SYMATTR Value 100 SYMBOL res -320 -144 R0 SYMATTR InstName R4 SYMATTR Value 100 SYMBOL res -320 -256 R0 SYMATTR InstName R5 SYMATTR Value 100 SYMBOL res -320 -368 R0 SYMATTR InstName R6 SYMATTR Value 100 SYMBOL res -320 -480 R0 SYMATTR InstName R7 SYMATTR Value 100 SYMBOL res -320 304 R0 SYMATTR InstName R0 SYMATTR Value 100 SYMBOL Switch -144 192 M0 SYMATTR InstName X8 SYMBOL Switch -144 -32 M0 SYMATTR InstName X10 SYMBOL Switch -144 -256 M0 SYMATTR InstName X12 SYMBOL Switch -16 -96 M0 SYMATTR InstName X16 SYMBOL Switch -16 352 M0 SYMATTR InstName X17 SYMBOL Switch 64 -192 M0 SYMATTR InstName X18 SYMBOL cap 224 64 R0 SYMATTR InstName C1 SYMATTR Value 1p SYMBOL SwitchClosed 128 240 R0 SYMATTR InstName X1 SYMBOL SwitchClosed -64 -304 R0 SYMATTR InstName X2 SYMBOL SwitchClosed -64 128 R0 SYMATTR InstName X3 SYMBOL SwitchClosed -208 -368 R0 SYMATTR InstName X4 SYMBOL SwitchClosed -208 -144 R0 SYMATTR InstName X6 SYMBOL SwitchClosed -208 80 R0 SYMATTR InstName X7 SYMBOL SwitchClosed -208 304 R0 SYMATTR InstName X9 TEXT -352 -584 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1123u VT0=0.5 LAMBDA=0.018)\n.model CD4007P PMOS(LEVEL=1 KP=1123u VT0=-0.5 LAMBDA=0.018) TEXT 168 -504 Left 2 !.global VDD\n.include opamp.sub\nV4 d2b 0 PULSE(0 5 0 1n 1n 3999n 8000n)\nV1 d2 0 PULSE(5 0 0 1n 1n 3999n 8000n) TEXT 232 -144 Left 2 !.tran 18000n TEXT 160 -392 Left 2 !V2 d0b 0 PULSE(0 5 0 1n 1n 999n 2000n)\nV5 d0 0 PULSE(5 0 0n 1n 1n 999n 2000n)\nV6 d1 0 PULSE(5 0 0 1n 1n 1999n 4000n)\nV7 d1b 0 PULSE(0 5 0 1n 1n 1999n 4000n)\nVDD Vref 0 DC 4 |
At each resistance there is a LSB voltage difference.
D0b is the inverted signal of D0.
At certain code all "1" signals close the associated switches.
A voltage is transfered to Vout.
The shown circuit can be saved and simulated in LTSPICE giving a ramp test.
D0b is the inverted signal of D0.
At certain code all "1" signals close the associated switches.
A voltage is transfered to Vout.
The shown circuit can be saved and simulated in LTSPICE giving a ramp test.
3 Bit R string or ladder DAC
SpeedTime constant:Ideal voltage source at a series RC low pass. R = (3 R || 5 R) = 15/8 R Maximum resistance for half VDD, code 100... PowerStaticP_{RS} = \frac{V_{ref}^2}{R \cdot 2^{B}} Number of bitsResistance range:1 Ω .. 1 MΩ 20 bits. Resistance for MOSFET switches and contacts. Complexity2B resistors and 2 * 2B switches are a high element count |
Version 4 SHEET 1 1884 680 WIRE -304 -464 -304 -480 WIRE -208 -416 -208 -448 WIRE -304 -368 -304 -384 WIRE -240 -368 -304 -368 WIRE -96 -368 -176 -368 WIRE -304 -352 -304 -368 WIRE -64 -352 -64 -448 WIRE -144 -304 -144 -448 WIRE -96 -304 -96 -368 WIRE 32 -304 -32 -304 WIRE -304 -256 -304 -272 WIRE -176 -256 -304 -256 WIRE -96 -256 -96 -304 WIRE -96 -256 -112 -256 WIRE -304 -240 -304 -256 WIRE 64 -240 64 -448 WIRE -208 -192 -208 -416 WIRE 32 -192 32 -304 WIRE 176 -192 96 -192 WIRE -304 -144 -304 -160 WIRE -240 -144 -304 -144 WIRE -96 -144 -176 -144 WIRE -16 -144 -16 -448 WIRE -304 -128 -304 -144 WIRE -96 -96 -96 -144 WIRE -48 -96 -96 -96 WIRE 32 -96 32 -192 WIRE 32 -96 16 -96 WIRE -144 -80 -144 -304 WIRE -304 -32 -304 -48 WIRE -176 -32 -304 -32 WIRE -96 -32 -96 -96 WIRE -96 -32 -112 -32 WIRE -304 -16 -304 -32 WIRE 176 16 176 -192 WIRE 240 16 176 16 WIRE 288 16 240 16 WIRE -208 32 -208 -192 WIRE 240 64 240 16 WIRE -304 80 -304 64 WIRE -240 80 -304 80 WIRE -96 80 -176 80 WIRE -64 80 -64 -352 WIRE -304 96 -304 80 WIRE -96 128 -96 80 WIRE 32 128 -32 128 WIRE -144 144 -144 -80 WIRE 240 160 240 128 WIRE -304 192 -304 176 WIRE -176 192 -304 192 WIRE -96 192 -96 128 WIRE -96 192 -112 192 WIRE 128 192 128 -448 WIRE -304 208 -304 192 WIRE 32 240 32 128 WIRE 96 240 32 240 WIRE 176 240 176 16 WIRE 176 240 160 240 WIRE -208 256 -208 32 WIRE -304 304 -304 288 WIRE -240 304 -304 304 WIRE -96 304 -176 304 WIRE -16 304 -16 -144 WIRE -304 320 -304 304 WIRE -96 352 -96 304 WIRE -48 352 -96 352 WIRE 32 352 32 240 WIRE 32 352 16 352 WIRE -144 368 -144 144 WIRE -304 416 -304 400 WIRE -176 416 -304 416 WIRE -96 416 -96 352 WIRE -96 416 -112 416 WIRE -304 432 -304 416 FLAG -304 432 0 FLAG -304 -480 VREF FLAG -208 -448 D0 FLAG -144 -448 D0b FLAG -64 -448 D1 FLAG -16 -448 D1b FLAG 64 -448 D2 FLAG 128 -448 D2b FLAG 288 16 Vout FLAG 240 160 0 SYMBOL Switch -144 416 M0 SYMATTR InstName X5 SYMBOL res -320 192 R0 SYMATTR InstName R1 SYMATTR Value 100 SYMBOL res -320 80 R0 SYMATTR InstName R2 SYMATTR Value 100 SYMBOL res -320 -32 R0 SYMATTR InstName R3 SYMATTR Value 100 SYMBOL res -320 -144 R0 SYMATTR InstName R4 SYMATTR Value 100 SYMBOL res -320 -256 R0 SYMATTR InstName R5 SYMATTR Value 100 SYMBOL res -320 -368 R0 SYMATTR InstName R6 SYMATTR Value 100 SYMBOL res -320 -480 R0 SYMATTR InstName R7 SYMATTR Value 100 SYMBOL res -320 304 R0 SYMATTR InstName R0 SYMATTR Value 100 SYMBOL Switch -208 304 M0 SYMATTR InstName X7 SYMBOL Switch -144 192 M0 SYMATTR InstName X8 SYMBOL Switch -208 80 M0 SYMATTR InstName X9 SYMBOL Switch -144 -32 M0 SYMATTR InstName X10 SYMBOL Switch -208 -144 M0 SYMATTR InstName X11 SYMBOL Switch -144 -256 M0 SYMATTR InstName X12 SYMBOL Switch -208 -368 M0 SYMATTR InstName X13 SYMBOL Switch -64 128 M0 SYMATTR InstName X14 SYMBOL Switch -64 -304 M0 SYMATTR InstName X15 SYMBOL Switch -16 -96 M0 SYMATTR InstName X16 SYMBOL Switch -16 352 M0 SYMATTR InstName X17 SYMBOL Switch 64 -192 M0 SYMATTR InstName X18 SYMBOL Switch 128 240 M0 SYMATTR InstName X19 SYMBOL cap 224 64 R0 SYMATTR InstName C1 SYMATTR Value 1p TEXT -352 -584 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1123u VT0=0.5 LAMBDA=0.018)\n.model CD4007P PMOS(LEVEL=1 KP=1123u VT0=-0.5 LAMBDA=0.018) TEXT 168 -504 Left 2 !.global VDD\n.include opamp.sub\nV4 d2b 0 PULSE(0 5 0 1n 1n 3999n 8000n)\nV1 d2 0 PULSE(5 0 0 1n 1n 3999n 8000n) TEXT 232 -144 Left 2 !.tran 18000n TEXT 160 -392 Left 2 !V2 d0b 0 PULSE(0 5 0 1n 1n 999n 2000n)\nV5 d0 0 PULSE(5 0 0n 1n 1n 999n 2000n)\nV6 d1 0 PULSE(5 0 0 1n 1n 1999n 4000n)\nV7 d1b 0 PULSE(0 5 0 1n 1n 1999n 4000n)\nVDD Vref 0 DC 4 |
τ = 0.25 · 2B R C
There are 2B of unit resistors.
The highest resistance is at midpoint. Half resistance will be connected to VDD and half to ground.
For equivalent resistance these resistances are in parallel.
There are 2B of unit resistors.
The highest resistance is at midpoint. Half resistance will be connected to VDD and half to ground.
For equivalent resistance these resistances are in parallel.
Practical example
M. Pelgrom, “A 10-b 50-MHz CMOS D/A Converter with 75-W Buffer,” JSSC, Dec. 1990, pp. 1347
1 V pp output into 75 Ω, 25 pF load
1.6 µm CMOS, 5 V; 65mW (50 MHz, 1Vpp); 1024 resistors 6..10 Ω
16 large resistors 250 Ω parallel to 32 75 Ω polysilison resistors with switches each;
Power: driver transistor 7.3 mA, driver circuit 4 mA; ladder current 1mA, digital 0.7 mA: total 13mA.
Rise fall time 6ns; 19 Mhz signal bandwidth; 50 MHz sample frequency; 2.5 mm2 die size
DNL; INL < 0.35; 5MHz Signal -53 dB to total harmonic distortion
Resolution: 8, 14, 20 bit
Frequency: 10 kHz, 1 MHz, 100 MHz
VDD = VREF = 1V (Integrated Circuits)
Cload = 10 pF (oscilloscope)
4 Bit interpolating R string, ladder DAC
Version 4 SHEET 1 1884 680 WIRE -608 -32 -640 -32 WIRE -528 -16 -544 -16 WIRE -480 -16 -528 -16 WIRE -320 -16 -320 -64 WIRE -608 0 -624 0 WIRE -928 32 -928 0 WIRE -800 32 -928 32 WIRE -672 32 -736 32 WIRE -624 32 -624 0 WIRE -528 32 -528 -16 WIRE -528 32 -624 32 WIRE -480 32 -480 -16 WIRE -352 32 -480 32 WIRE -272 32 -288 32 WIRE -256 32 -272 32 WIRE -96 32 -192 32 WIRE -928 48 -928 32 WIRE -480 48 -480 32 WIRE -384 96 -384 -64 WIRE -928 144 -928 128 WIRE -864 144 -928 144 WIRE -640 144 -640 -32 WIRE -640 144 -800 144 WIRE -480 144 -480 128 WIRE -416 144 -480 144 WIRE -272 144 -272 32 WIRE -272 144 -352 144 WIRE -928 160 -928 144 WIRE -480 160 -480 144 WIRE -96 192 -96 32 WIRE -48 192 -96 192 WIRE -320 208 -320 -16 WIRE -144 208 -144 192 WIRE -928 256 -928 240 WIRE -800 256 -928 256 WIRE -672 256 -672 32 WIRE -672 256 -736 256 WIRE -480 256 -480 240 WIRE -352 256 -480 256 WIRE -176 256 -288 256 WIRE -96 256 -96 192 WIRE -96 256 -112 256 WIRE -928 272 -928 256 WIRE -480 272 -480 256 WIRE -384 320 -384 96 WIRE -928 368 -928 352 WIRE -864 368 -928 368 WIRE -640 368 -640 144 WIRE -640 368 -800 368 WIRE -480 368 -480 352 WIRE -416 368 -480 368 WIRE -272 368 -352 368 WIRE -192 368 -192 352 WIRE -928 384 -928 368 WIRE -480 384 -480 368 WIRE -272 416 -272 368 WIRE -224 416 -272 416 WIRE -96 416 -96 256 WIRE -96 416 -160 416 WIRE -320 432 -320 208 WIRE -928 480 -928 464 WIRE -800 480 -928 480 WIRE -672 480 -672 256 WIRE -672 480 -736 480 WIRE -640 480 -672 480 WIRE -480 480 -480 464 WIRE -352 480 -480 480 WIRE -272 480 -272 416 WIRE -272 480 -288 480 WIRE -928 496 -928 480 WIRE -560 496 -576 496 WIRE -512 496 -560 496 WIRE -480 496 -480 480 WIRE -480 496 -512 496 WIRE -640 512 -656 512 WIRE -656 544 -656 512 WIRE -560 544 -560 496 WIRE -560 544 -656 544 FLAG -928 496 0 FLAG -928 0 VREF FLAG -768 -16 D3 FLAG -832 96 D3b FLAG -768 208 D23 FLAG -832 320 D2b FLAG -768 432 D2 FLAG -48 192 Vout FLAG -480 -16 VB FLAG -512 496 VA FLAG -384 -64 D0 FLAG -320 -64 D0b FLAG -192 352 D1 FLAG -144 192 D01 FLAG -224 -16 D1b SYMBOL Switch -320 480 M0 SYMATTR InstName X7 SYMBOL res -496 256 R0 SYMATTR InstName R1 SYMATTR Value 100 SYMBOL res -496 144 R0 SYMATTR InstName R2 SYMATTR Value 100 SYMBOL res -496 32 R0 SYMATTR InstName R3 SYMATTR Value 100 SYMBOL res -496 368 R0 SYMATTR InstName R8 SYMATTR Value 100 SYMBOL Switch -384 368 M0 SYMATTR InstName X8 SYMBOL Switch -320 256 M0 SYMATTR InstName X9 SYMBOL Switch -384 144 M0 SYMATTR InstName X10 SYMBOL Switch -768 480 M0 SYMATTR InstName X15 SYMBOL res -944 256 R0 SYMATTR InstName R9 SYMATTR Value 100 SYMBOL res -944 144 R0 SYMATTR InstName R10 SYMATTR Value 100 SYMBOL res -944 32 R0 SYMATTR InstName R11 SYMATTR Value 100 SYMBOL res -944 368 R0 SYMATTR InstName R16 SYMATTR Value 100 SYMBOL Switch -832 368 M0 SYMATTR InstName X16 SYMBOL Switch -768 256 M0 SYMATTR InstName X17 SYMBOL Switch -832 144 M0 SYMATTR InstName X18 SYMBOL Switch -768 32 M0 SYMATTR InstName X19 SYMBOL Opamps\\opamp -576 48 M180 SYMATTR InstName U2 SYMBOL Opamps\\opamp -608 560 M180 SYMATTR InstName U3 SYMBOL Switch -192 416 M0 SYMATTR InstName X12 SYMBOL Switch -144 256 M0 SYMATTR InstName X13 SYMBOL Switch -224 32 M0 SYMATTR InstName X14 SYMBOL Switch -320 32 M0 SYMATTR InstName X1 TEXT -664 -312 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1123u VT0=0.5 LAMBDA=0.018)\n.model CD4007P PMOS(LEVEL=1 KP=1123u VT0=-0.5 LAMBDA=0.018) TEXT -952 -264 Left 2 !.global VDD\n.include opamp.sub\nV0 d3 0 PULSE(-1 5 6000n 1n 1n 1999n 8000n)\nV1 d3b 0 PULSE(-1 5 4000n 1n 1n 3999n 8000n)\nV2 d23 0 PULSE(-1 5 2000n 1n 1n 3999n 8000n)\nV3 d2b 0 PULSE(-1 5 0n 1n 1n 3999n 8000n)\nV4 d2 0 PULSE(-1 5 0n 1n 1n 1999n 8000n) TEXT -896 -64 Left 2 !.tran 18000n TEXT -184 -232 Left 2 !V5 d1 0 PULSE(5 -1 999n 1n 1n 2499n 4000n)\nV6 d1b 0 PULSE(-1 5 1499n 1n 1n 1499n 4000n)\nV7 d0b 0 PULSE(-1 5 0n 1n 1n 499n 1000n)\nV8 d0 0 PULSE(5 -1 0n 1n 1n 499n 1000n)\nV9 d01 0 PULSE(-1 5 999n 1n 1n 499n 2000n)\nVref Vref 0 DC 4\nVDD VDD 0 DC 4 |
|
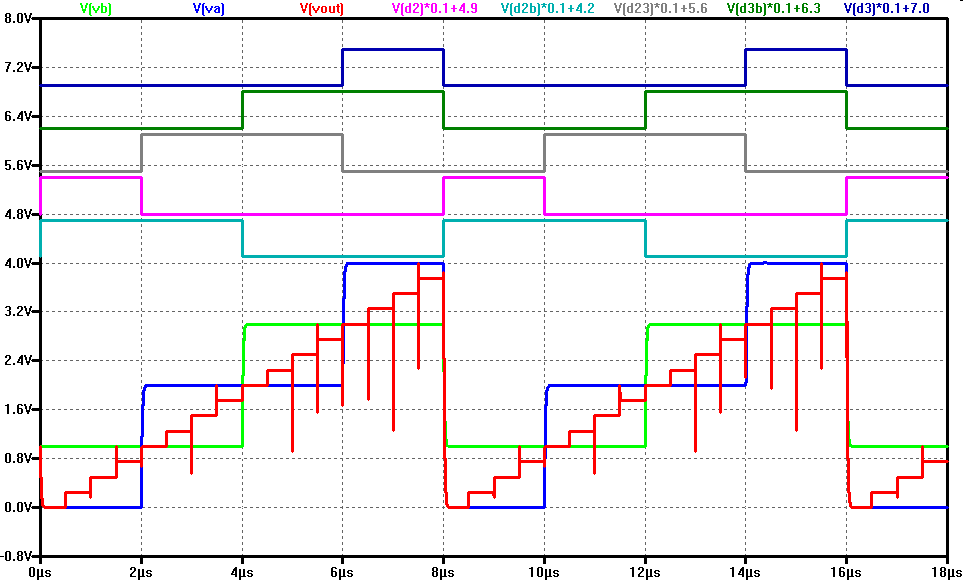
Extra logic is needed to generate the control signals from the binary input code.
2 switches are always active on the left side for the 2 high order bits providing an upper and lower voltage for interpolation.
The simulation shows the control signals for the upper bits, the intermediate voltages VA and VB and the resulting output voltage Vout.
2 switches are always active on the left side for the 2 high order bits providing an upper and lower voltage for interpolation.
The simulation shows the control signals for the upper bits, the intermediate voltages VA and VB and the resulting output voltage Vout.
| MSB DA3 | DA2 | DA1 | LSB DA0 |
D3 | D3b | D23 | D2b | D2 | D1 | D1b | D01 | D0 | D0B | VA/V | VB/V |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
3 Bit binary charge scaling DAC
|
Each capacitor is binary weighted. V_{max} = V_{ref} Using equivalent current sources: \underline{I}_{Di} = \underline{V}_{ref} \cdot j ω C_{i} V(D2D1D0)= V_{ref} \frac{D2 \cdot C_{2} + D1 \cdot C_{1} + D0 \cdot C_{0} }{C_{Total}} C_{Total} = \sum_{i=0}^N C_{i} |
Version 4 SHEET 1 1884 680 WIRE 288 -96 192 -96 WIRE 400 -96 288 -96 WIRE 512 -96 400 -96 WIRE 608 -96 512 -96 WIRE 656 -96 608 -96 WIRE 288 -80 288 -96 WIRE 400 -80 400 -96 WIRE 512 -80 512 -96 WIRE 736 -80 720 -80 WIRE 784 -80 736 -80 WIRE 192 -64 192 -96 WIRE 656 -64 640 -64 WIRE 640 -32 640 -64 WIRE 736 -32 736 -80 WIRE 736 -32 640 -32 WIRE 272 80 272 64 WIRE 384 80 384 64 WIRE 384 80 272 80 WIRE 496 80 496 64 WIRE 496 80 384 80 WIRE 640 80 496 80 WIRE 192 96 192 0 WIRE 304 96 304 64 WIRE 304 96 192 96 WIRE 416 96 416 64 WIRE 416 96 304 96 WIRE 528 96 528 64 WIRE 528 96 416 96 WIRE 640 96 528 96 WIRE 256 112 256 32 WIRE 368 112 368 32 WIRE 480 112 480 32 WIRE 640 112 640 96 FLAG 784 -80 Vout IOPIN 784 -80 Out FLAG 144 -32 reset IOPIN 144 -32 In FLAG 640 80 Vref IOPIN 640 80 In FLAG 640 112 0 FLAG 480 112 D0 IOPIN 480 112 In FLAG 368 112 D1 IOPIN 368 112 In FLAG 256 112 D2 IOPIN 256 112 In FLAG 608 -96 Vint SYMBOL Opamps\\opamp 688 -16 M180 SYMATTR InstName U1 SYMBOL cap 496 -80 R0 SYMATTR InstName C0 SYMATTR Value 1� SYMBOL cap 384 -80 R0 SYMATTR InstName C1 SYMATTR Value 2� SYMBOL cap 272 -80 R0 SYMATTR InstName C2 SYMATTR Value 4� SYMBOL Switch2 288 32 R270 SYMATTR InstName X1 SYMBOL Switch2 400 32 R270 SYMATTR InstName X2 SYMBOL Switch2 512 32 R270 SYMATTR InstName X3 SYMBOL Switch 192 -32 R270 SYMATTR InstName X4 |
Therefore reset switches are needed after each cycle.
Alternatively a code of all 0 can be applied between data output.
This causes additional power consumption.
4 Bit binary split array charge DAC
|
The range of C can be limited using a coupling capacitor C4. |
Version 4 SHEET 1 1884 680 WIRE 144 -96 80 -96 WIRE 288 -96 144 -96 WIRE 400 -96 288 -96 WIRE 432 -96 400 -96 WIRE 512 -96 496 -96 WIRE 592 -96 512 -96 WIRE 688 -96 592 -96 WIRE 736 -96 688 -96 WIRE 144 -80 144 -96 WIRE 288 -80 288 -96 WIRE 400 -80 400 -96 WIRE 512 -80 512 -96 WIRE 592 -80 592 -96 WIRE 816 -80 800 -80 WIRE 864 -80 816 -80 WIRE 736 -64 720 -64 WIRE 720 -32 720 -64 WIRE 816 -32 816 -80 WIRE 816 -32 720 -32 WIRE 80 -16 80 -96 WIRE 688 -16 688 -96 WIRE 768 16 736 16 WIRE 272 80 272 64 WIRE 384 80 384 64 WIRE 384 80 272 80 WIRE 496 80 496 64 WIRE 496 80 384 80 WIRE 576 80 576 64 WIRE 576 80 496 80 WIRE 720 80 576 80 WIRE 80 96 80 48 WIRE 144 96 144 -16 WIRE 144 96 80 96 WIRE 304 96 304 64 WIRE 304 96 144 96 WIRE 416 96 416 64 WIRE 416 96 304 96 WIRE 528 96 528 64 WIRE 528 96 416 96 WIRE 608 96 608 64 WIRE 608 96 528 96 WIRE 688 96 688 48 WIRE 688 96 608 96 WIRE 720 96 688 96 WIRE 256 112 256 32 WIRE 368 112 368 32 WIRE 480 112 480 32 WIRE 560 112 560 32 WIRE 720 112 720 96 FLAG 864 -80 Vout IOPIN 864 -80 Out FLAG 32 16 reset IOPIN 32 16 In FLAG 720 80 Vref IOPIN 720 80 In FLAG 720 112 0 FLAG 480 112 D2 IOPIN 480 112 In FLAG 368 112 D1 IOPIN 368 112 In FLAG 256 112 D0 IOPIN 256 112 In FLAG 688 -96 Vint FLAG 768 16 reset IOPIN 768 16 In FLAG 560 112 D3 IOPIN 560 112 In SYMBOL Opamps\\opamp 768 -16 M180 SYMATTR InstName U1 SYMBOL cap 496 -80 R0 SYMATTR InstName C2 SYMATTR Value 100n SYMBOL cap 384 -80 R0 SYMATTR InstName C1 SYMATTR Value 200n SYMBOL cap 272 -80 R0 SYMATTR InstName C0 SYMATTR Value 100n SYMBOL Switch2 288 32 R270 SYMATTR InstName X1 SYMBOL Switch2 400 32 R270 SYMATTR InstName X2 SYMBOL Switch2 512 32 R270 SYMATTR InstName X3 SYMBOL cap 496 -112 R90 WINDOW 0 0 32 VBottom 2 WINDOW 3 32 32 VTop 2 SYMATTR InstName C5 SYMATTR Value 100n SYMBOL Switch 688 16 R90 SYMATTR InstName X4 SYMBOL Switch 80 16 M90 SYMATTR InstName X5 SYMBOL cap 576 -80 R0 SYMATTR InstName C3 SYMATTR Value 200n SYMBOL Switch2 592 32 R270 SYMATTR InstName X6 SYMBOL cap 128 -80 R0 SYMATTR InstName C6 SYMATTR Value 100n TEXT 48 -176 Left 2 !.model CD4007N NMOS(LEVEL=1 KP=1123u VT0=0.5 LAMBDA=0.018)\n.model CD4007P PMOS(LEVEL=1 KP=1123u VT0=-0.5 LAMBDA=0.018) TEXT -32 128 Left 2 !.global VDD\n.include opamp.sub\nV0 reset 0 PULSE(-1 5 0 1n 1n 499n 16000n)\nV4 d3 0 PULSE(5 -1 0 1n 1n 7999n 16000n)\nV1 d2 0 PULSE(5 -1 0 1n 1n 3999n 8000n) TEXT 776 -136 Left 2 !.tran 18000n TEXT 456 184 Left 2 !V2 d1 0 PULSE(5 -1 0 1n 1n 1999n 4000n)\nV3 d0 0 PULSE(5 -1 0n 1n 1n 999n 2000n)\nVref Vref 0 DC 4\nVDD VDD DC 4 |
R2R DAC
|
Only R and 2R values are needed. |
Version 4 SHEET 1 1212 680 WIRE -48 -480 -128 -480 WIRE -528 -384 -592 -384 WIRE -496 -384 -528 -384 WIRE -480 -384 -496 -384 WIRE -384 -384 -400 -384 WIRE -368 -384 -384 -384 WIRE -272 -384 -288 -384 WIRE -256 -384 -272 -384 WIRE -160 -384 -176 -384 WIRE -128 -384 -128 -480 WIRE -128 -384 -160 -384 WIRE -96 -384 -128 -384 WIRE 16 -384 -16 -384 WIRE 16 -368 16 -384 WIRE -496 -352 -496 -384 WIRE -384 -352 -384 -384 WIRE -272 -352 -272 -384 WIRE -160 -352 -160 -384 WIRE -592 -336 -592 -384 WIRE 16 -272 16 -304 WIRE -496 -240 -496 -272 WIRE -384 -240 -384 -272 WIRE -272 -240 -272 -272 WIRE -160 -240 -160 -272 WIRE -592 -208 -592 -256 FLAG -592 -208 0 FLAG -496 -240 D0 IOPIN -496 -240 In FLAG 16 -272 0 FLAG 16 -384 Voutfx FLAG -384 -240 D1 IOPIN -384 -240 In FLAG -272 -240 D2 IOPIN -272 -240 In FLAG -160 -240 D3 IOPIN -160 -240 In FLAG -48 -480 Vout IOPIN -48 -480 Out FLAG -528 -384 V0L FLAG -384 -384 V1L FLAG -272 -384 V2L SYMBOL res -608 -352 R0 SYMATTR InstName R0 SYMATTR Value 2k SYMBOL res -512 -368 R0 SYMATTR InstName R1 SYMATTR Value 2k SYMBOL res -496 -368 R270 WINDOW 0 32 56 VTop 2 WINDOW 3 0 56 VBottom 2 SYMATTR InstName R5 SYMATTR Value 1k SYMBOL res 0 -400 R90 WINDOW 0 0 56 VBottom 2 WINDOW 3 32 56 VTop 2 SYMATTR InstName R8 SYMATTR Value 10k SYMBOL cap 0 -368 R0 SYMATTR InstName C2 SYMATTR Value 1p SYMBOL res -400 -368 R0 SYMATTR InstName R2 SYMATTR Value 2k SYMBOL res -384 -368 R270 WINDOW 0 32 56 VTop 2 WINDOW 3 0 56 VBottom 2 SYMATTR InstName R6 SYMATTR Value 1k SYMBOL res -288 -368 R0 SYMATTR InstName R3 SYMATTR Value 2k SYMBOL res -160 -368 M270 WINDOW 0 32 56 VTop 2 WINDOW 3 0 56 VBottom 2 SYMATTR InstName R7 SYMATTR Value 1k SYMBOL res -176 -368 R0 SYMATTR InstName R4 SYMATTR Value 2k TEXT -392 -168 Left 2 !VD0 D0 0 PULSE(1 0 0 1n 1n 99n 200n)\nVD1 D1 0 PULSE(1 0 0 1n 1n 199n 400n)\nVD2 D2 0 PULSE(1 0 0 1n 1n 399n 800n)\nVD3 D3 0 PULSE(1 0 0 1n 1n 799n 1600n) TEXT -608 -160 Left 2 !.tran 2u |
Calculation of output voltage with equivalent sources:
R is 1 kΩ.
All data inputs can be looked at as voltage sources VD0...VD3.
The voltages internally for equivalent sources are V0L..V2L, VoutL.
V_{0L} = V_{D0} \frac{2 R}{4 R} = V_{D0} \frac{1}{2}
R_{i0} = 2 R || 2R = \frac{2 R 2 R}{2 R + 2 R} = R
V_{1L} = (V_{0L} - V_{D1}) \frac{2 R}{4 R} + V_{D1} = V_{0L} \frac{1}{2} + V_{D1} \frac{1}{2} = V_{D0} \frac{1}{4} + V_{D1} \frac{1}{2}
R_{i1} = 2 R || 2R = \frac{2 R 2 R}{2 R + 2 R} = R
V_{nL} = (V_{(n-1)L} - V_{Dn}) \frac{2 R}{4 R} + V_{Dn} = V_{(n-1)L} \frac{1}{2} + V_{Dn} \frac{1}{2} = \sum_{i=0}^{n} \frac{V_{Di}}{2^{n-i+1}}
Capacitors can be used instead of the resistance R giving a C2C DAC.
R is 1 kΩ.
All data inputs can be looked at as voltage sources VD0...VD3.
The voltages internally for equivalent sources are V0L..V2L, VoutL.
V_{0L} = V_{D0} \frac{2 R}{4 R} = V_{D0} \frac{1}{2}
R_{i0} = 2 R || 2R = \frac{2 R 2 R}{2 R + 2 R} = R
V_{1L} = (V_{0L} - V_{D1}) \frac{2 R}{4 R} + V_{D1} = V_{0L} \frac{1}{2} + V_{D1} \frac{1}{2} = V_{D0} \frac{1}{4} + V_{D1} \frac{1}{2}
R_{i1} = 2 R || 2R = \frac{2 R 2 R}{2 R + 2 R} = R
V_{nL} = (V_{(n-1)L} - V_{Dn}) \frac{2 R}{4 R} + V_{Dn} = V_{(n-1)L} \frac{1}{2} + V_{Dn} \frac{1}{2} = \sum_{i=0}^{n} \frac{V_{Di}}{2^{n-i+1}}
Capacitors can be used instead of the resistance R giving a C2C DAC.
Practical considerations
|
Variations of components: R, C, V offset of operational amplifier What is allowed to have less than 1/2 LSB INL and DNL? |
Low Cost Serial C DAC Circuit
|
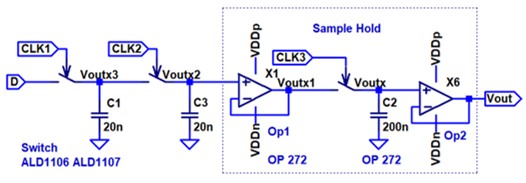
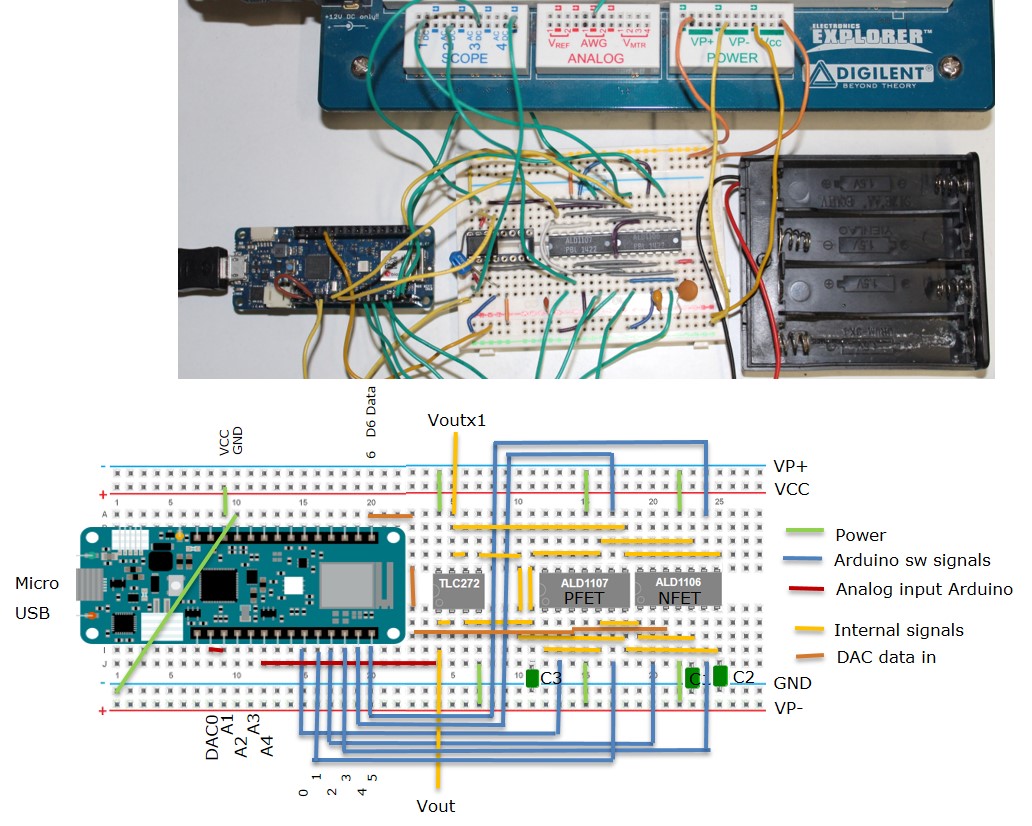
Simulation schematic LTSPICE Minimum number of parts Number of cycles gives the resolution Low cost Arduino MKR WIFI1010 TLC272 ALD1106, ALD1107 3x C=20nF Breadboard Study DAC simulation, measurement, errors and error correction |
  |
Voutx2(n+1) = \frac{Voutx2(n) + Voutx3}{2}
= \frac{Voutx2(n) + VDD \cdot D(n)}{2}
Voutx2(n+1) = VDD \cdot (0.25 \cdot Voutx2(n-1) + 0.25 \cdot D(n-1) + 0.5 \cdot D(n)
Vout = \sum_{k=0}^{nBit-1} 2^{-nBit+k} D(k)
Vollrath, "Low cost serial DAC", MPC Workshop, 2024
Voutx2(n+1) = VDD \cdot (0.25 \cdot Voutx2(n-1) + 0.25 \cdot D(n-1) + 0.5 \cdot D(n)
Vout = \sum_{k=0}^{nBit-1} 2^{-nBit+k} D(k)
Vollrath, "Low cost serial DAC", MPC Workshop, 2024
References
C. Lin and K. Buit, " A 10-b, 500- MSample/s CMOS DAC in 0.6mm2", JSSC, vol. 33, pp.1948-1958,1998Untrimmed segmented
T. Miki et al, “An 80-MHz 8-bit CMOS D/A Converter,” JSSC December 1986, pp. 983
A. Van den Bosch et al, “A 1-GSample/s Nyquist Current-Steering CMOS D/A Converter,” JSSC March 2001, pp. 315 Savoj, J, A 12-GS/s Phase-Calibrated CMOS Digital-to-Analog Converter for Backplane Communications , JSSC, 2008, pp. 1207 - 1216
Current copiers:
D. W. J. Groeneveld et al, “A Self-Calibration Technique for Monolithic High-Resolution D/A Converters,” JSSC December 1989, pp. 1517
Dynamic element matching:
R. J. van de Plassche, “Dynamic Element Matching for High-Accuracy Monolithic D/A Converters,” JSSC December 1976, pp. 795