Hochschule Kempten      
Fakultät Elektrotechnik      
Interface Electronics       Fachgebiet Elektronik, Prof. Vollrath      

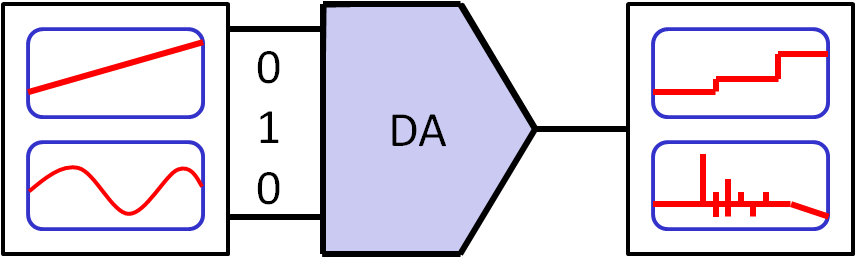
Interface Electronics

07 DAC practical considerations

Prof. Dr. Jörg Vollrath


06 DAC errors


Video Lecture: DAC practical considerations


Länge: 01:06:27
0:0:0 Interface Electronics

0:0:10 Ideal INL, DNL

0:0:42 DAC calibration example

0:3:3 Resistors and capacitances

0:5:35 Errors and resistance

0:6:53 DAC settling time Full scale, mid scale

0:11:29 DAC timing glitch

0:13:23 Sampling sine signal

0:15:8 DAC spectral measurement

0:18:20 DAC FFT with to many samples

0:24:17 One value per output code

0:25:3 DAC tool chain

0:26:4 DAC Evolution comparison

0:32:55 WS2012 Problem 4

0:38:11 Settling time

0:42:27 t > R C (B+1) ln(2) = 30 ns

0:46:0 Output voltage

0:48:51 Vout = (VD2/R3+VD1/R2+VD0/R1)Rout

0:54:34 Code = 001

Review and Overview

DAC settling time

  • Data Conversion Handbook p.292
  • Full scale settling time: 000...111
    • Linear Technolgy (AN120f)
    • Analog Devices MT-013
  • Mid scale settling time: 011..100
    • Analog Devices MT-013

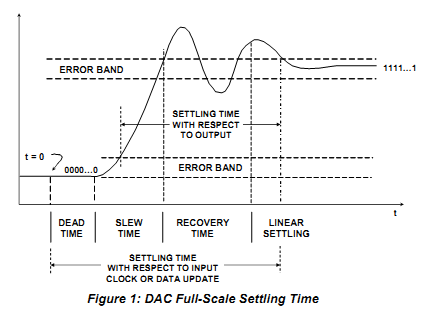
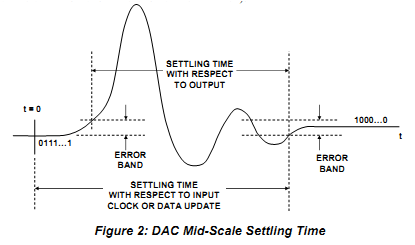
DAC timing glitch

  • Consider mid scale transition:
    011..100
  • Full scale settling time: 000...111
  • Output depends on timing between LSB and MSB
    • Ideal
    • Late MSB
    • Early MSB
Application of a sample and hold.

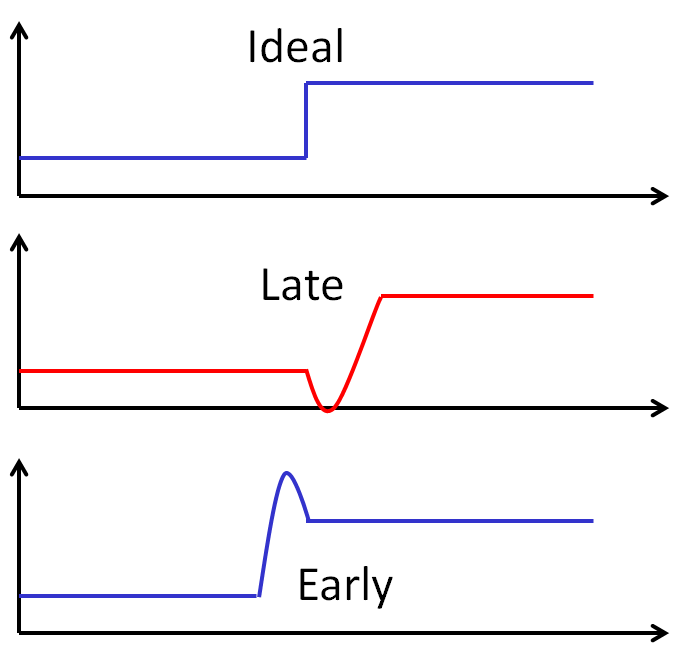
Sampling a sine signal

  • Sine signal (screen: 500x500 points)
    Looks smooth good
  • Zoom:
  • DAC signal generation
    Code has fixed sampling time and leads to steps > 1 LSB
  • Oscilloscope has a fixed high sampling rate
    FFT only with filtered useful values
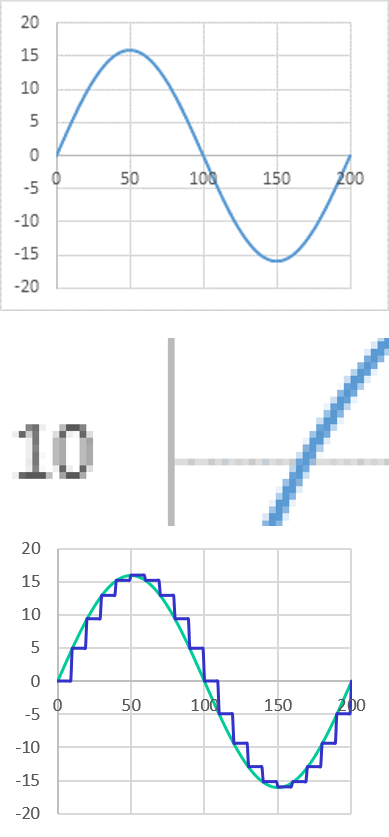
A sine function is generated with a x step size of 5.
The output looks like a low bit quantization despite using a very precise floating point number.
The y step size is very big for each step, but can vary a lot.

DAC spectral measurement

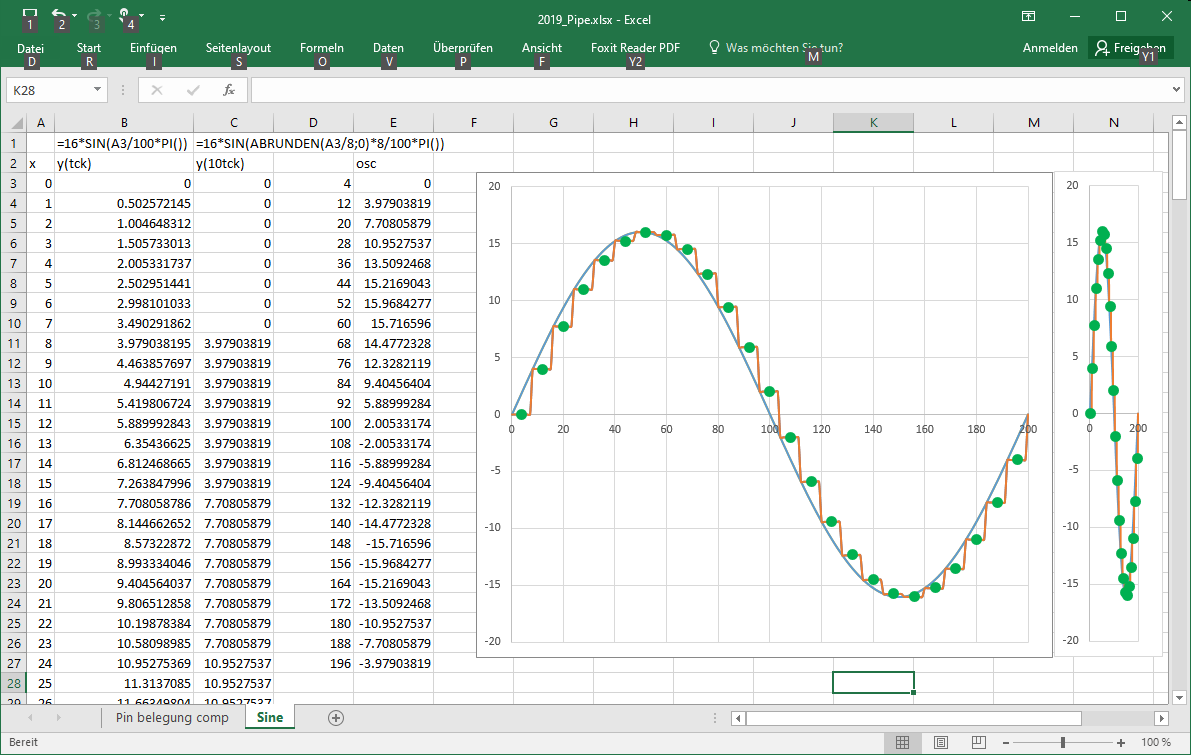
Just sampling in Excel gives a kind of quantization.

DAC spectral measurement

  • Red dots ideal measurement
  • One sample per output code after settling time
  • Measurement with higher sample rate
  • All samples, steps create harmonics
  • Overshoot, undershoot?
  • Measurement early during settling time
FFT results

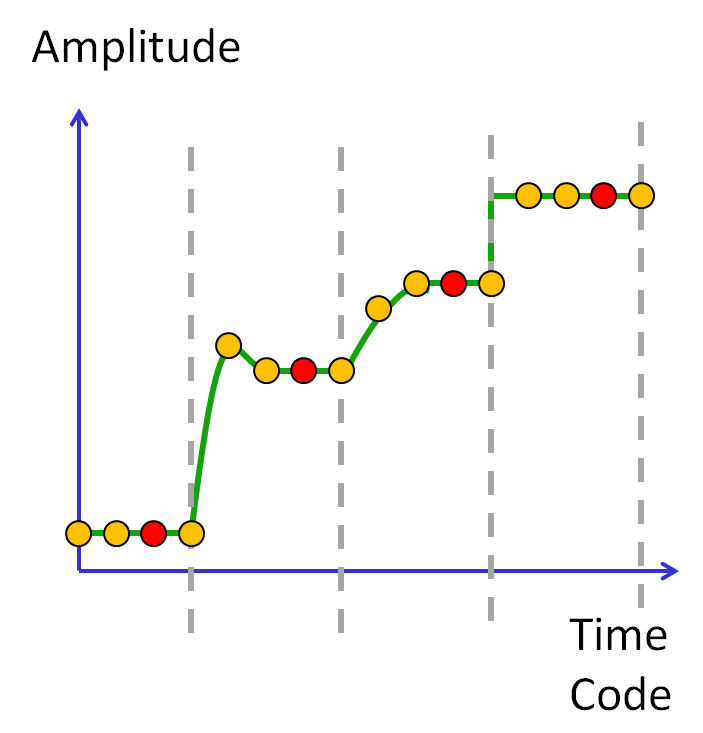
DAC distortion measurement

Sine signal and FFT
10 bit, 11 periods, 2048 points, 16 samples per point


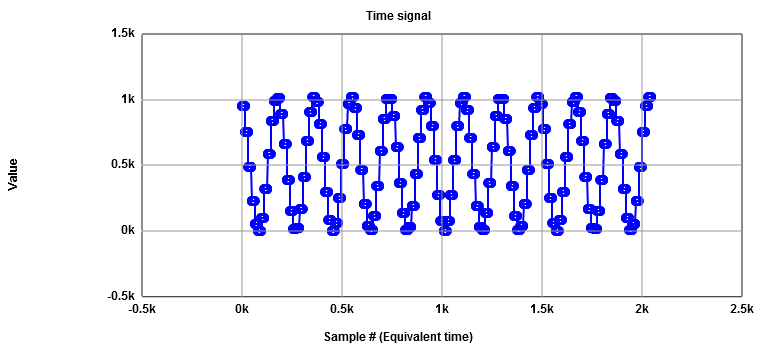
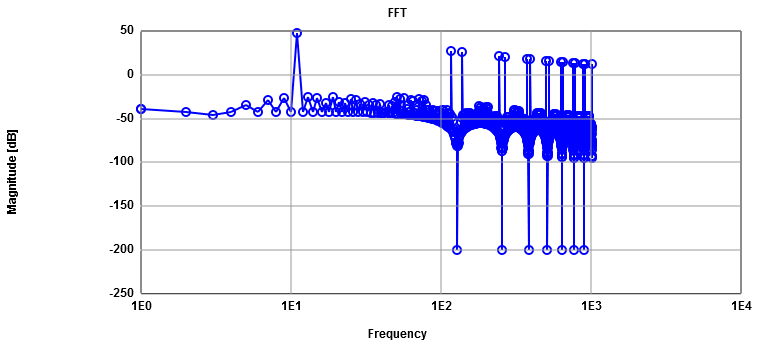
Signal (11) 48 dB, total noise 31 dB (ideal simulation -10 dB)
Harmonics () 27 dB..12 dB
Noise floor peaks -26 dB, total noise -14 dB
You can not estimate levels looking at the graph with reasonable accuracy.
Numerical calculation is required.
10 log (N/2) = 30 dB
Excel:
x, column A: 0..2047 points
y, column B: = RUNDEN(511.5 + 511.5 * SIN(RUNDEN(A2 / 16;0) * 16/2048*11*2*PI());0)
Javascript:
Math.round(offset + amplitude * Math.sin( Math.round(i/nStep) * nStep / nPoints * nPeriods * 2 *Math.PI()))

Javascript FFT

DAC full system

Reconstruction filters:
  • Digital filter
    • Band limit
    • pre-emphasis to compensate for droop
  • DAC
  • Low pass filter
    • switched capacitor and continuous time filter

DAC evolution comparison

198620012008
Data Rate80 MHz1GS/s12GS/s
Resolution8 bit (6+2)10bit(5+5)8bit(5+3)
Technology2 µm0.35 µm90nm
Scaling factor15.722
Supply voltage5V3V/1.9V1.8V/1V
Area3.7mm20.35mm20.23mm2
Ratio expected/real1/132/10512/18
Power145mW110mW190mW

Untrimmed segmented DACs:
T. Miki et al, “An 80-MHz 8-bit CMOS D/A Converter,” JSSC December 1986, pp. 983
A. Van den Bosch et al, “A 1-GSample/s Nyquist Current-Steering CMOS D/A Converter,” JSSC March 2001, pp. 315
Savoj, J, A 12-GS/s Phase-Calibrated CMOS Digital-to-Analog Converter for Backplane Communications , JSSC, 2008, pp. 1207 - 1216

Current copiers:
D. W. J. Groeneveld et al, “A Self-Calibration Technique for Monolithic High-Resolution D/A Converters,” JSSC December 1989, pp. 1517

Dynamic element matching:
R. J. van de Plassche, “Dynamic Element Matching for High-Accuracy Monolithic D/A Converters,” JSSC December 1976, pp. 795

Summary D/A converter

DAC toolchain


Digital
signal
generator
ramp
sine		 DAC:
R-string
Binary R, C
Binary: R2R, C2C		 Oscilloscope
spectrum analyzer
Theory
Simulation
High level
Low level
Circuit
Measurement

1-bit oversampling DAC

Picture of a 1-bit oversampling DAC
Circuit and waveform

Next


08 Sampling and Jitter