Interface Electronics08 ADC Sampling and ErrorProf. Dr. Jörg Vollrath07 DAC practical examples |
Video Lecture: ADC Architectures
|
Länge: 01:06:27 |
0:0:0 Sine histogram by hand 0:0:50 Values in histogram 0:1:22 Pivot table 0:2:34 Sine occurences 0:3:0 Reference 11 periods 0:6:0 Pivot of reference 0:8:45 DNL equation 0:9:14 INL equation 0:10:12 Reference amplitude error 0:12:0 Verification comparing 2 tools and solutions 0:12:56 Laboratory 4 Arduino with ADC, DAC measurement 0:20:14 DAC summary settling time 0:22:34 Timing error 0:23:19 RC low pass 0:24:5 ADC architectures Flash, Pipeline, SAR, Sigma Delta, Dual slope 0:25:37 Resolution and speed 0:28:59 Trade off speed and resolution 0:30:12 ADC Architectures 0:30:59 ADC Signal Chain 0:34:4 ADC Architectures 0:35:31 Ideal Sampling 0:37:37 Real Sampling Switch 0:39:57 RC Time Constant 0:41:17 Clock coupling 0:42:22 Low pass R, C requirement 0:43:41 Upper limit R for speed 0:45:1 Low pass requirement table 0:48:22 R < 0.72/B/fs/C equation 0:50:32 Clock bootstrapping 0:54:25 Clock feed through 0:57:45 Clock feed through compensation 0:59:22 Fully differential sampling 1:0:35 Track and hold sample and hold 1:1:10 Clock jitter 1:4:37 Jitter requirements 1:7:22 Jitter simulation 1:10:7 Spectrum and Jitter analysis 1:10:49 ENOB and Jitter 1:12:43 Summary |
Review and Overview
- ADC architectures, resolution and conversion rate
- AD conversion
- Sampling
- RC circuit
- kT/C Noise
- Acquisition bandwidth
- Switch on resistance
- Bootstrapping
- Fully differential realization
- Clock jitter
Statistical analysis
ADC architectures, resolution and conversion rate
A graph with x axis frequency and y axis resolution shows applications.
Pipeline ADC: 8..16 Bits, 1MHz..4GHz
SAR ADC: 8..18 Bits, 20kHz..8MHz
Sigma Delta ADC: 12..24 Bits, 4Hz..40MHz
Source: QUINTÁNS et al.: METHODOLOGY TO TEACH ADVANCED A/D CONVERTERS, IEEE TRANS. ON EDUCATION, VOL. 53, NO. 3, AUGUST 2010
Investigation of distributer Digikey (01/2017):
Flash ADC (Results: 366): 10 Bit 50 MSps, Range 3..16Bit, 50kHz..26GHz
8 Bit 50kHz AD782 ADI, 3Bit 26GHz HMCAD5831LP9BE ADI, 8 Bit 1GHz MAX104CHC Maxim 16 Bit 166kHz AD7884AQ ADI
Pipeline ADC (Results: 3237): 12 Bit 125MSps, Range 6..16 Bit, 94k..2.6GHz
12 Bit 94kHz MAX1253BEUE+, 12 Bit 2.6GHz ADI, 6 Bit 90MHz MAX1011, 16 Bit 1GHz ADS54 TI
SAR ADC (Results: 8973): 12 Bit 1MSpS, Range 8.. 32Bit 1kSps..500 MSps
32 Bit 1MSps LTC2508 $16, 24 Bit 2MSps LTC2380 $54, 20 Bit 1.6 MSps MX11905 $30 8 Bit 500MSps ISLA118P5 Intersil $50, 8 Bit 3MSps MAX 11116 $2
Sigma Delta ADC(Results: 1928): 24 Bit 256kSps Range: 8..32 Bit , 3Sps..3.2GSps
16 Bit 3.2GSps(100MHz) AD6676 ADI $200, 16 Bit 160MSps(2.5MHz) AD9262 ADI $48, 12 Bit 3.3kSps ADS1015 TI $2, 32Bit 1MSps LTC2508 $17
Dual Slope (Results: 28): 15 Bit 30Sps
Pipeline ADC: 8..16 Bits, 1MHz..4GHz
SAR ADC: 8..18 Bits, 20kHz..8MHz
Sigma Delta ADC: 12..24 Bits, 4Hz..40MHz
Source: QUINTÁNS et al.: METHODOLOGY TO TEACH ADVANCED A/D CONVERTERS, IEEE TRANS. ON EDUCATION, VOL. 53, NO. 3, AUGUST 2010
Investigation of distributer Digikey (01/2017):
Flash ADC (Results: 366): 10 Bit 50 MSps, Range 3..16Bit, 50kHz..26GHz
8 Bit 50kHz AD782 ADI, 3Bit 26GHz HMCAD5831LP9BE ADI, 8 Bit 1GHz MAX104CHC Maxim 16 Bit 166kHz AD7884AQ ADI
Pipeline ADC (Results: 3237): 12 Bit 125MSps, Range 6..16 Bit, 94k..2.6GHz
12 Bit 94kHz MAX1253BEUE+, 12 Bit 2.6GHz ADI, 6 Bit 90MHz MAX1011, 16 Bit 1GHz ADS54 TI
SAR ADC (Results: 8973): 12 Bit 1MSpS, Range 8.. 32Bit 1kSps..500 MSps
32 Bit 1MSps LTC2508 $16, 24 Bit 2MSps LTC2380 $54, 20 Bit 1.6 MSps MX11905 $30 8 Bit 500MSps ISLA118P5 Intersil $50, 8 Bit 3MSps MAX 11116 $2
Sigma Delta ADC(Results: 1928): 24 Bit 256kSps Range: 8..32 Bit , 3Sps..3.2GSps
16 Bit 3.2GSps(100MHz) AD6676 ADI $200, 16 Bit 160MSps(2.5MHz) AD9262 ADI $48, 12 Bit 3.3kSps ADS1015 TI $2, 32Bit 1MSps LTC2508 $17
Dual Slope (Results: 28): 15 Bit 30Sps
ADC architectures, resolution and conversion rate
|
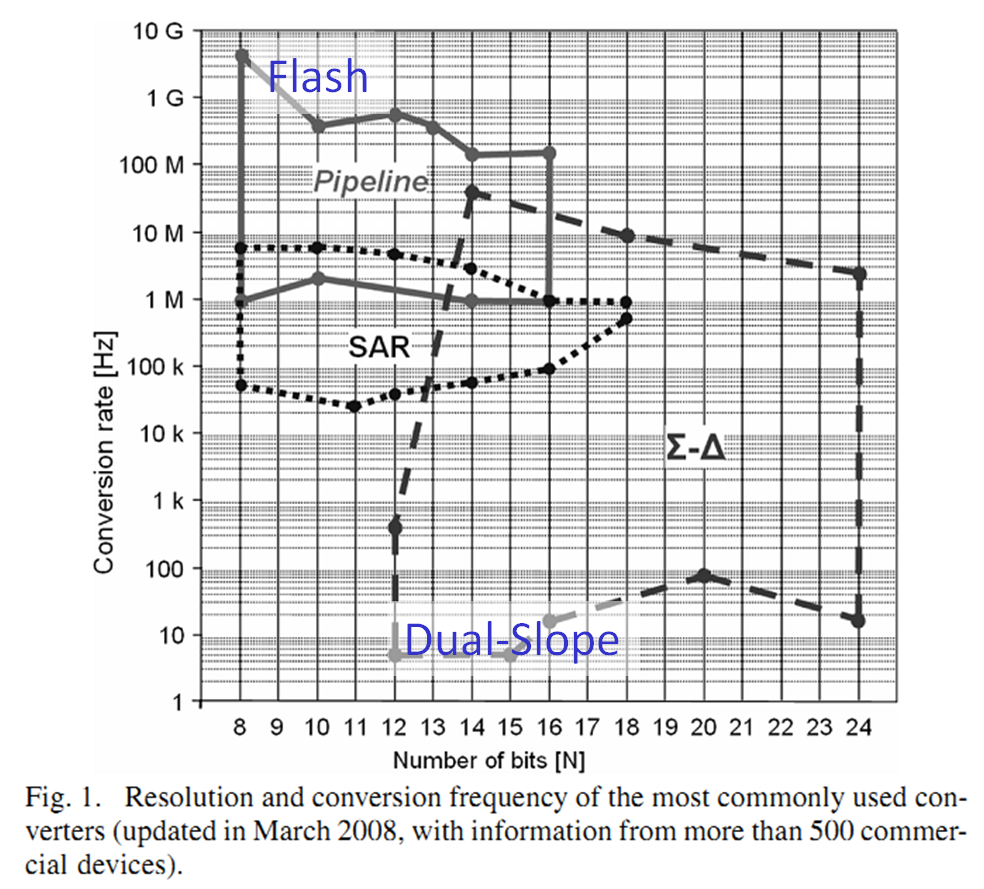 Source: QUINTÁNS et al.: METHODOLOGY TO TEACH ADVANCED A/D CONVERTERS, IEEE TRANS. ON EDUCATION, VOL. 53, NO. 3, AUGUST 2010 |
AD conversion signal chain
Analog signal|
Preamplifier (range adjustment, impedance matching) Anti-alising filter Sampling Quantization Digital coding (error correction, filter) |
 |
Ideal sampling
|
At at time t0 the external voltage is stored internally and fixed until t0+T. The fixed voltage is necessary for a successful conversion. The fixed voltage is necessary to really have the voltage at time t0. The fixed voltage can be easily converted with an ADC. A capacitor is used to store charge to sample the voltage. |
An ideal sample and hold can be used in LTSPICE to analyze switched waveforms.Version 4 SHEET 1 2740 696 WIRE 480 -784 480 -848 WIRE 464 -736 352 -736 WIRE 592 -736 544 -736 WIRE 640 -736 592 -736 WIRE 816 -736 752 -736 WIRE 752 -720 752 -736 WIRE 592 -640 592 -672 WIRE 752 -624 752 -640 FLAG 528 -784 Vtrip FLAG 816 -736 OUT IOPIN 816 -736 Out FLAG 352 -736 IN IOPIN 352 -736 In FLAG 480 -848 clk IOPIN 480 -848 In FLAG 592 -640 0 FLAG 752 -624 0 FLAG 592 -736 VC1 SYMBOL sw 560 -736 R90 WINDOW 3 24 -12 Left 2 WINDOW 38 39 67 Left 2 WINDOW 0 38 33 Left 2 SYMATTR Value "" SYMATTR SpiceModel switmod SYMATTR InstName S1 SYMBOL cap 576 -736 R0 SYMATTR InstName C1 SYMATTR Value 0.5f SYMBOL bv 752 -736 R0 SYMATTR InstName B1 SYMATTR Value V=V(VC1) TEXT 392 -576 Left 2 !.model switmod SW TEXT 328 -936 Left 2 !VT VTRIP 0 DC 0.5 |
Real sampling
|
Transistor is used as a switch. A transistor is on for half the sampling period. During this time the signal is tracked. Then the transistor is turned off and the charge and voltage fixed on the capacitor. The transistor has a finite resistance, limiting the bandwidth of the RC circuit. The resistance has thermal noise which can limit the resolution (number of bits) of the ADC. The control clock of the gate of the transistor is capacitively coupling to the stored voltage. The transistor source has a leakage current discharging the capacitance. The input voltage source has to be able to drive enough current to charge the capacitance. |
Version 4 SHEET 1 880 680 WIRE 288 16 208 16 WIRE 288 32 288 16 WIRE 272 80 208 80 WIRE 400 80 368 80 WIRE 208 144 208 80 WIRE 208 144 176 144 WIRE 320 144 320 80 WIRE 320 144 304 144 WIRE 400 144 400 80 WIRE 432 144 400 144 WIRE 320 160 288 160 WIRE 288 176 288 160 WIRE 400 208 400 144 WIRE 464 208 400 208 WIRE 208 224 208 144 WIRE 272 224 208 224 WIRE 320 224 320 160 WIRE 400 224 400 208 WIRE 400 224 368 224 WIRE 352 288 352 272 WIRE 352 288 208 288 WIRE 464 336 464 272 FLAG 208 288 CLK IOPIN 208 288 In FLAG 176 144 A IOPIN 176 144 BiDir FLAG 432 144 B IOPIN 432 144 BiDir FLAG 464 336 0 FLAG 208 16 CLKb IOPIN 208 16 In FLAG 304 144 VDD FLAG 288 176 0 SYMBOL pmos4 368 32 R90 SYMATTR InstName M3 SYMATTR Value P SYMATTR Value2 l=50n w=250n ad=0.029P as=0.016P pd=0.742U ps=0.363U m=1600 SYMBOL nmos4 272 272 R270 SYMATTR InstName M4 SYMATTR Value N SYMATTR Value2 l=50n w=250n ad=0.016P as=0.022P pd=0.363U ps=0.629U m=1600 SYMBOL cap 448 208 R0 SYMATTR InstName C2 SYMATTR Value 10n |
Sampling network low pass thermal noise
A resistor has a noise voltage:\frac{V_{rms}^2}{\Delta f} = 4 k_B \cdot T \cdot R
A low pass RC network limits the noise to:
\overline{v_n^2} = \frac{k_B T}{C}
This noise has to be lower than the quantization noise:
\overline{v_q^2} = \frac{\Delta^2}{12} = \frac{V_{FS}^2}{2^{2B} \cdot 12}
Sampling network thermal noise capacitance requirement
C \gt 12 \cdot k_B \cdot T \frac{2^{2 B}}{V_{FS}^{2}}kB: Boltzmann constant (1.38 · 10 -23 m2kg s-2K-1)
T: absolute temperature in Kelvin
B: number of Bits
VFS: Full scale voltage
| B | Cmin(V |
Cmin(V |
| 8 | 0.3 fF | 0.003 pF |
| 12 | 80 fF | 0.8 pF |
| 16 | 20.6 pF | 206 pF |
| 20 | 5.28 nF | 52.8 nF |
| 24 | 1.32 uF | 13.2 uF |
Adding 4 bits required an increase in capacitance by a factor of 256.
Decreasing the voltage by a factor of 3.3 increases the capacitance with a factor of 10.
Sampling network low pass requirement
|
The sampling network has a transfer function of: \underline{T}(j\omega) = \frac{\underline{U}_a}{\underline{U}_e} = \frac{\frac{1}{j\omega C}}{R + \frac{1}{j\omega C} } \underline{T}(j\omega) = \frac{1}{j \omega C R + 1 } The difference in magnitude should be less than 1/2 LSB. Lets look at a normalized transfer function \Omega = \omega C R \underline{T}(j\Omega) = \frac{1}{j \Omega + 1 } |
To prevent gain error from the signal transfer function \frac{1}{| j \Omega + 1 |} \gt (1 - 0.5 \frac{LSB}{V_{ref}} ) \frac{1}{| j \Omega + 1 |} \gt (1 - \frac{1}{2^{B+1}} ) \Omega^{2} \lt \frac{1}{(1 - \frac{1}{2^{B+1}} )^2} - 1 \Omega \lt \frac{1}{2^\frac{B}{2}} 2 \pi \frac{f_g}{2} R C \lt \frac{1}{2^\frac{B}{2}} R \lt \frac{1}{\pi \cdot f_g \cdot C \cdot 2^\frac{B}{2}} |
To prevent gain error from the signal transfer function
\frac{1}{| j \Omega + 1 |} \gt (1 - 0.5 \frac{LSB}{V_{ref}} )
\frac{1}{| j \Omega + 1 |} \gt (1 - \frac{1}{2^{B+1}} )
\frac{1}{\sqrt{ \Omega^{2} + 1 }} \gt (1 - \frac{1}{2^{B+1}} )
\frac{1}{(1 - \frac{1}{2^{B+1}} )^2} \gt \Omega^{2} + 1
\Omega^{2} \lt \frac{1}{(1 - \frac{1}{2^{B+1}} )^2} - 1
\Omega^{2} \lt \frac{1 - 1 + \frac{1}{2^B}- \frac{1}{2^{2B+2}}}{(1 - \frac{1}{2^{B+1}} )^2}
\Omega^{2} \lt \frac{\frac{1}{2^B} \left( 1 - \frac{1}{2^{B+2}} \right) }{(1 - \frac{1}{2^{B+1}} )^2} \approx \frac{1}{2^B}
\Omega \lt \frac{1}{2^\frac{B}{2}}
2 \pi \frac{f_g}{2} R C \lt \frac{1}{2^\frac{B}{2}}
R \lt \frac{1}{\pi \cdot f_g \cdot C \cdot 2^\frac{B}{2}}
\frac{1}{| j \Omega + 1 |} \gt (1 - 0.5 \frac{LSB}{V_{ref}} )
\frac{1}{| j \Omega + 1 |} \gt (1 - \frac{1}{2^{B+1}} )
\frac{1}{\sqrt{ \Omega^{2} + 1 }} \gt (1 - \frac{1}{2^{B+1}} )
\frac{1}{(1 - \frac{1}{2^{B+1}} )^2} \gt \Omega^{2} + 1
\Omega^{2} \lt \frac{1}{(1 - \frac{1}{2^{B+1}} )^2} - 1
\Omega^{2} \lt \frac{1 - 1 + \frac{1}{2^B}- \frac{1}{2^{2B+2}}}{(1 - \frac{1}{2^{B+1}} )^2}
\Omega^{2} \lt \frac{\frac{1}{2^B} \left( 1 - \frac{1}{2^{B+2}} \right) }{(1 - \frac{1}{2^{B+1}} )^2} \approx \frac{1}{2^B}
\Omega \lt \frac{1}{2^\frac{B}{2}}
2 \pi \frac{f_g}{2} R C \lt \frac{1}{2^\frac{B}{2}}
R \lt \frac{1}{\pi \cdot f_g \cdot C \cdot 2^\frac{B}{2}}
Sampling network low pass requirement table
| Bits, frequency [fg] | Ua [V] | 1 - 20*log(Ua) |
| ∞ ,DC | 1 | 0 dB |
| 24, 0.00024 | 0.99999994 | -0.0000006 dB |
| 20, 0.0097 | 0.99999905 | -0.000008 dB |
| 16, 0.0039 | 0.999985 | -0.00013 |
| 12, 0.0156 | 0.9976 | -0.0021 |
| 8, 0.0625 | 0.996 | -0.034 |
Sampling network voltage difference requirement
The capacitor has to be charged to the 1/2 LSB range of the input voltage:| V_e - V_a | < 0.5 LSB
The voltage on the capacitor is:
V_a = V_e \cdot \left( 1 - exp^{-\frac{t}{\tau}} \right) with \tau = RC
This gives:
V_e - V_e \cdot \left( 1 - exp^{-\frac{t}{\tau}} \right) < 0.5 LSB V_e \cdot e^{-\frac{t}{\tau}} < 0.5 LSB
Maximum difference could be full scale V_e = 2^{B} \cdot LSB with B number of bits:
| 2^{B} \cdot LSB \cdot exp^{-\frac{t}{\tau}} < 0.5 LSB | exp^{-\frac{t}{\tau}} < 2^{-N-1} |
| -\frac{t}{\tau} < ln \left( 2^{-B-1} \right) | -\frac{t}{\tau} < \left( -B-1 \right) ln \left( 2 \right) |
| t > R C \left( B+1 \right) ln \left( 2 \right) |
R < \frac{1}{2 \cdot f \cdot C \left( B+1 \right) ln \left( 2 \right) } = \frac{0.72}{ f_{sample} \cdot C \left( B+1 \right) }
Sampling network voltage difference resistance requirement
R \lt \frac{0.72}{B \cdot f_s \cdot C}fs: Sampling frequency (half period active and switch closed)
B : number of bits
C: sampling capacitance
| B, C | fS = 10MHz | fS = 100MHz | fS = 1GHz |
| 8,3.26fF | 2.76MΩ | 276.3kΩ | 27.63kΩ |
| 12,833.88fF | 7.2kΩ | 719.52Ω | 71.95Ω |
| 16,213.47pF | 21.08Ω | 2.11Ω | 210.8mΩ |
| 20,54.65nF | 65.87mΩ | 6.59mΩ | 658.74μΩ |
| 24,13.99μF | 214.44μΩ | 21.44μΩ | 2.14μΩ |
Since these values are very low and can not be realized, higher values are used and a digital filter or error correction is required to adjust the frequency response.
This process with the measured RDSon in the range of kΩ can realisticly achieve:
1GHz, 10 Bit;
100 MHz, 12 Bit;
10 MHz, 14 Bit;
Clock bootstrapping
Achieve a constant resistance of the switch by using a constant overdrive.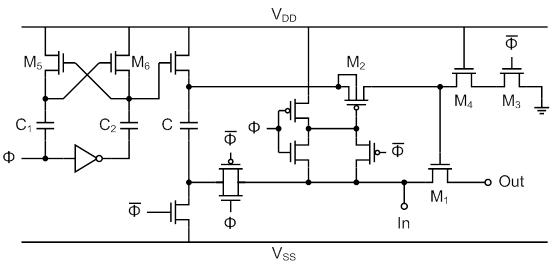
Ref: A. M. Abo and P. R. Gray, “A 1.5-V, 10-bit, 14.3-MS/s CMOS pipeline ADC,” IEEE Journal of Solid-State Circuits, vol. 34, issue 5, pp. 599-606, 1999.
Clock feed through
|
The clock signal is coupling via the switch transistor capacitance to the signal. Voltage coupling depends on load capacitance. A charge is specified. Example: TI switch: ts3a44159 |
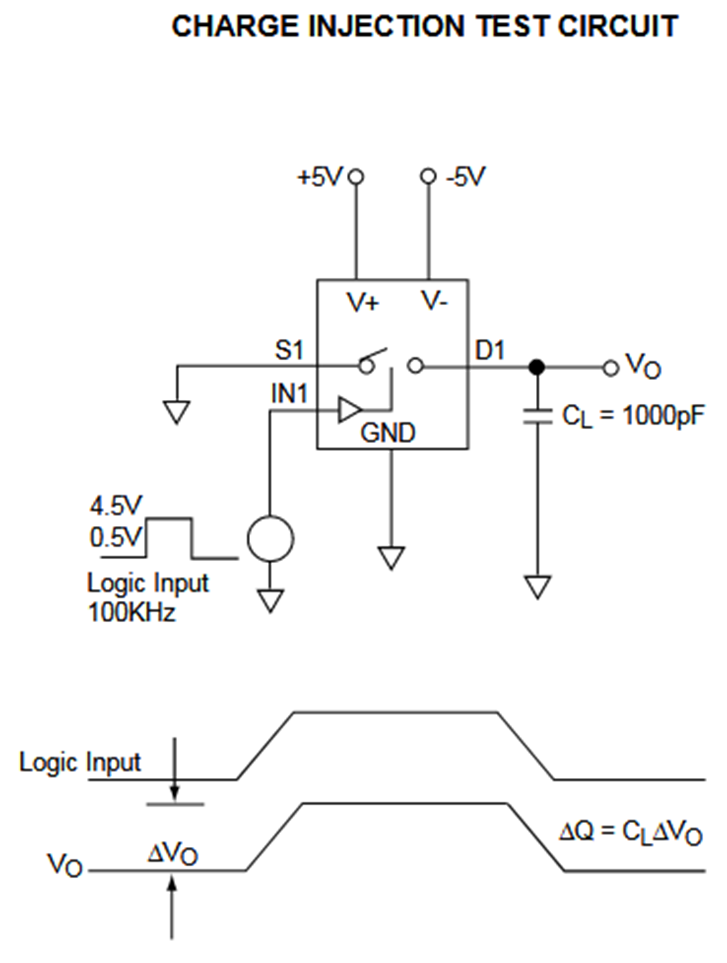 Source: data sheet ALD4201/ALD4202M Advanced Linear devices |
Clock feed through compensation
|
Compensation with dummy transistors:
|
Version 4 SHEET 1 880 680 WIRE 272 -128 224 -128 WIRE 384 -128 368 -128 WIRE 112 -64 96 -64 WIRE 288 -64 256 -64 WIRE 352 -64 352 -80 WIRE 352 -64 288 -64 WIRE 448 -64 416 -64 WIRE 112 -48 112 -64 WIRE 288 -48 288 -64 WIRE 416 -48 416 -64 WIRE 96 0 64 0 WIRE 224 0 224 -128 WIRE 224 0 192 0 WIRE 272 0 224 0 WIRE 320 0 320 -128 WIRE 384 0 384 -128 WIRE 384 0 368 0 WIRE 400 0 384 0 WIRE 544 0 496 0 WIRE 64 128 64 0 WIRE 224 128 224 0 WIRE 224 128 64 128 WIRE 384 128 384 0 WIRE 544 128 544 0 WIRE 544 128 384 128 WIRE 64 144 64 128 WIRE 64 144 32 144 WIRE 144 144 144 0 WIRE 304 144 144 144 WIRE 320 144 320 0 WIRE 320 144 304 144 WIRE 448 144 448 0 WIRE 448 144 320 144 WIRE 544 144 544 128 WIRE 576 144 544 144 WIRE 288 160 160 160 WIRE 320 160 288 160 WIRE 432 160 320 160 WIRE 64 176 64 144 WIRE 208 176 64 176 WIRE 288 176 288 160 WIRE 544 176 544 144 WIRE 544 176 384 176 WIRE 64 320 64 176 WIRE 112 320 64 320 WIRE 160 320 160 160 WIRE 208 320 208 176 WIRE 272 320 208 320 WIRE 320 320 320 160 WIRE 384 320 384 176 WIRE 384 320 368 320 WIRE 432 320 432 160 WIRE 544 320 544 176 WIRE 544 320 480 320 WIRE 192 384 192 368 WIRE 192 384 144 384 WIRE 352 384 352 368 WIRE 352 384 288 384 WIRE 464 384 464 368 WIRE 464 384 448 384 WIRE 288 416 288 384 WIRE 208 464 208 320 WIRE 272 464 208 464 WIRE 320 464 320 320 WIRE 384 464 384 320 WIRE 384 464 368 464 FLAG 288 384 CLK IOPIN 288 384 In FLAG 32 144 A IOPIN 32 144 BiDir FLAG 576 144 B IOPIN 576 144 BiDir FLAG 256 -64 CLKb IOPIN 256 -64 In FLAG 304 144 VDD FLAG 288 176 0 FLAG 96 -64 CLK IOPIN 96 -64 In FLAG 448 -64 CLK IOPIN 448 -64 In FLAG 144 384 CLKb IOPIN 144 384 In FLAG 448 384 CLKb IOPIN 448 384 In SYMBOL pmos4 368 -48 R90 SYMATTR InstName M3 SYMATTR Value CD4007P SYMATTR Value2 m=100 SYMBOL nmos4 272 368 R270 SYMATTR InstName M4 SYMATTR Value CD4007N SYMATTR Value2 m=100 SYMBOL pmos4 496 -48 R90 SYMATTR InstName M1 SYMATTR Value CD4007P SYMATTR Value2 m=100 SYMBOL pmos4 192 -48 R90 SYMATTR InstName M2 SYMATTR Value CD4007P SYMATTR Value2 m=100 SYMBOL nmos4 384 368 R270 SYMATTR InstName M5 SYMATTR Value CD4007N SYMATTR Value2 m=100 SYMBOL nmos4 112 368 R270 SYMATTR InstName M6 SYMATTR Value CD4007N SYMATTR Value2 m=100 SYMBOL pmos4 272 -80 R270 SYMATTR InstName M7 SYMATTR Value CD4007P SYMATTR Value2 m=100 SYMBOL nmos4 368 416 R90 SYMATTR InstName M8 SYMATTR Value CD4007N SYMATTR Value2 m=100 |
The following imperfections occur:
Capacitive coupling from clock to the input and output.
Charge during the on state in the channel has to be compensated.
CLK and CLKb have to symmetric. Use a real clock signal from an inverter to estimate asymmetry.
Capacitive coupling from clock to the input and output.
Charge during the on state in the channel has to be compensated.
CLK and CLKb have to symmetric. Use a real clock signal from an inverter to estimate asymmetry.
Fully differential sample and hold
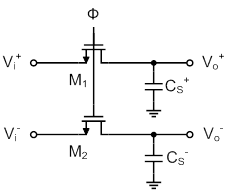
FullyDifferentialTH
Clock jitter and signal sampling
|
Random variations in the period of the clock is called clock jitter.
This can happen due to power noise or signal noise.
Long lines and buffer stages can increase clock jitter. What errors are induced by clock jitter? INL, DNL, signal to noise ratio. The yellow curve shows the ideal waveform. Clock jitter causes to sample data earlier or later (green curve). This causes error due to the change in signal level (blue curve). This causes error (red curve) reflected in INL, DNL and signal to noise ratio. |
|
Clock jitter requirements
|
What are requirements for clock jitter? Clock jitter has to be smaller than 1 LSB. Signal: V(t) = 2^{N-1} \cdot LSB \cdot sin \left( \omega t \right) Amplitude is: 2^{N-1} \cdot LSB The slope is: V'(t) = 2^{N-1} \cdot LSB \cdot \omega \cdot cos \left( \omega t \right) Maximum change in signal after dt should be smaller than LSB: 2^{N-1} \cdot LSB \cdot \omega \cdot dt \lt LSB dt \lt \frac{1}{2 \cdot \pi \cdot f_{signal} \cdot 2^{N-1} } = \frac{1}{ \pi \cdot f_{sampling} \cdot 2^{N} } Higher signal frequency or greater amplitude will increase the signal change after dt and increases jitter errror. |
|
Statistical jitter analysis
Calculation of the mean squared jitter error (variance)sinusoidal signal
x(t) = A sin(2 π fx t)
then
x’(t) = 2 π fx A cos(2 π fx t)
E{[x’(t)]2} = 4 π 2 fx2 A 2
Jitter variance E{(tJ-t0) 2 } = σ 2
If x’(t) and the jitter are independent
– E{[x’(t)(tJ-t0)] 2} = E{[x’(t)] 2} E{(tJ-t0) 2}
Hence, the jitter error power is
E{e2} = 4 π2 fx2 A2 σ2
If the jitter is uncorrelated from sample to sample, this “jitter noise” is white
DR_{jitter} = \frac{\frac{A^2}{2}}{2 \pi^2 f_x^2 A^2 \sigma^2}
DR_{jitter} = \frac{1}{2 \pi^2 f_x^2 \sigma^2}
ADR_{jitter} = - 20 log_{10} \left( 2 \pi f_x \sigma \right)
DR: Distortion ratio
Ratio of power of Sine signal and power of jitter noise.
A: Amplitude
fx: frequency
σ2:jitter variance
Spectrum and jitter analysis
|
Clock jitter has a spectrum and degrades the signal to noise ratio. Clock jitter can be simulated: AD Characteristic The jitter error is specified with standard devitation regarding sampling clock period. To have errors smaller than one period the error should eb smaller than 0.1 The signal has an offset of 0.5 and an amplitude of 0.5. This gives -9 dB for the signal. |
Simulated total noise level with jitter: ADC Simulation
Signal: -9.03 dB Quantization noise level: -58 dB Change in std deviation of factor of 2 gives 6 dB, one bit. |
ENOB and jitter
|
Calculate signal to noise at different frequencies. If you have frequency dependent signal to noise ratio calculate jitter variance. Problem for subsampling. ADC Simulation 17,53,173,601 and 1731 periods. Noise error:0.1, 0.05, 0.005 Math.sin((i + jitter * randomNormal(0.5) ) / Npair * 2 * Math.PI * nPeriod) |
Summary
- Pick a capacitor according to the resolution of the ADC
- Select a low resistance for the switch
- Clock coupling should be measured
- Both can be compensated by digital filtering and error correction
- Jitter can limit the signal to distortion ratio and should be eliminated with careful clock design.
- Jitter can be identified measuring noise level with varying signal amplitude and frequency.
- Use appropriate capacitances for all signal nodes and power supply.
- Differential signaling can minimize external signal interference.
References
Resitor thermal noise: https://en.wikipedia.org/wiki/Johnson%E2%80%93Nyquist_noise
Next:
09 ADC Architecture