Interface ElectronicsLab04 R2R DACGroupE00 ***700, C |
Overview
- Building a 8-bit R2R DAC in LTSpice
- Simulation of R2R DAC
- Building 8-bit R2R DAC
- Implementation of real circuit
- Frequency limit of the converter
- Code steps settling times
- Ramp DNL and INL analysis
- Sine FFT analysis
- Calibration Process and Results
- Problems during the practical execution
- Conclusions
The following report describes the results delivered by the conduction of the Lab Instruction
Building a 8-bit R2R DAC in LTSpice
|
The following circuit was build as an extension from the 4-bit R2R DAC. The measurement of the resistance gave the following results:
|
Simulation of R2R DAC
|
A symbol from the previous circuit was created. It was attached to the test circuit from Lab03 and two blocks of 4-bit ADC were configured as well in order to form a 8-bit ADC. The input voltages were considered the same wave: Sine and Ramp |
RampWave Output Result
|
The image shows the result of a ramp wave input. It can be seen the discretization levels of the ramp wave over the time. As the converter has 8 bits, therefore the number of available code are as follows: \( {CODES} = {2^{N}} = 2^{8} = 256 \) The LSB can be calculated from the following formula: \( LSB = \frac{V_ref}{2^{N}} = \frac{1{V}}{256}= 390.6{µ V} \) and therefore, the maximum output voltage is: \( V_{out,max} = {LSB} \times ({2^{N}-1}) \) \( = 390.6{µ V} \times 255 ≈ 996.1{mV} \) |
|
RampWave INL and DNL analysis
The following image is a result of the processed data by the Raw Data Analysis.
It shows the DNL and INL graphics for the rampwave.
It can be seen that the extracted and the ideal curve are nearly the same. However
there is a small DNL error which can be seen clearly in the accumulation ramp of the
INL, and periodically, there is big error in the DNL which changes the offset of the
INL ramp. Additionally, the magnitude of the error is quite small, and for a real
measurement perhaps accurate instruments are required. Here it can be seen the effect
of the uncompensated values of the resistances.
RampWave Histogram analysis
The following image shows the DNL and INL error for the histogram analysis. As the
number of occurrences is the same for all the codes, theoretically there is no DNL
error, which implies no INL error as well.
SineWave Output Result
The image shows the result of a sine wave input. It can not be
seen the discretization levels of the sine wave over the time,as
it seem a continuous signal, but with a zoom into it, the discretization
levels can be seen.
SineWave Histogram analysis
The following image shows the DNL and INL error for the histogram analysis. The
number of occurrences of the codes is not equally distributed, because the sine wave
has more samples at the peaks of the wave (non-linear function). These peaks are mostly
represented by the codes 0 and 255, and the DNL is proportional to the number of
measurements for each code. That is also the reason that for the codes for the linear
region of the sine wave, the error is minimum (codes 127 - 128).
SineWave FFT analysis
The figure shows the FFT analysis for the sine wave. The number of points choosen for
the FFT was 4096. The amplitude of the voltage is 0.5 V, Offset 0.5 V, 11 periods.
SineWave FFT analysis
|
The magnitude for the frequency 11 is as follows: \( {FFT_{power}} = 20 \times \log (\frac{0.5 V}{\sqrt 2}) ≈ -9{dB}\) \( Power ≈ 6{dB} \times 7 ≈ 42{dB}\) So the peak of the signal is: \( Peak = 42 {dB} - 6 {dB} ≈ 36{dB} \) The SNR defined for an 8-bit converter is: \( SNR = (6.02 {dB} \times 8) + 1.76 {dB} ≈ 49.9{dB} \) Therefore the noise floor will have a magnitude of: \( Noise = 36 {dB} - 49.9 {dB} = -13.9{dB} \) As the noise is spreaded over 256 bins, the noise level in FFT is: \( {Noise}_{FFT} = -13.9{dB} - 10 \times \log ({2^{N}}) = -13.9{dB}-24{dB} = -37.9{dB} \) |
SineWave FFT analysis
The previous theoretical data seems to match with the FFT graphic, as well as the
SNR results presented in the following image:
Real 8-bit DAC Circuit
Now, from the previous schematic, the R2R DAC structure was implemented on bread board.
The following image shows the physical distribution of the circuit and the conection between Electronic Explorer.

Measurements
Ramp wave input
These are the following measurements made to the circuit.
- Output Voltages for 1KHz, 10KHz and 100Khz
- Settling Times
- Maximum Voltage
- LSB
- Offset
Measurements
Output waveforms
The following images show the output wave form of the DAC - R2R, where for each image and for all in this document
the orange line represents the bit 8 of the converter (MSB), and the blue one represents the output analog voltage.
The frequencies were choosen acording to the instructions of the lab (1Khz, 10Khz, 100Khz),
the output frequency of the analog and also the MSB is not the same. I guess the selected parameter refers to the frequency
of the bit 1 of the converter (LSB).
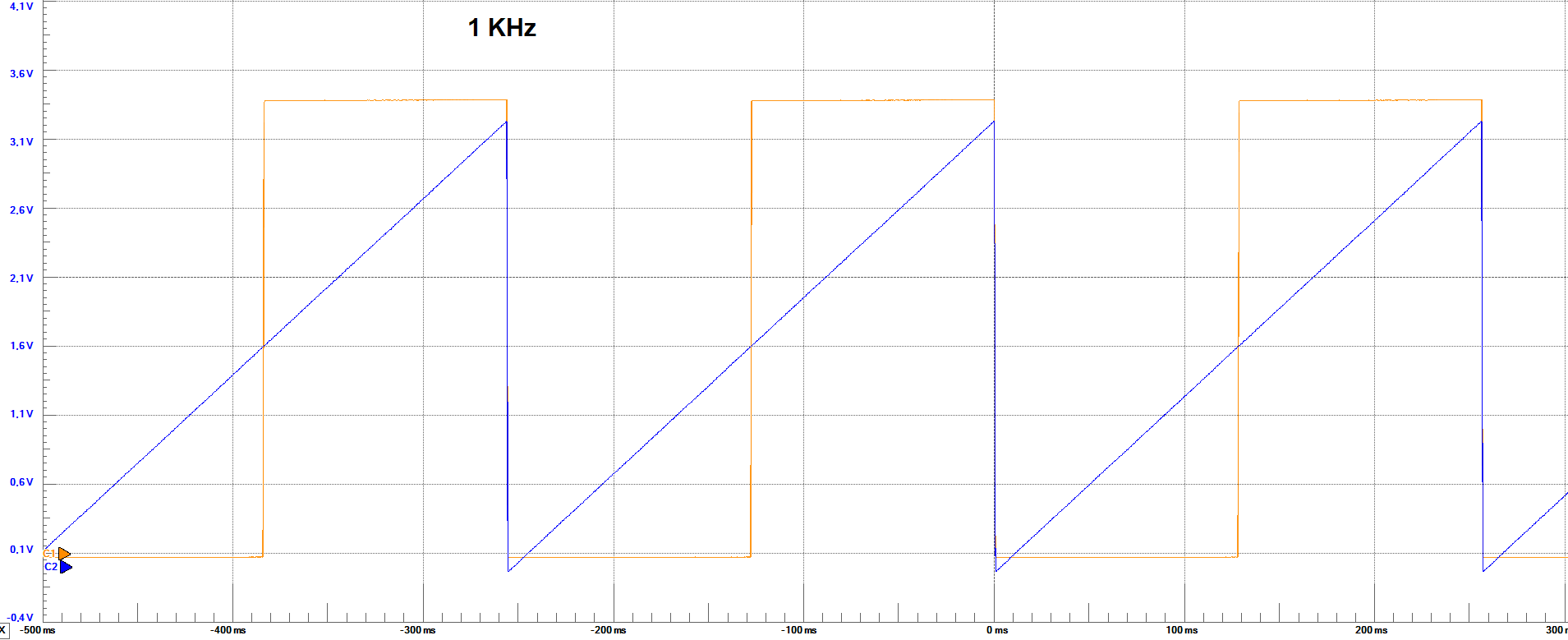
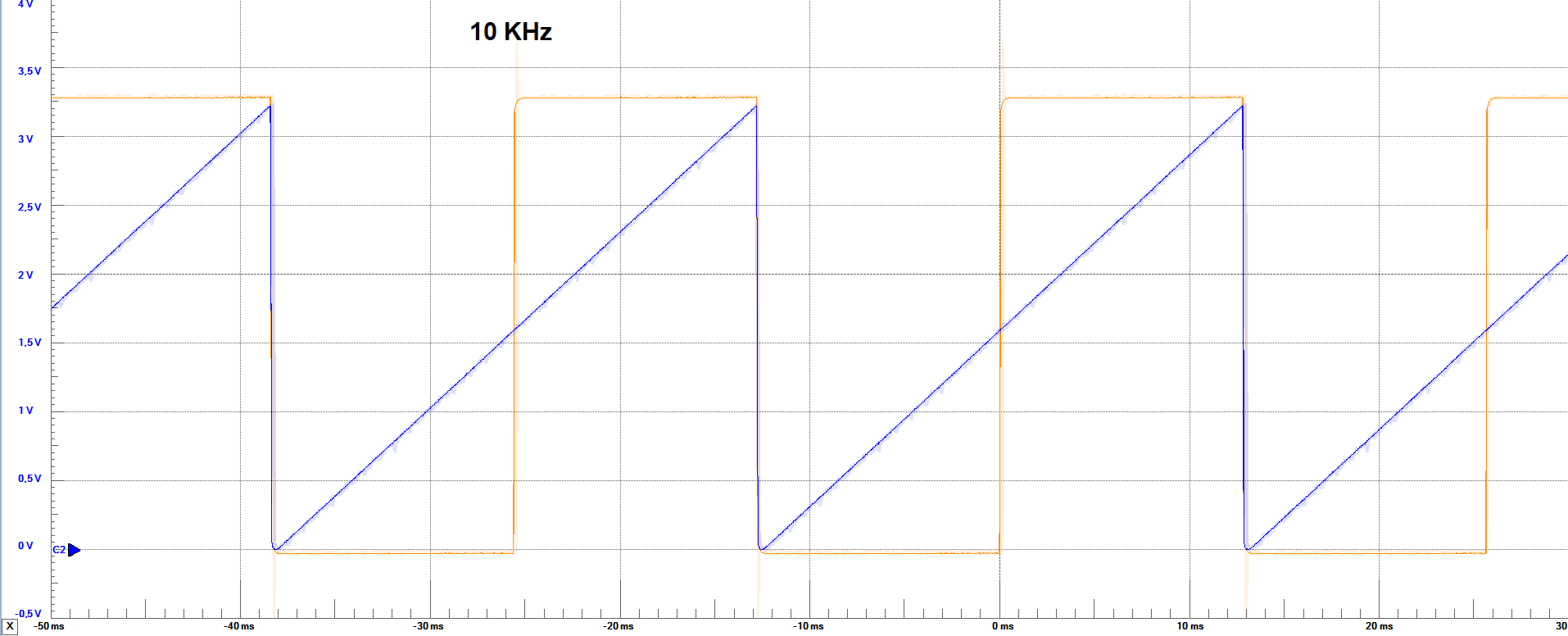
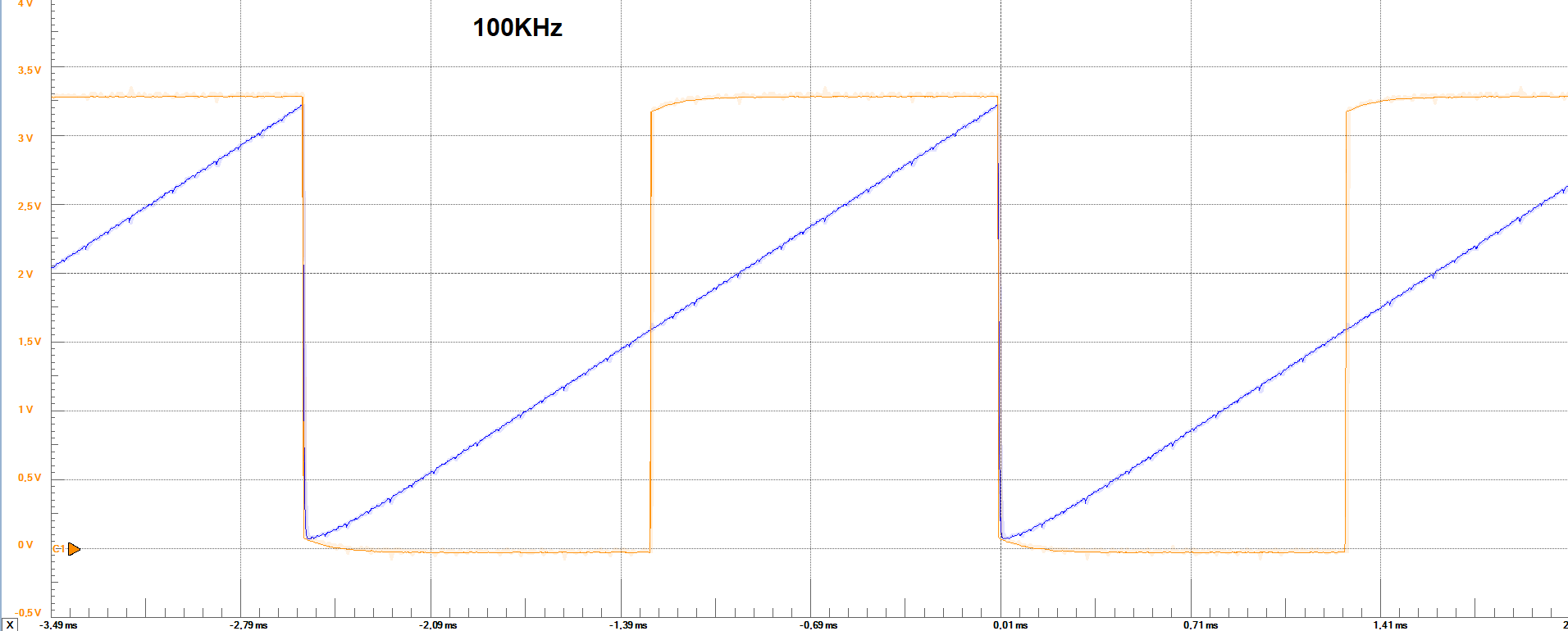
Measurements
Output waveforms Analysis
The following are the frequency of the output voltage signal, and maximum and minimum output voltage acording to the previous images.
| Set Parameter | 1KHz | 10KHz | 100KHz |
| Output Freq. | ≈ 3.9 Hz | ≈ 39 Hz | ≈ 391 Hz |
| Max. Voltage | ≈ 3.2 V | ≈ 3.2 V | ≈ 3.2 V |
| Min. Voltage | ≈ -0.3 V | ≈ 0 V | ≈ 100 mV |
From the images, we could also say that with every increase in the frequency, the output waveform gets more deformated on the edges of the ramp.
Also, with the high frequency, the minimum voltage of the output voltage is not reaching the same values of the slow one, which could be an
indication that some codes are being missing due to the fast change in all bit states. Besides this observations, it can be seen that for some
points in the graphics, there is some kind of overshoot (spikes), for the frequencies 10Khz and 100Khz, not presented in the 1Khz frequency.
Measurements
The following images show the outputwave form of the DAC - R2R with the goal to measure the settling times (falling and rising) by changing just 1 code step and full code step
The orange line represents the bit 8 of the converter (MSB), and the blue one represents the output analog voltage.
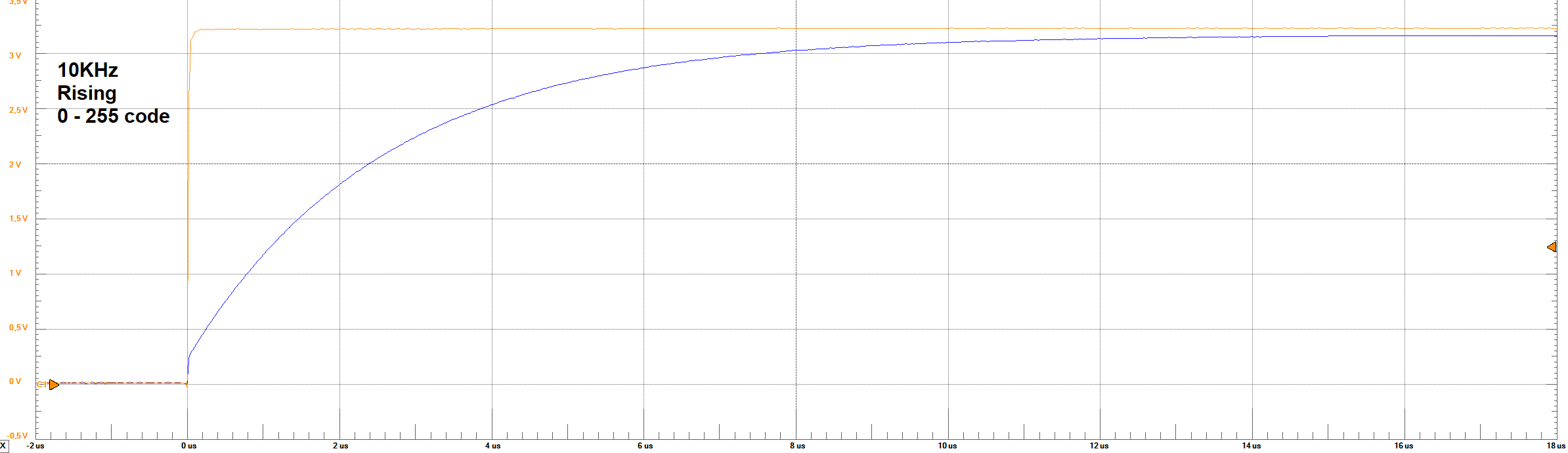
Settling Times - 10 KHz - 0 to 255 code step
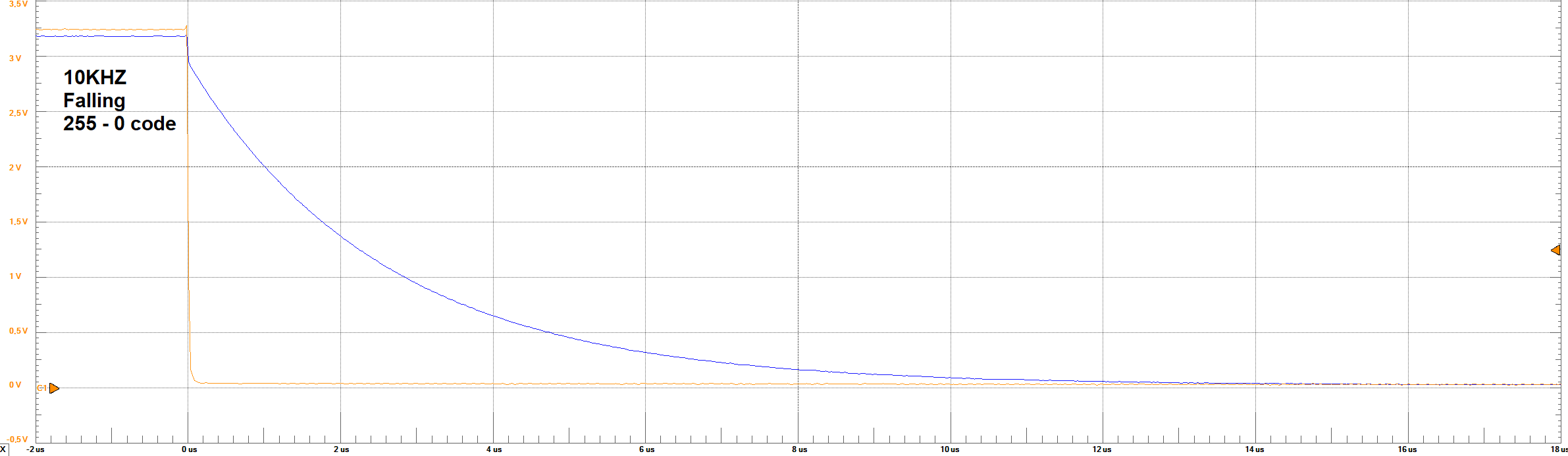
Measurements
Settling Times - 10 KHz - 127 to 128 code step
The orange line represents the bit 8 of the converter (MSB), and the blue one represents the output analog voltage.
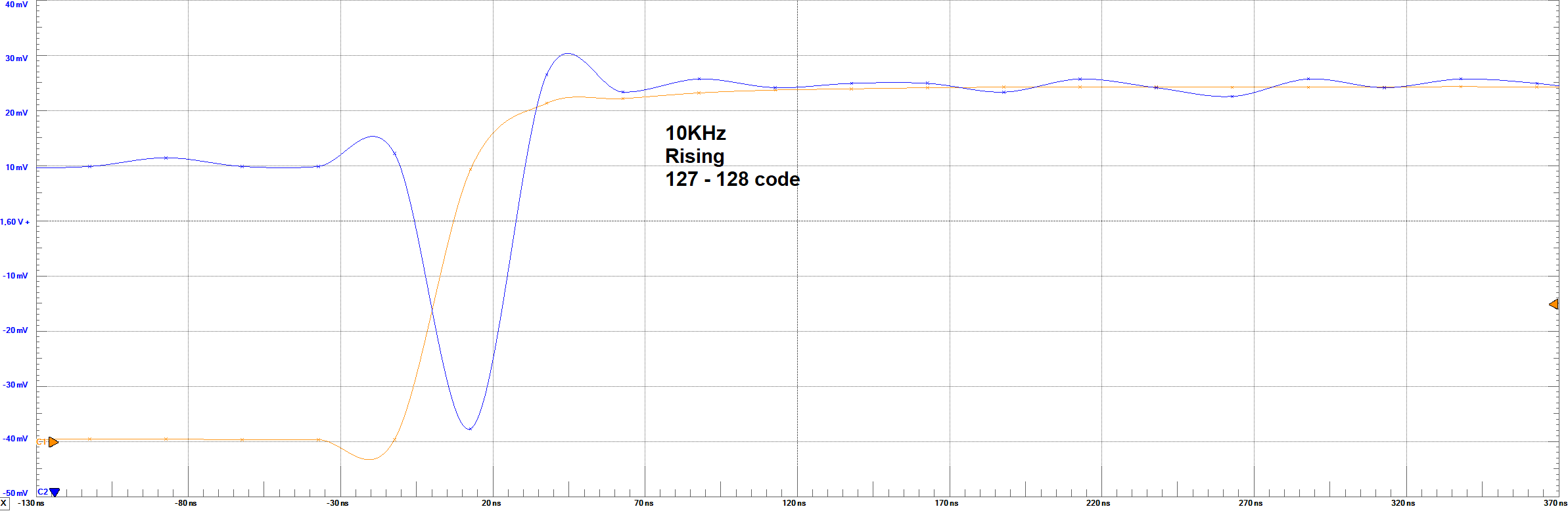
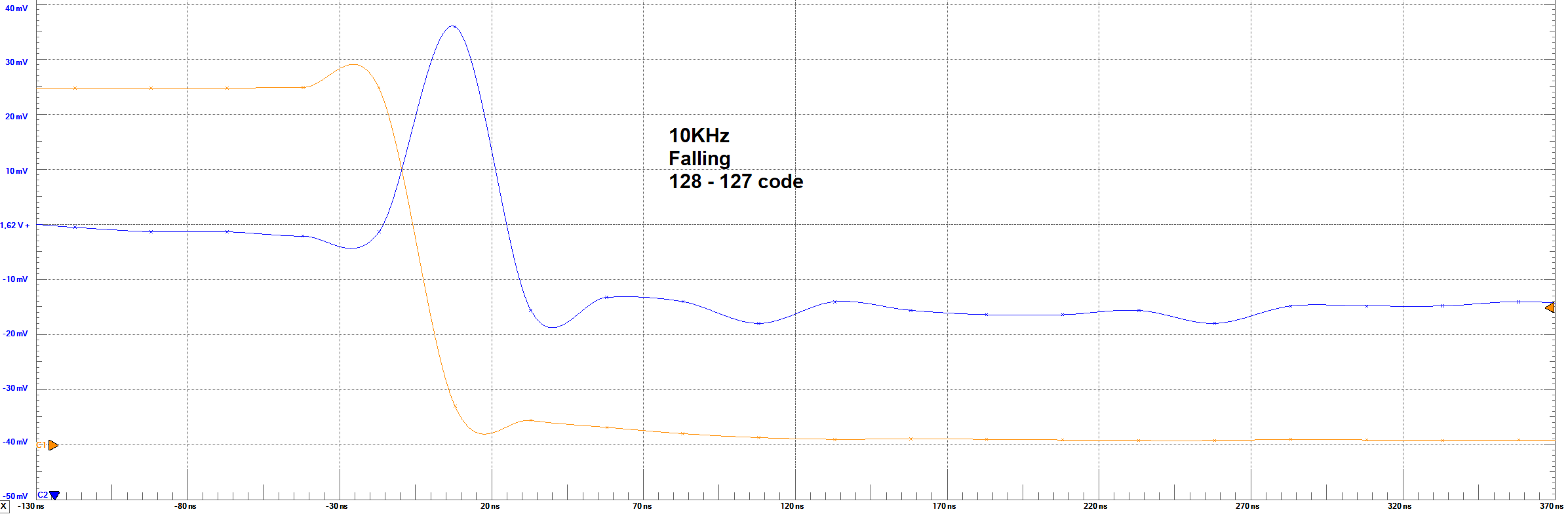
Measurements
Settling Times - 100 KHz - 0 to 255 code step
The orange line represents the bit 8 of the converter (MSB), and the blue one represents the output analog voltage.
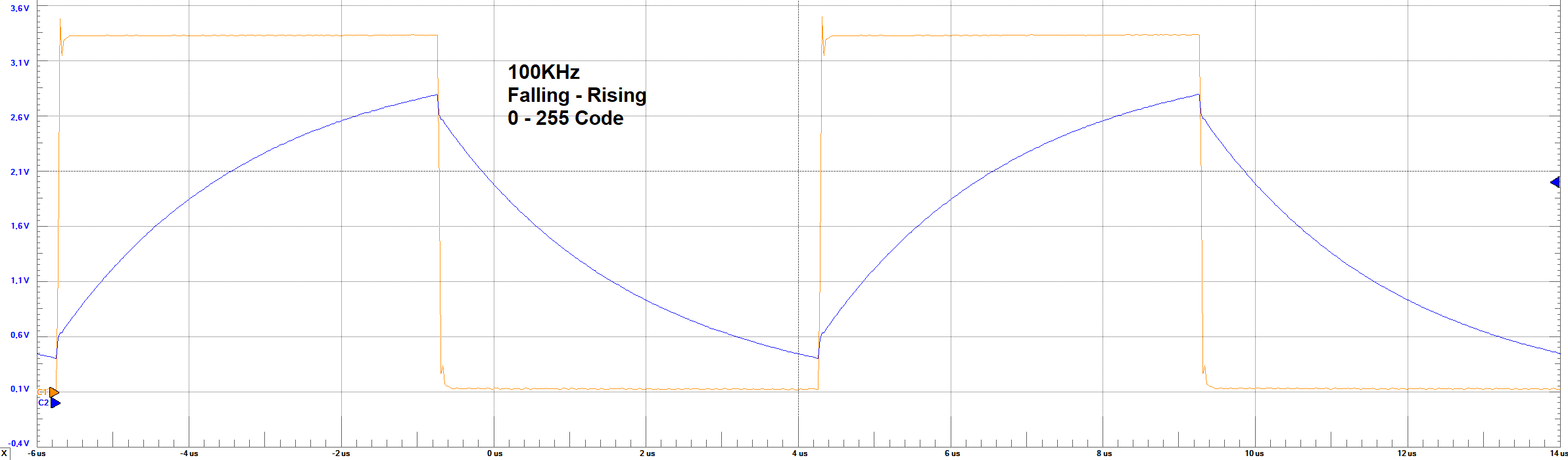
Measurements
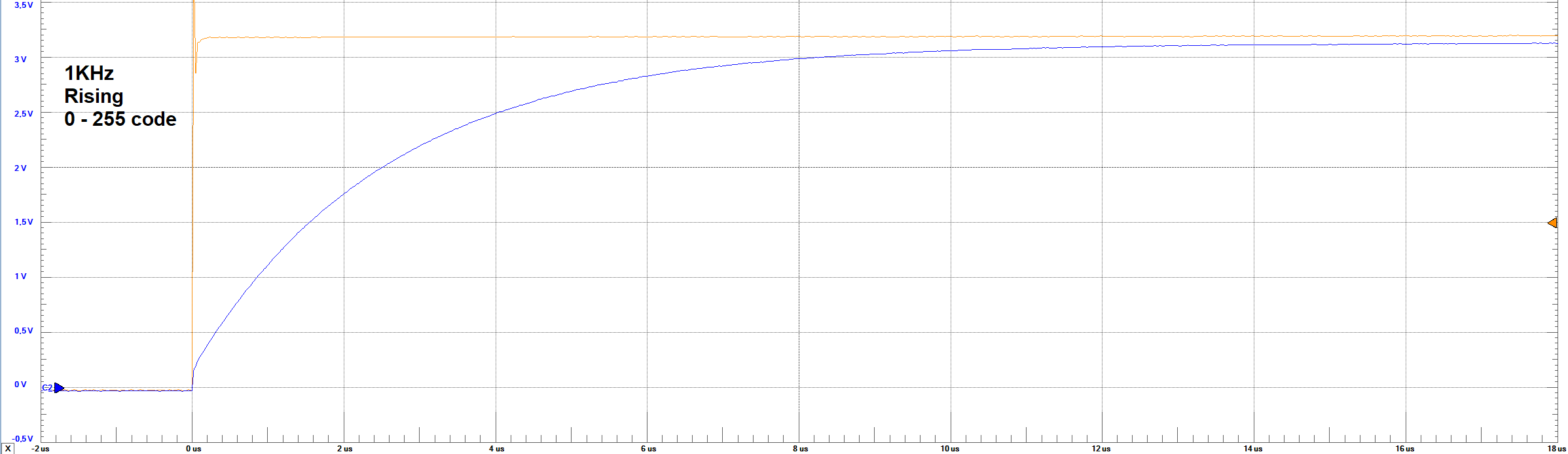
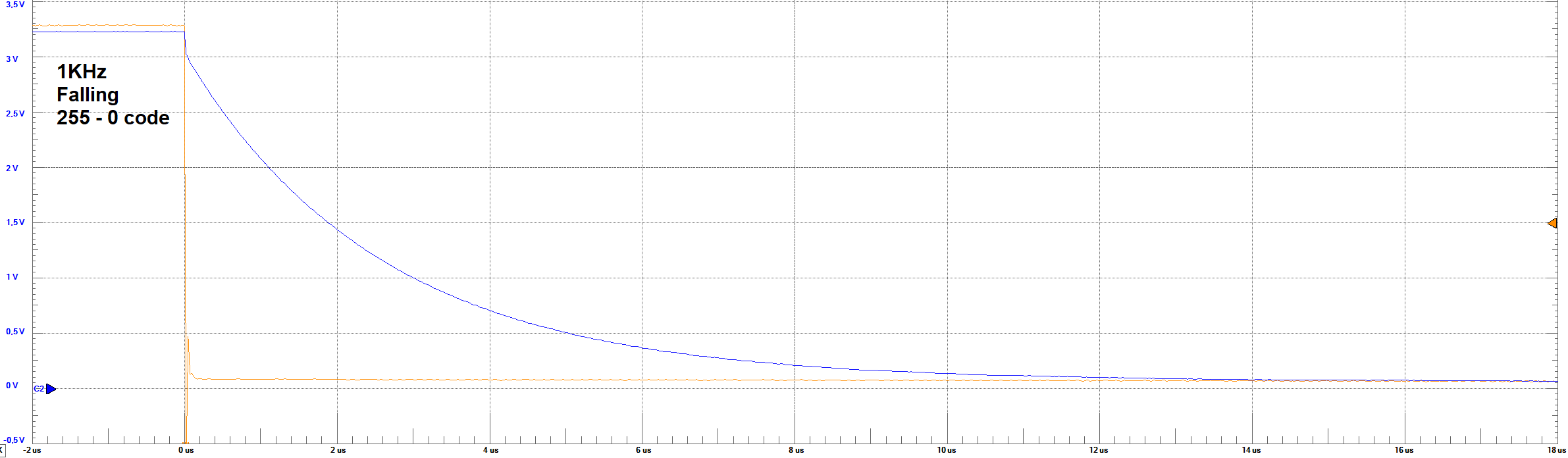
Settling Times - 1 KHz - 255 to 0 code step
The orange line represents the bit 8 of the converter (MSB), and the blue one represents the output analog voltage.
Measurements
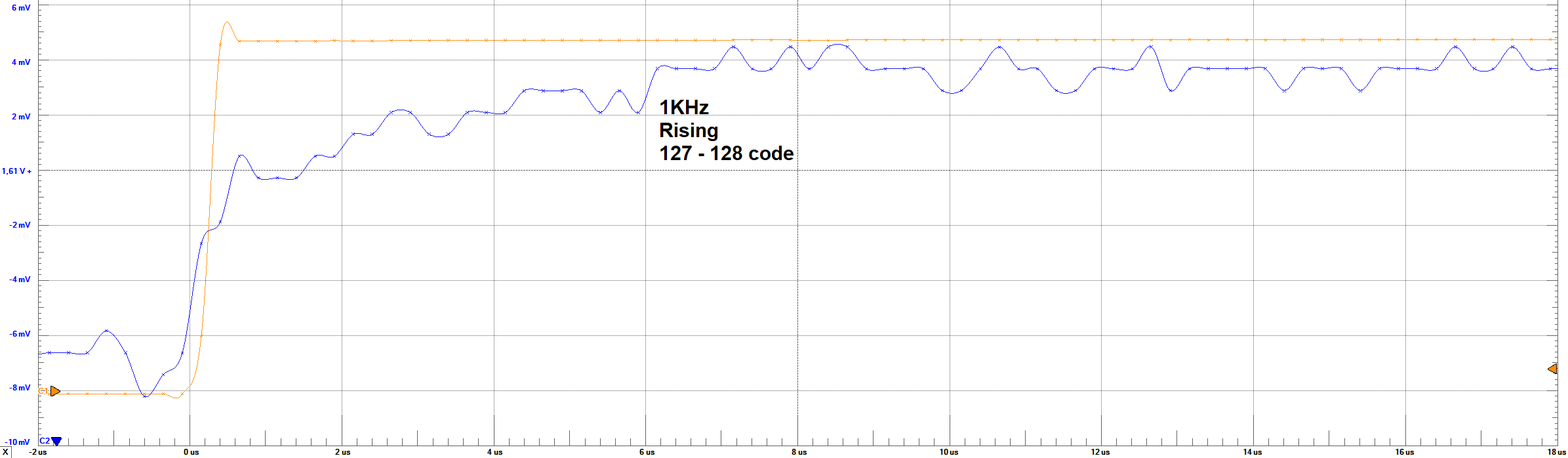
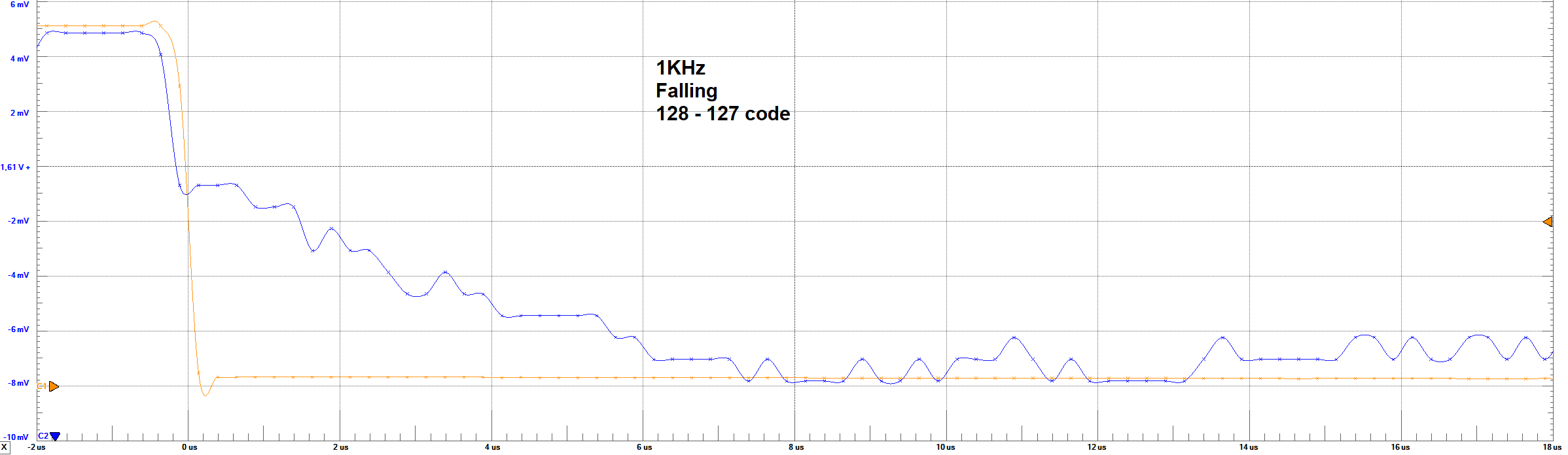
Settling Times - 1 KHz - 127 to 128 code step
The orange line represents the bit 8 of the converter (MSB), and the blue one represents the output analog voltage.
Measurements
Settling Times Analysis
From the images of Settling times, it can be observed the behaviour of the output voltage regarding the change in the full code scale and in
one code step (1 LSB). For the 10KHz frequency, no problem is observed in the waveform. However, for 1 LSB, it was not expected to obtain a big overshoot
in the output. A rough estimation based on the images, give us about 300% overshoot. This behaviour could only be explain by a resonance circuit
formed in the bread-board (Circuit RLC - second order system). For the 100KHz frequency, it can be observed that with this frequency the circuit is
not reaching its steady-state. Therefore, it can be said that the circuit is not capable to respond to this frequency. No settling time could be
measured from this result.
According to the images, the following table resume the times and voltages identified
| Set Parameter | Settling Time Rising Full-Code | Settling Time Rising LSB | Settling Time Falling Full-Code | Settling Time Falling LSB | LSB Voltage | Max Voltage | Min Voltage |
| 1 KHz | ≈ 8 μs | ≈ 6 μs | ≈ 8 μs | ≈ 6 μs | ≈ 11 mV | ≈ 3.1 V | ≈ 50 mV |
| 10 KHz | ≈ 7.8 μs | ≈ 75 ns | ≈ 7.8 μs | ≈ 90 ns | ≈ 14 mV | ≈ 3.15 V | ≈ 50 mV |
From these results, it can be observed that the settling times are simetric in the falling or rising codes. These values were taken measuring
aproximately at which time the signal reaches a steady-state between 95% of the final voltage.
Net step is to measure the DNL and INL of the ramp output. however this is not going to be done for 100KHz frequency as the circuit is not reaching a steady-state,
and therefore lead to more error in the DNL and INL measurement
Measurements
DNL and INL
Following the procedure, the filtered data of a rampwave was introduced to the Data Osc Procesor. From that tool, we can obtain (with apropiated selection of settings) the DNL and INL graphics.
10KHz Parameter
Results for the 10KHz binary output setting.| |
|
| |
|
Measurements
DNL and INL
10KHz Parameter Analysis
Aparently, the transfer chart give us the idea that the behaviour of the ramp is really close to the ideal ramp. However, the zoom area to the origin showed us that the data
points were not so stable for low codes. Also, the INL indicated that at low codes there was a huge amount of error, and for codes grater than 150 the errors are not so big.
As the INL is greater than 1 LSB, is not acceptable performance. the assumption that the parameter of 10KHz was still high enough was made, as for high frequency the output
deformed the ramp at low codes. Perhaps that was happening in this case, but was not observable. The subsequent step was to decrease the frequency parameter (for example: 1KHz).
1KHz Parameter
Results for the 1KHz binary output setting.| |
|
| |
|
Measurements
DNL and INL
1KHz Parameter Analysis
Now the INL and DNL have an acceptable range of error between +/-0.5 LSB, and the samples are better distributed into the steps. It can also be observed some noise over the
samples, but not considerable to damage the performance. The zoom window show also that the lowest codes have negative values, which mean that the minimum voltage is not 0,
and therefore could be an offset-error of -30mV.
Comparing also the DNL and INL graphic with the simulated circuit with the corresponding measured values of resistances, the shape of the waves are very similar,
so it was somehow expected.
Comparison between the measurement and simulated DNL and INL. Left(Measurement) and Right(Simulation)
| |
|
With this behaviour, we can say that the problem here was due to frequency limits rather than the inaccuracy of the resistances. Even with 1% tolerance values, we get values
of INL and DNL between the desired range of +/-0.5 LSB. Therefore is not necesary to improve the circuit by changing resistances.
According to these results, the best frequency operation of the pattern generator is the lowest of the provided set. In this case, I had to do an extra measurement in 1KHz
in order to achieve error results between the desirable range.
Measurements
Bad extraction of rampwave
For the following example, a bad filtering of the data from a rampwave signal was given to the tool. Also, a bad selection of parameters in the tool was selected.
| |
|
| |
|
This was the same data used for the 1KHz analysis. As it can be seen, the wrong filtering of the data, specially on the edges of the rampwave,
summed also with a bad selection of data points for analysis, led to high values of error in DNL and INL graphic. Without knowing that the
input data is bad filtered, would lead to think that the converter has a gain error. A good filtering of the same data, lead to the results for
the 1KHz analysis. There a better performance over the DNL and INL error was obtained.
Measurements
Sine wave input
These are the following measurements made to the circuit.
- Output Voltage for 43 cycles wave
- FFT results
Measurements
Sine wave input
43 Periods SineWave
The file of the digital input of the sine wave was imported to the pattern generator as stated in the instructions.
The following is the FFT calculated from the FFT analysis tool. Before this tool was used, first the data needed to be converted from voltage into codes, in order to use the FFT tool.
Results shows the following information:
| |
|
| |
|
Measurements
Sine wave input
43 Periods SineWave Analysis
As expected, there is a peak at a frequency of 43. The value of the magnitude of this peak is similar to the obtained for the simulated circuit. We also can observe
that there is no reasonable high harmonics over the FFT and the noise level is distributed over a range below -32 dB. That give us the following SNR:
\( SNR = 36.11 {dB} - (-13.82 {dB}) = 49.93{dB} \)
This value is still good, because the theory says that for every bit we need aproximately 6 dB of SNR, and therefore for 8 bit is ≈ 48 dB. Which means we are not
loosing codes and at the same time the ENOB is still 8 bit.
The graphic of the histogram INL and DNL was not expected. It was expected to be more DNL error in the corner codes than in the middle. However, for the measurement is
not distinguishable this behaviour.
Measurements
Sine wave input
Bad Filtering example
For the following example, a sinewave with 11cycles was introduced to the circuit and the output was measured. The data was converted into integers, so the
FFT analysis could be done. the following is the result of bad data filtering.
| |
|
| |
|
From the time data it can be seen that the wave has more than the requiered 11 periods of the signal. For that reason the selected data is not equally distributed over
the range of the codes. The FFT result shows that rather than a pure sine signal, it is more like a sum of harmonics and frequencies near the real frequency. The solution
for this data is to fit the correct data points to form 11 cycles of the signal.
Measurements
Calibration ramp input
For the calibration process, a ramp wave input is introduced to the circuit. The output is measured to generate a lookup table to give better performance in the
INL and DNL parameters of the converter.
Th following image presents the output to the rampwave input.
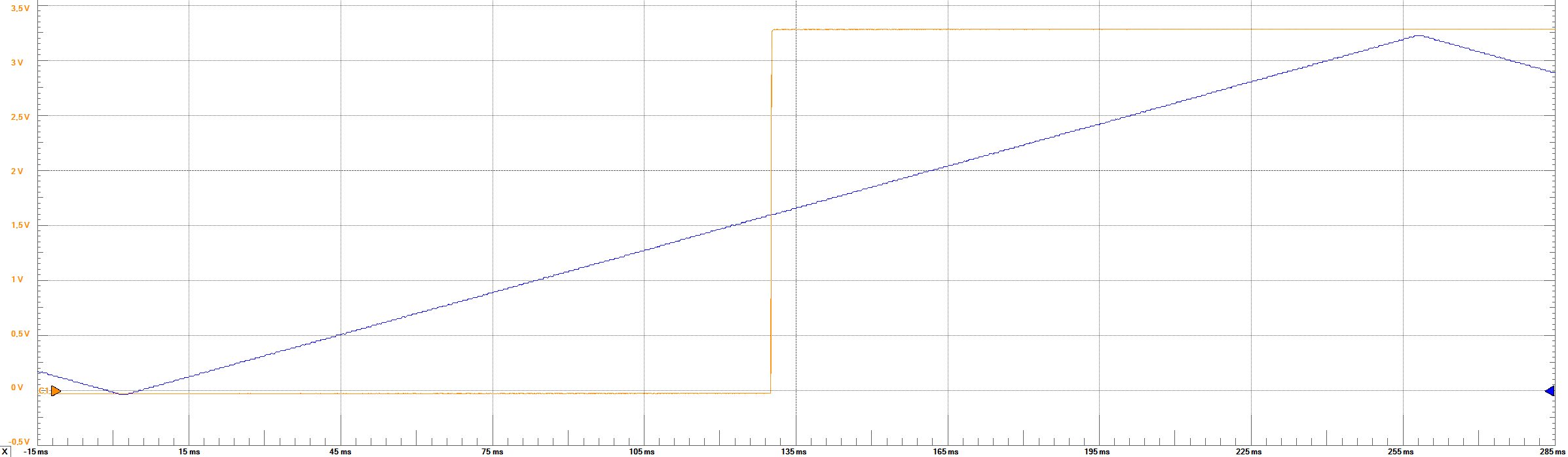 |
Measurements
Calibration Lookup Table
The analysis given by the tool for the rampwave is the following:
| |
|
| |
|
It can be seen that the DNL and INL error magnitude is within +/- 0.5. Using the tool to obtain the calibration codes, it gave
that for the new ramp, 193 codes will be used. These codes were copied into the ramp generation with calibration and
obtained a file that was fed into the pattern generator.
Measurements
Calibration Results
Again a ramp wave was obtained and measured. From the DNL and INL graphic, the codes used in this new ramp are less.
Also, it can not be seen a subtancial improvement in the error magnitude, and in fact it seems that the number of peaks in the error graphic
are more than without calibration.
The analysis of this ramp is the following:
| |
|
| |
|
Measurements
Calibration Results
Using the same lookup table, a sine wave of 11 cycles was used. The following images shows the output, the reading process of the data and the FFT
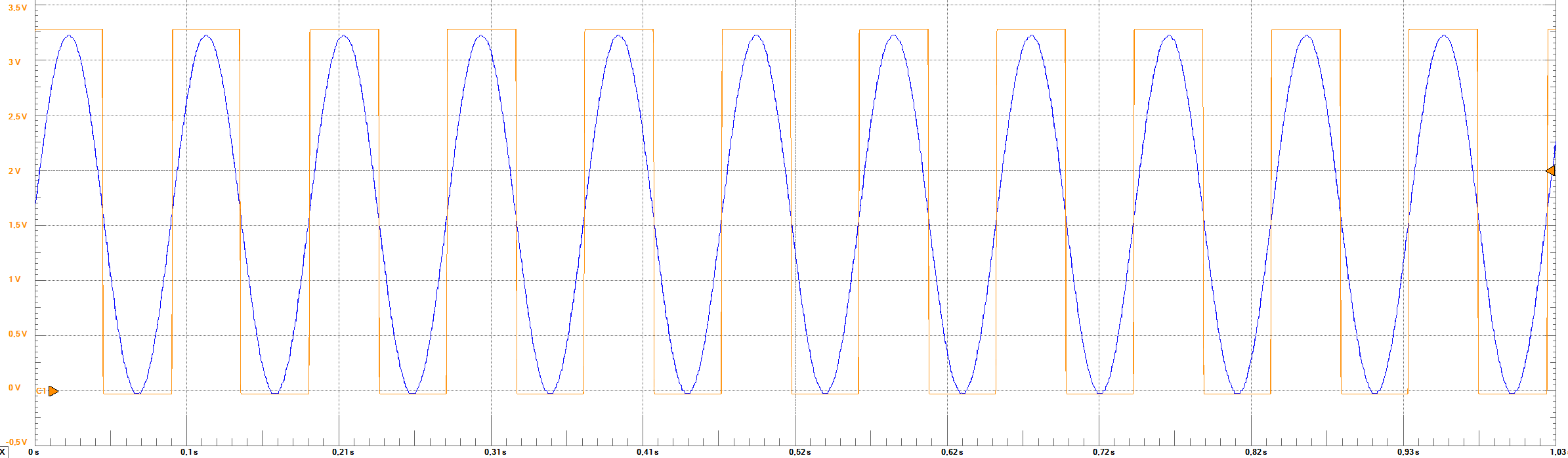
| |
|
| |
|
Measurements
Calibration Results
Using the same lookup table, a sine wave of 43 cycles was used. The following images shows the reading process of the data and the FFT
| |
|
| |
|
Measurements
Calibration Analysis
If we compare the results of these sinewaves with the sinewave of 43 cycles from previous results, there is a slightly deterioration in
the SNR in the center frequency using calibration procedure. Also, the noise floor is distributed over the range of frequency without
presenting harmonics, but the magnitude decrease, which means that the noise is more than without calibration.
It can be concluded that the calibration procedure did not presented an improvement for the circuit, and in fact a worse measurement can be
obtained for different inputs. Therefore, the calibration is not recommended by using this tool.
Converter Implementation problems
- Mainly, the procedure to use the reading and the analysis tools was not so well stablished. Therefore, much time was invested in the process to learn the use
of these tools (Mostly by trial and error method). This was fixed by the professor, uploading graphic content to use them properly. - For some sinewave inputs was difficult to obtain the exact values of the periods within the data output. This led to the "bleeding" error in the FFT analysis.
An easy solution to overcome this problem, is to filter the data to have an exact number of the requiered periods. The parameters in the reading tool need also
to be updated.
Conclusions
- From implementation of the R2R architecture, we can obtain an effective analog value which fullfils an stablished code.
- Though the real converter has an slightly different behaviour, simulation is still a good aproximation, specially with data that aproximates to the real circuit.
- For the circuit behaviour, the bandwidth of the circuit will be limited specially for the pasive elements (resistances, capacitances) bandwidth.
- Despite the fact that the resistances values are not perfect, a tolerance of 1% is enough to obtain a good value. However, a measure shall always be made.
- A suitable range or limit to the circuit was investigated, in order that the following measurements were not affected as a consequence of the previous factor.
- For the ramp wave analysis, is not enough to obtain the ramp wave, as some of the codes output could be missing. All codes shall be tested.
- The DNL and INL give us a better comprehension of the error behaviour, and the graphic could help us to identify errors in the measuring procedure, a big deviation
in the resistance values, or the error of the circuit itself. - The FFT analysis of the sinewave give us a general idea of the response of the circuit in the frequency domain. Indicates how "pure" is the sine wave output through
the harmonics identification. How is the SNR and if it is enough for the usage of all bits (ENOB). How is the noise floor over the range of frequencies. - with the calibration process a worse perfomance of the converter was obtained. However, the results were attached to the functioning of the analysis tools which
in this practice we have not control over it. Perhaps, if we carry out a different analysis on how to obtain the new codes, a better perfomance could be reached. - Knowing the functioning of the analysis tools, as well as the measurement software, is crucial to obtain and correct errors made to the measurement data.
Hochschule für angewandte Wissenschaften Kempten, Jörg Vollrath, Bahnhofstraße 61 · 87435 Kempten
Tel. 0831/25 23-0 · Fax 0831/25 23-104 · E-Mail: joerg.vollrath(at)fh-kempten.de
Impressum