Schaltungstechnik08 StromquellenProf. Dr. Jörg Vollrath06 07 Emitterschaltungs Variationen Elektronik 3 Stromspiegel |

|
Video der 8. Vorlesung 14.4.2021
|
Länge: |
0:2:0 MOSFET als Diodenersatz 0:3:30 Spannungen und Stromgleichung 0:7:15 Kleinsignalersatzschaltbild r = 1/gm 0:12:58 Stromquelle, Stromspiegel 0:15:0 Kennlinie Stromquelle 0:16:50 Ausgangskennlinie 0:20:10 Stromverhältnis 0:22:26 Stromverstärker 0:25:44 Kleinsignalausgangswiderstand 0:29:40 Beispiel mit Zahlen 0:34:50 UGS = 2.1 V 0:38:20 Maximale Abweichung des Stromes 0:44:40 Kleinsignalausgangswiderstand 0:48:35 LTSPICE Verifikation 0:53:55 165 uA 0:55:0 Praktischer Aufbau der Stromeinstellung durch Widerstand 0:59:0 Verstärkerschaltung Rechnung 1:5:15 Vorgehen Lösung |
Rückblick und Übersicht
- Aufgaben: BJT Basischaltung, Sourceschaltung
- MOSFET Sourceschaltung
Heute
- MOSFET als Diodenersatz
- Stromspiegel, Ausgangswiderstand
- Stromspiegel Beispiel
- Stromspiegel als Widerstandsersatz
- Stromspiegel bei Verstärkerschaltungen
- Wilson Stromspiegel
- Strombank
- Referenzspannung und Referenzstrom
MOSFET als Diodenersatz
|
Berechnung der Kennlinie: I = f(U) Kleinsignalausgangsleitwert
Arbeitspunkt: Sättigung \( U_{DS} > U_{GS} - U_{Th} \)
\( I_{DS} = \beta \left( U_{GS} - U_{Th} \right)^{2} \) Quadratische Kennline Kleinsignalausgangsleitwert: \( g_{A} = \frac{d I_{DS}}{d U_{GS}} = 2 \cdot \beta \cdot \left( U_{GS} - U_{Th} \right) = g_{m} \) |
Ein MOSFET bei dem Gate und Drain verbunden sind verhält sich ähnlich, wie eine Diode.
Der Enhancement-Transistor (NMOS: Uth > 0) befindet sich in der Sättigung.
Bei sehr kleinen Spannungen befindet sich der MOSFET im Unterschwellspannungsbereich und hat eine exponentielle Stromkennlinie: IDS ∝ exp(Uth)
Bei großen Strömen wird die Kennlinie quadratisch.
Durch diese Schaltung kann man Dioden und Widerstände ersetzen.
Der Enhancement-Transistor (NMOS: Uth > 0) befindet sich in der Sättigung.
Bei sehr kleinen Spannungen befindet sich der MOSFET im Unterschwellspannungsbereich und hat eine exponentielle Stromkennlinie: IDS ∝ exp(Uth)
Bei großen Strömen wird die Kennlinie quadratisch.
Durch diese Schaltung kann man Dioden und Widerstände ersetzen.
Stromspiegel
|
Einsatz Lastelement anstatt eines Widerstandes Konstantstromquelle
\( I_{DS} = \beta \left( U_{GS} - U_{Th} \right)^{2} \left( 1 + \lambda U_{DS} \right) \)
\( U_{GS1} = U_{GS2} \) \( \frac{I_2}{I_1} = \frac{\beta_2}{\beta_1} \frac{ \left( 1 + \lambda U_{DS2} \right) }{\left( 1 + \lambda U_{DS1} \right)} = \frac{W_2 \cdot L_1 }{W_{1} \cdot L_{2}} \frac{ \left( 1 + \lambda U_{DS2} \right) }{\left( 1 + \lambda U_{DS1} \right)} \) mit \( L_{1} = L_{2} \) \( \frac{I_2}{I_1} \approx \frac{W_{2} }{W_{1}}\) \( \lambda \) ist sehr klein. Man kann mit einem Stromspiegel durch die Wahl eines geeigneten Weitenverhältnisses oder der Anzahl der Transistoren einen Strom verstärken. |
Ausgangswiderstand des Stromspiegels
|
Ausgangswiderstand von M2
\( R_{out} = r_{D} \)
Der Ausgangswiderstand oder Innenwiderstand einer Stromquelle sollte möglichst groß sein MOSFET: \( R_{out} = \frac{1}{I_{DS} \lambda} \) Bipolar: \( R_{out} = \frac{U_{EA}}{I_{C}} \) \( \frac{1}{ \lambda} \) entspricht \( U_{EA} \) |
Beispiel MOS Stromspiegel
|
Berechnen Sie den Strom \( I_2 \) und den Ausgangswiderstand von folgender Schaltung. \( I_{1} = 150 \mu A, V_{DD} = 10 V,\) \( V_{Th} = 1 V, K_{n} = 250 \mu A V^{-2},\) \( \lambda = 0.0133 V^{-1} \)
\( I_{DS} = \frac{K_N}{2} \left( U_{GS} - U_{Th} \right)^{2} \left( 1 + \lambda U_{DS} \right) \)
Zur Berechnung des Arbeitspunktes wird der Term \( 1 + \lambda U_{DS} \) vernachlässigt. \( U_{GS} = U_{Th} + \sqrt{ \frac{2 \cdot I_{1}}{K_N}} = 1V +\sqrt{\frac{2 \cdot 150 \mu A}{250 \mu A V^{-2}}} = 2.1 V \) \( I_2 \) unter Berücksichtigung von \( \lambda \) \( I_{2} = 150 \mu A \frac{1 + \lambda V_{DD}}{1 + \lambda U_{GS}} = 150 \mu A \frac{1 + 0.0133 \cdot 10 }{1 + 0.0133 \cdot 2.1} = 150 \mu A \frac{1.13}{1.028} = 165 \mu A \) Es gibt eine kleine Stromerhöhung (10%) durch die Spannung \( U_{DS} \) von 10V. Ausgangswiderstand: \( R_{out} = \frac{1}{I_{DS} \cdot \lambda } = \frac{1}{165 \mu A \cdot 0.0133 V^{-1}} = 456 k \Omega \) Wollte man den Transistor durch einen ohmschen Widerstand ersetzen, benötigt man folgende Spanung: \( U = I_{2} \cdot R_{out} = 165 \mu A \cdot 456 k \Omega = \frac{1}{\lambda} = 75V \) |
Nachdenken über die Lösung
- Wann kann man \( \left( 1 + \lambda U_{DS} \right) \) vernachlässigen?
- Nicht ideales Spiegelverhältnis
- \( U_{DS} \) ist unterschiedlich
- Ausgangswiderstand
- äquivalente Spannung \( \frac{1}{\lambda } \)
- Typischer Wert \( > 100k \Omega \)
Stromspiegel bei Verstärkerschaltungen
|
Gezeigt ist eine einfache Verstärkerschaltung, wie sie im Praktikum aufgebaut wird.
Eine Wechselspannung am Eingang A wird verstärkt und am Ausgang D kann man eine Wechselspannung mit einer größeren Amplitude beobachten.
Der Transistor M2 ist das verstärkende Bauelement.
Der Drainlastwiderstand wurde durch den Transistor M4 ersetzt, der einen großen Ausgangswiderstand besitzt und eine hohe Verstärkung garantiert.
Die Transistoren M1 und M3 erzeugen eine geeignete Referenzspannung für M4 und bestimmen den Stromverbrauch und den Arbeitspunkt der Schaltung.
Der Widerstand R1 liegt zwischen Ausgang und Eingang und stellt eine geeignete Gate-Source-Gleichspannung für M2 ein.
Die Kapazitäten C1 und C2 stellen für Wechselspannungen einen Kurzschluss dar und blockieren einen Gleichanteil.
Eine Wechselspannung am Eingang A wird verstärkt und am Ausgang D kann man eine Wechselspannung mit einer größeren Amplitude beobachten.
Der Transistor M2 ist das verstärkende Bauelement.
Der Drainlastwiderstand wurde durch den Transistor M4 ersetzt, der einen großen Ausgangswiderstand besitzt und eine hohe Verstärkung garantiert.
Die Transistoren M1 und M3 erzeugen eine geeignete Referenzspannung für M4 und bestimmen den Stromverbrauch und den Arbeitspunkt der Schaltung.
Der Widerstand R1 liegt zwischen Ausgang und Eingang und stellt eine geeignete Gate-Source-Gleichspannung für M2 ein.
Die Kapazitäten C1 und C2 stellen für Wechselspannungen einen Kurzschluss dar und blockieren einen Gleichanteil.
Stromspiegel bei Verstärkerschaltungen: Beispiel
|
\( V_{DD} = 5 V, \lambda = 0.001 V^{-1} \) \( KPN = KPP = 1 mA V^{-2} \) \( V_{Thn} = 1.5 V, V_{Thp} = -1.5 V \) Berechnen Sie die Spannungen am Punkt E und C. Berechnen Sie den Strom IDSM4. Berechnen Sie den Eingangswiderstand und die Spannungsverstärkung
\( V_{DS1} = V_{GS1}, V_{DS3} = V_{GS3}, V_{DD} = V_{GS1} - V_{GS3} \)
\( I_{DS1} = - I_{DS3} \) \( \frac{KPP}{2} \left( V_{GS3} - V_{Thp} \right)^{2} = \frac{KPN}{2} \left( V_{GS1} - V_{Thn} \right)^{2} \) \( V_{GS1} = - V_{GS3} \) \( V_{GS3} = \frac{V_{DD}}{2} = V_{E} = 2.5V \) \( I_{DS1} = \frac{KPN}{2} \left( V_{GS1} - V_{Thn} \right)^{2} = 0.5 mAV^{-2} \left( 2.5 V - 1.5 V \right)^{2} = 0.5 mA \) Stromspiegel: \( I_{DSM4} = I_{DSM3} = - I_{DSM1} = - 0.5 mA \) Spannung an Punkt B: \( I_{DSM4} = I_{DSM2} \), \( V_{B} = \sqrt{I_{DSM2} \frac{2}{KNN}} + V_{Thn} = 2.5V \) Spannung an Punkt C: Gleichspannung: Es fliesst kein Gleichstrom durch den Widerstand R1. \( V_{B} = V_{C} = 2.5 V \) |
Stromspiegel bei Verstärkerschaltungen: Kleinsignalanalyse
|
\( V_{DD} = 5 V, \lambda = 0.001 V^{-1} \) \( KPN = KPP = 1 mA V^{-2} \) \( V_{Thn} = 1.5 V, V_{Thp} = -1.5 V \) Berechnen Sie die Spannungen am Punkt E und C. Berechnen Sie den Strom IDSM4. Berechnen Sie den Eingangswiderstand und die Spannungsverstärkung
\( V_C = V_B = V_E = 2.5 V \), \( I_{DS1} = I_{DS2} = 0.5 mA \)
\( r_{DS2} = r_{DS4} = \frac{1}{I_{DS2} \cdot \lambda} = \frac{1}{0.5 mA \cdot 0.001 V^{-1}} = 2 M \Omega \) gDS = 0.5 µS \( g_{m2} = \frac{2 \cdot I_{DS2}}{ V_{GS2} - V_{Thn}} = \frac{1 mA}{1 V} = 1 mS \) Verstärkung: Stromgleichung \( \frac{v_{GS}-v_{C}}{R1} = g_{m} \cdot v_{GS} + \frac{v_{C}}{r_{DS2}||r_{DS4}||r_{2}} \) \( r = r_{DS2}||r_{DS4}||r_{2} = 90.1 k \Omega \) \( v_{GS} \left( \frac{1}{R_{1}} - g_{m} \right) = v_{C} \left( \frac{1}{r} + \frac{1}{R_{1}} \right) \) \( \frac{v_{C}}{v_{GS}} = \frac{1 - R_{1} \cdot g_m }{1 + \frac{R_{1}}{r}} \) \( \frac{v_{C}}{v_{GS}} = \frac{1 - 1M\Omega \cdot 1 mS }{1 + \frac{1 M\Omega}{90.1k}} = -82.57 \) Eingangswiderstand: \( v_{GS} = i \cdot R_1 + \left( i - g_m \cdot v_{GS} \right) \left( r_{DS2} || r_{DS4} || R_{2}\right)\) \( v_{GS} \left( 1 + g_m \cdot \left( r_{DS2} || r_{DS4} || R_{2}\right) \right) = i \cdot \left( R_1 + \left( r_{DS2} || r_{DS4} || R_{2}\right) \right)\) \( r_{i} = \frac{v_{GS}}{i} = \frac{R1 + \left( r_{DS2}|| r_{DS4} || r_{2}\right)} { 1 + g_m \left( r_{DS2}|| r_{DS4} || r_{2} \right)} = \frac{ 1M + 90.1 k}{1 + 1m \cdot 90.1 k} \Omega = 11.9 k\Omega \) |
Nachdenken über die Lösung
- Der Arbeitspunkt wird über den Strom des Stromspiegels bestimmt, dafür wird der Eingangswiderstand kleiner.
- Kleines \( \lambda = 0.001 V^{-1} \rightarrow \) großes \( r_{DS} \).
- Eingangswiderstand:
\( r_{i} = \frac{v_{GS}}{i} = \frac{R1 + \left( r_{DS2}|| r_{DS4} || r_{2}\right)} { 1 + g_m \left( r_{DS2}|| r_{DS4} || r_{2} \right)} = \frac{ 1M + 90.1 k}{1 + 1m \cdot 90.1 k} \Omega = 11.9 k\Omega \)
- Wenn die Lastwiderstände \(r_{DS}, R_{2} \) größer werden, wird auch der Eingangswiderstand größer.
- Verstärkung:
\( \frac{v_{C}}{v_{GS}} = \frac{1 - R_{1} \cdot g_m }{1 + \frac{R_{1}}{r}} \)
\( \frac{v_{C}}{v_{GS}} = \frac{1 - 1M\Omega \cdot 1 mS }{1 + \frac{1 M\Omega}{90.1k}} = -82.57 \)- Wenn die Lastwiderstände \(r_{DS}, R_{2} \) größer werden, wird auch die Verstärkung größer.
Simulation mit LTSPICE
Aufbau und Messung: Praktikumsversuch
Alle Bauteile werden gesetzt und alle Verbindungen hergestellt: Liste abhaken.
Spannungsversorgung anlegen. Gemessenen Stromverbrauch und Großsignalarbeitspunkt mit berechneten Werten vergleichen.
Wechselspannungssignal anlegen und Verstärkung messen.
Wilson Stromspiegel
|
\( I_3 = I_{DS3} = I_{DS1} \),
\( I_{REF} = I_{DS2} \)
\( \frac{I_{DS1}}{I_{DS2}} = \frac{ 1 + \lambda \cdot V_{GS}}{1 + \lambda \cdot 2 \cdot V_{GS}} \) Wilson Stromspiegel: \( I_{DS3} = I_{DS1} = I_{DS2} \frac{ 1 + \lambda \cdot V_{GS}}{1 + \lambda \cdot 2 \cdot V_{GS}} \) Einfacher Stromspigel: \( I_{DS4} = I_{REF2} \left( 1 + \lambda \cdot V_{DS4} \right) \) 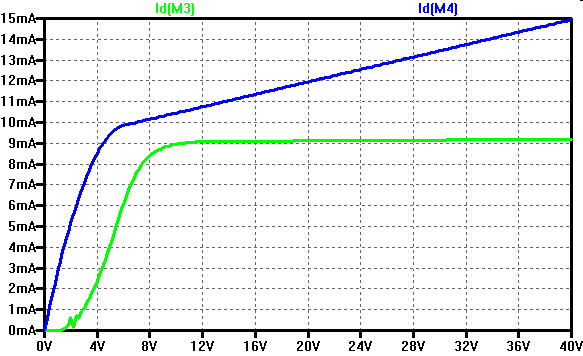 Die geringe Steigung bedeutet ein hoher Ausgangswiderstand der Stromquelle. Erst ab einer höheren Ausgangsspannung funktioniert die Stromquelle. |
Die Transistoranordnung des Wilson Stromspiegels ist eine Kaskode.
Das Wort Kaskode ist ein Kofferwort und setzt sich aus den beiden Begriffen „Kaskadierte Kathoden“ zusammen, was die Reihenschaltung der beiden Kathoden bei den ursprünglich eingesetzten Elektronenröhren andeuten soll. Quelle: Wikipedia
Das Wort Kaskode ist ein Kofferwort und setzt sich aus den beiden Begriffen „Kaskadierte Kathoden“ zusammen, was die Reihenschaltung der beiden Kathoden bei den ursprünglich eingesetzten Elektronenröhren andeuten soll. Quelle: Wikipedia
Wilson Stromspiegel KESB Ausgangswiderstand
|
\( I_{B3} = g_{m3} \cdot u_{gs3} = g_{m3} \cdot ( u_{g3} - u_{g2} ) \)
\( I_{B2} = g_{m2} \cdot u_{gs2} \) \( R_{out} = \frac{u_x}{i_x} \) \( u_{x} = u_{RDSM3} + u_{RM1} = (i_x - g_{m3} u_{gs3}) \cdot r_{DSM3} + i_x \cdot r_{M1} \) \( u_{gs3} = u_{g3} - u_{g2} \) \( u_{g3} = - g_{m2} r_{DSM2} u_{g2} \) \( u_{g2} = \frac{i_x}{g_{m1}} \) \( u_{gs3} = - (1 + g_{m2} r_{DSM2} ) u_{g2} = - (1 + g_{m2} r_{DSM2} ) \frac{i_x}{g_{m1}} \) \( u_{x} = i_x ( 1 + \frac{g_{m3}}{g_{m1}} (1 + g_{m2} r_{DSM2} )) \cdot r_{DSM3} + i_x \cdot r_{M1} \) \( \frac{u_{x}}{i_x} = ( 1 + \frac{g_{m3}}{g_{m1}} (1 + g_{m2} r_{DSM2} )) \cdot r_{DSM3} + r_{M1} \) |
Strombank
LTSPICE Transistormodell mit 4 Anschlüssen:
W, L: Eingabe der Weite und Länge des Transistors
m: Anzahl Paralleltransistoren
Eingabe der Flächen von Drain und Source zur Kapazitätsberechnung.
Da kein Gatestrom fliesst können sehr viele Transistoren verbunden werden.
Besser als Bipolartransistoren.
Referenzstromquellen
- Ein Widerstand oder 2 Transistoren bestimmen den Strom
- Rechts: Versorgungsspannungsunabhängig
- Spannungs- und Temperaturunabhängig: Bandgap Referenz
Zusammenfassung und nächste Vorlesung
- Stromquellen und Stromspiegel