Schaltungstechnik

09 Differenzverstärker

Prof. Dr. Jörg Vollrath

08 Stromquellen

Elektronik 3 Stromspiegel

Video der 9. Vorlesung 20.4.2021

Länge: 1:15:41

0:04:00 Beispiel Verstärker mit Stromspiegel

0:05:00 Kleinsignalersatzschaltbild

0:08:28 Miller Rin, Rout

0:12:55 Diskussion Spannungsverstärkung

0:20:25 Aufgabe zu Hause Wilson Stromspiegel

0:23:25 Strombank

0:24:25 Referenzstromquellen

0:26:21 Differenzverstärker

0:27:23 Gleichtakt-, Störsignalunterdrückung

0:29:8 Schaltbild mit Stromspiegel und Erklärung

0:35:45 Gegentakt und Gleichtakt

0:42:45 Differenzverstärkung

0:45:20 KESB Zeichnung

0:50:35 Rechnung

1:00:15 Gleichtaktverstärkung

1:01:53 KESB Zeichnung

1:05:38 Rechnung

Rückblick und Übersicht

MOSFET als Diodenersatz
Stromspiegel, Ausgangswiderstand
Stromspiegel Beispiel
Stromspiegel als Widerstandsersatz
Stromspiegel bei Verstärkerschaltungen
Wilson Stromspiegel
Strombank
Referenzspannung und Referenzstrom

Heute

Der Differenzverstärker ist die Basis für den Operationsverstärker
Schaltung
Symmetrie, gleiche Transistoren, integrierte Schaltungen
2 Eingänge, Gleichspannungsgekoppelt
Gleichanteil, Differenzanteil
Eingangswiderstand, Ausgangswiderstand, Verstärkung

Schaltbild

Stromquelle M6 (NFET)
Stromspiegel M4, M5 (PFET)
Eingangstransistoren M2, M7 (NFET)
Gleiche Transistorpaare

M2, M7
M4, M5

Eingang: VA, VB
Ausgang: OUT

Arbeitspunkt: Stromquelle M6
Symmetrische Sourceschaltung

Der Strom verteilt sich hälftig auf M2 und M7

Der zweite Eingang des Differenzverstärkers erlaubt die Messung von Differenzen.
Schwankungen der Versorgungsspannung zeigen sich am Ausgang kaum.

Gegentakt, Differenzverstärker, Signale

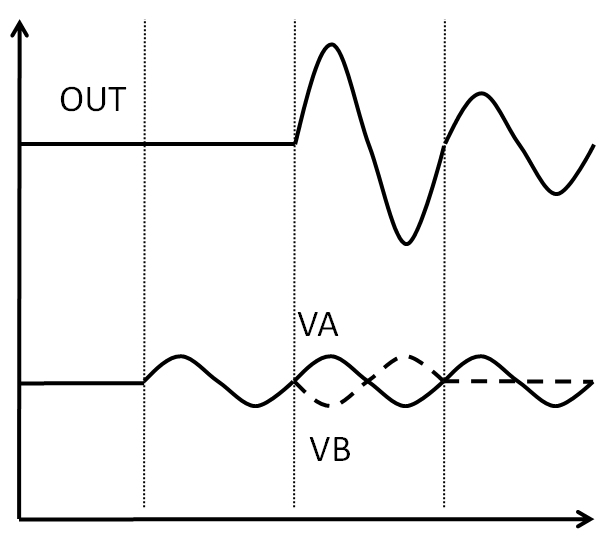
Eingangssignal:

Gleichtakt: \( u_{gl} = \frac{u_A + u_B }{2} \)

Gegentakt, Differenz: \( u_D = u_A - u_B \)

Direkte Einkopplung, keine Koppelkapazität, Gleichspannungsverstärkung
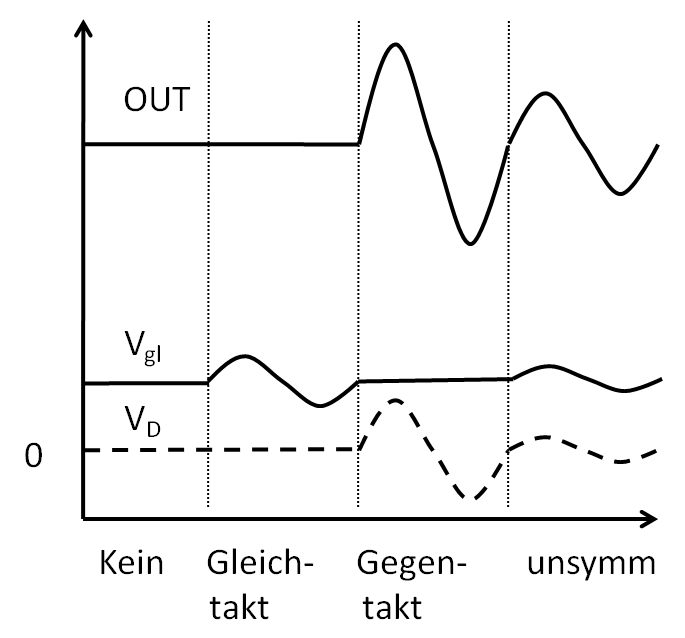
Bei 2 Eingängen kann man das Eingangssignal in einen Gleichtaktsignal und ein Gegentaktsignal zerlegen.
Idealerweise hat der Verstärker eine große Gegentaktverstärkung und keine Gleichtaktverstärkung.
Idealerweise wirkt sich eine Versorgungsspannungsänderung nicht auf das Ausgangssignal aus.
Im Allgemeinen spricht man von single ended und differentiellen (differential) Signalen.
Differentielle Signale sind nicht so störanfällig, da sich Störungen auf beide Signalleitungen auswirken und nachfolgende Differenzverstärker mit geringer Gleichtaktverstärkung diese Störungen unterdrücken.

Funktionsweise des Differenzverstärkers

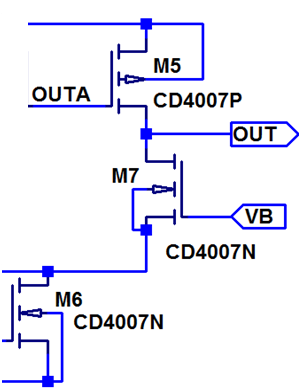
M6 ist ein Stromspiegeltransistor und stellt den Arbeitspunkt der Schaltung I_DS ein.
Mit I_DS wird über g_m und r_D die Verstärkung und die Leistungsaufnahme festgelegt.

u_a liegt am positiven Eingang
Eine Änderung von u_a bewirkt eine Änderung von der Spannung outa, die die Sourceschaltung aus M5 (Verstärker) und M7 (Last) ansteuert.
Eine positive Änderung von u_a bewirkt eine positive Änderung der Ausgangsspannnung.
u_b liegt am negativem Eingang, an der Sourceschaltung aus M7 (Verstärker) und M5 (Last).
Am Ausgang ergibt sich dadurch die verstärkte Differenzspannung:
u_D = k ( u_a - u_b)

Es wird als nächstes das Kleinsignalersatzschaltbild erstellt und die Gegentakt- und Gleichtaktverstärkung berechnet.

Gegentakt- oder Differenzverstärkung v_D KESB

Das Bild zeigt das Kleinsignalersatzschaltbild in LTSPICE.

\( u_{out} \approx \left( u_{a} - u_{b} \right) \frac{ r_{d7} \cdot g_{m7} }{2} \)

Berechnung der Differenzverstärkung:

\( u_{out} = - \left( i_5 + i_7 \right) \cdot \left( r_{d5} || r_{d7} \right) \)
\( u_{out} = - \left( u_{outa} \cdot g_{m5} + u_{b} \cdot g_{m7} \right) \cdot \left( r_{d5} || r_{d7} \right) \)
\( u_{out} = - \left( - u_{a} \cdot g_{m2} \left( r_{D2} || r_{m4} \right) \cdot g_{m5} + u_{b} \cdot g_{m7} \right) \cdot \left( r_{d5} || r_{d7} \right) \)

Näherung \( r_{m4} \ll r_{D2} \)

\( u_{out} \approx - \left( - u_{a} \cdot g_{m2} \frac{g_{m5}}{g_{m4}} + u_{b} \cdot g_{m7} \right) \cdot \left( r_{d5} || r_{d7} \right) \)
Mit \( g_{m5} = g_{m4} \) und \( g_{m7} = g_{m2} \) und \( r_{d5} = r_{d7} \)
\( u_{out} \approx \left( u_{a} - u_{b} \right) \frac{ r_{d7} \cdot g_{m7} }{2} \)

Bei der Differenzverstärkung ist Δ U_A = - Δ U_B und Δ I_A = - Δ I_B. Damit bleibt der Knoten V_low auf konstanten Potential und M6 kann im Kleinsignalersatzschaltbild wegfallen.

Gleichtaktverstärkung: v_Gl mit M6

UDSM6 ändert sich:

M6 Ausgangswiderstand

Man könnte 2 Teilrechnungen betrachten:
- Rechter Zweig der Schaltung: M6, M7, M5 mit Eingangsspannung v_B und fester Spannung u_OUTA
- Linker Zweig der Schaltung: M6, M2, M4 mit Eingangsspannung v_A und Ausgangsspannung u_OUTA
- Aus Symmetriegründen sollte outA = out sein.

1. Rechnung mit Spannungen und Strömen rechter Zweig

\( v_{Gl} = \frac{v_{out}}{v_{B}} = \frac{I \cdot r_{D5}}{v_{GS7} - I \cdot 2 \cdot r_{D6}} = = \frac{1}{\frac{v_{GS7}}{I \cdot r_{D5}} - 2 \frac{r_{D6}}{r_{D5}}} \)
\( I = - g_m \cdot v_{GS7} \frac{r_{D7}||\left( r_{D5} + 2 \cdot r_{D6}\right)}{r_{D5} + 2 \cdot r_{D6}}\)
\( v_{Gl} = - \frac{1}{\frac{r_{D5} + 2 \cdot r_{D6}}{g_m \cdot \left( r_{D5} r_{D7}||\left( r_{D5} + 2 \cdot r_{D6}\right) \right)} + 2 \frac{r_{D6}}{r_{D5}}} \)
\( v_{Gl} = - \frac{1}{\frac{r_{D5} + 2 \cdot r_{D6} + r_{D7}}{g_m \cdot r_{D5} \cdot r_{D7} } + 2 \frac{r_{D6}}{r_{D5}}} \)
\( v_{Gl} = - \frac{r_{D5}}{2 \cdot r_{D6}} \frac{1}{1 + \frac{r_{D5} + 2 \cdot r_{D6} + r_{D7}}{2 \cdot g_m \cdot r_{D6} \cdot r_{D7} }} \approx - \frac{r_{D5}}{2 \cdot r_{D6}} \)

\( v_{Gl} = - \frac{r_{D5}}{2 \cdot r_{D6}} \)

Mit M6 kann man die Gleichtaktverstärkung klein halten.
Störsignale auf beiden Eingängen A und B erscheinen nicht am Ausgang und werden unterdrückt.

Gleichtaktverstärkung (1): v_Gl mit M6 rechter Zweig

Rechter Zweig mit M6, M7, M5 mit Eingangsspannung v_B

\( \frac{u_{out}}{u_{B}} \approx - \frac{ r_{D5} } { 2 \cdot r_{D6}} \)

Kleinsignalersatzschaltbild

M6 wird durch 2 rD6 ersetzt
In einer Schaltungshälfte fliesst der halbe Strom
M7 wird durch die gesteuerte Quelle B7 und den Ausgangswiderstand rD7 ersetzt
M5 wird durch rD5 ersetzt
Zur Berechnung der Spannungsverstärkung interessiert nur der Strom durch rD5 (Stromteiler).
Die gesteuerte Quelle B7 und rD7 wird durch B71 ersetzt, wobei gm durch gmx ersetzt wird.
Die Spannung ui setzt sich aus uGS7 und der Spannung an rD6 zusammen

\( i_{x} = i \frac{r_{D7} || (2 r_{D6} + r_{D5})} {2 r_{D6} + r_{D5}} \)
\( g_{mx} = g_{m} \frac{r_{D7} || (2 r_{D6} + r_{D5})} {2 r_{D6} + r_{D5}} \)
\( u_{out} = - g_{mx} \cdot r_{D5} \cdot u_{GS7} \)
\( u_{B} = u_{GS7} \left( 1 + g_{mx} \cdot 2 \cdot r_{D6} \right) \)
\( \frac{u_{out}}{u_{B}} = - \frac{ g_{mx} \cdot r_{D5} } { 1 + g_{mx} \cdot 2 \cdot r_{D6}} \approx - \frac{ r_{D5} } { 2 \cdot r_{D6}} \)

\( g_{m} = \sqrt{ 2 \cdot KP \cdot I_{DS}} \)
\( r_{D} = \frac{ 1 }{ \lambda I_{DS} } \)

\( r_{D6} = \frac{r_{D5}}{2} \)

Gleichtaktverstärkung (2): v_Gl mit M6 linker Zweig

Linker Zweig mit M6, M2, M4 mit Eingangsspannung v_A

\( \frac{u_{outa}}{u_{a}} \approx - \frac{ r_{m4} } { 2 \cdot r_{D6}} \)

Kleinsignalersatzschaltbild

M6 wird durch 2 rD6 ersetzt
In einer Schaltungshälfte fliesst der halbe Strom
M2 wird durch die gesteuerte Quelle B2 und den Ausgangswiderstand rD2 ersetzt
M4 wird durch gm4 ersetzt
Zur Berechnung der Spannungsverstärkung interessiert nur der Strom durch gm4 (Stromteiler).
Die gesteuerte Quelle B2 und rD2 wird durch B21 ersetzt, wobei gm2 durch gmx ersetzt wird.

\( i_{x} = i \frac{r_{D2} || (2 r_{D6} + r_{m4})} {2 r_{D6} + r_{m4}} \)
\( g_{mx} = g_{m} \frac{r_{D2} || (2 r_{D6} + r_{m4})} {2 r_{D6} + r_{m4}} \)
\( u_{out} = - g_{mx} \cdot r_{m4} \cdot u_{GS7} \)
\( u_{a} = u_{GS2} \left( 1 + g_{mx} \cdot 2 \cdot r_{D6} \right) \)
\( \frac{u_{out}}{u_{a}} = - \frac{ g_{mx} \cdot r_{m4} } { 1 + g_{mx} \cdot 2 \cdot r_{D6}} \approx - \frac{ r_{m4} } { 2 \cdot r_{D6}} \)

\( g_{m} = \sqrt{ 2 \cdot KP \cdot I_{DS}} \)
\( r_{D} = \frac{ 1 }{ \lambda I_{DS} } \)

\( r_{D6} = \frac{r_{D5}}{2} \)

Gleichtaktverstärkung: v_Gl (Baker)

v_a = v_b
i_d fliesst durch M2 und M7
2 i_d fliesst durch M6

v_a = v_gs2 + 2 i_d r_d6 = v_gs7 + 2 i_d r_d6

\( v_{gs2} = \frac{i_{d}}{g_{m2}} \)

\( v_{a} = i_{d} (\frac{1}{g_{m2}} + 2 r_{d6} ) \approx i_{d} \cdot 2 \cdot r_{d6} \)

Symmetrie

\( v_{out} = v_{outa} = - i_{d} \frac{1}{g_{m4}} = - i_{d} \frac{1}{g_{m5}} \)

Gleichtaktverstärkung: v_Gl

\( v_{Gl} = \frac{vout}{va} = \frac{- i_{d} \frac{1}{g_{m4}}}{i_{d} \cdot 2 \cdot r_{d6}} = - \frac{1}{ 2 g_{m4} r_{d6}} \)

Gleichtaktunterdrückung

Common mode rejection rate (CMRR)
Angabe in Dezibel (dB)
\( G = \frac{| v_{D} |}{|v_{Gl}|} = \frac{\frac{g_{m7} r_{D7}}{2}} { \frac{1}{2 \cdot g_{m4} \cdot r_{D6}}} = g_{m7} \cdot r_{D7} \cdot 2 \cdot g_{m4} \cdot r_{D6} \)
\( CMRR = 20 log G \)

Power supply rejection ratio (PSRR)

Änderung des Ausgangssignals bei Spannungsversorgungsänderung

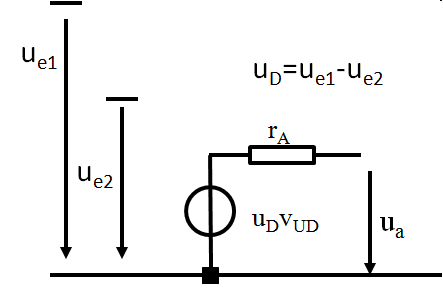
Eingangswiderstand, Ausgangswiderstand, ESB

MOSFET

Eingangswiderstand: \( \infty \)
Ausgangswiderstand \( r_{D5}||r_{D7} \)
Gleichtaktverstärkung: 0

u_e1: positiver Eingang
u_e2: negativer Eingang
u_D: Differenzspannung
v_UD: Differenzspannungsverstärkung

Aussteuerbereich

Gleichtakt
Minimale und maximale Gleichtaktspannung am Eingang
Minimum

M2, M7, M6 in Sättigung
\( V_{DS6} > V_{GS6} - V_{thn} \)
\( V_{GS2} > V_{GS6} - V_{thn} \)

Maximum

M4 in Sättigung

Gegentakt
Ausgangsspannung noch ein Sinussignal
Versorgungsspannung

Simulation Aussteuerbereich

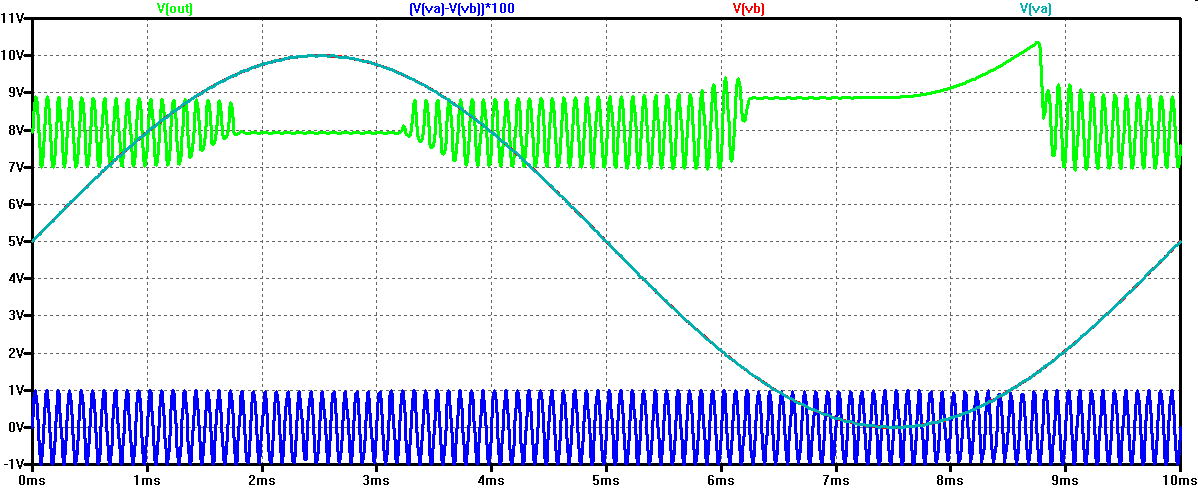
An B liegt eine Sinusspannung mit Offset 5 V und 5 V Amplitude.
An A liegt zusätzlich zu dieser Sinusspannung eine kleines Sinussignal mit 10 mV und einer höheren Frequenz an.

Für Gleichtakt Eingangsspannungen oberhalb von ca. 8.5 V und unterhalb von 2 V funktioniert die Differenzverstärkung nicht und eine konstante Ausgangsspannung ist sichtbar.
Ansonsten wird die Eingangsamplitude von 10 mV auf eine Amplitude von ca. 1 V verstärkt.

Rechnung:

    IDS = 350E-6 A, KPP=1.123E-3, KPN=1.123E-3
    lambda = 0.018, 
     rd7 = 1/(lambda * IDS / 2) =  31.7 u Ohm
     rd5 = rd7
     gm7 = sqrt(2 * KPP * IDS / 2) = 0.63 mS
     gm5 = gm7
     vdiff = rd7 * gm7 / 2 = 99
     vdiff = 20 * log10(vdiff) = 40 dB
   LTSPICE Vgl - 46 dB = 1/200 = 5m
     rd6 = rd5 / 2 
     vgl = - rd5 / 2 / rd6 = - 1
     vgl1 = - 1 /gm5 / 2 / rd6 = 0.005
     vgl1dB = 20 * log10( vgl1) = -46 dB

Variationen:
Gegentakt AC Simulation ergibt 40 dB
Gleichtakt AC Simulation mit VB AC 1 ergibt -46 dB
Bei der Gleichtaktsimulation wird nicht rD5 sondern gm5 wirksam.

Differenzverstärker Beispiel: Arbeitspunkt

\( I_{DS6} = 250 \mu A, Kpn = 250 \mu AV^{-2}, Kpp = 200 \mu AV^{-2}, \)
\( V_{thn} = - V_{thp} = 0.75 V, V_{DD} = 10 V, \)
\( \lambda = 0.0133 V^{-1}, VA = VB = 5 V. \)

Berechnen Sie den Arbeitspunkt.
Berechnen Sie den Übertragungsleitwert, den Ausgangswiderstand und die Spannungsverstärkung.
Wie groß ist der Aussteuerbereich?

Differenzverstärker Nachdenken über die Lösung

Welche Probleme hatten Sie?

Sättigungsgleichung

Kleinsignalersatzschaltbild

Spannungsumlauf, \( R = \frac{U}{I} \)

Lösung

Ergebnisverifikation mit LTSPICE

V_OUT = 8.13 V
V1 = 3.25V
Verstärkung:
u_in = 5 mV
u_out = 8.55 V - 8.13 V = 0.42 V
|v_u| = 80
Simulation Cmd: DC Transfer
--- Transfer Function ---

Transfer_function: 80.7305 transfer
v1#Input_impedance: 1e+020 impedance
output_impedance_at_V(out): 315150 impedanc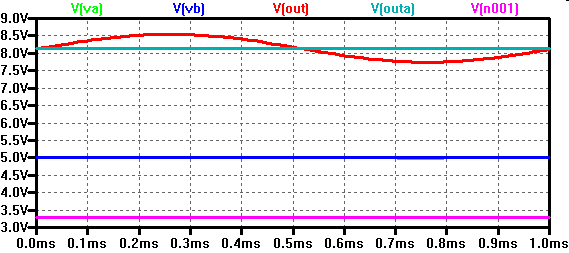

Im Bild wird eine transiente Simulation über die Zeit von 1 ms gezeigt.
Der Operationsverstärker hat am Ausgang für 0 V Differenzspannung einen Offset von 8.0V.
Wie in der nächsten Vorlesung gezeigt kann man diesen Pegel mit einer 2.Verstärkerstufe auf einen geeigneten Wert setzen.

Zusammenfassung und nächste Vorlesung

Differenzverstärker
CMRR
PSRR

Nächstes Mal

10 Operationsverstärker

Literatur

CMOS Circuit Design, Layout and Simulation, Baker, Wiley
CMOS Analog Circuit Design, Allen, Holberg, Oxford
Microelectronic Circuit Design, Jaeger, Blalock
Microelectronic Circuits, Sedra, Smith, Oxford

2021 Schaltungstechnik 09 Differenzverstärker Prof. Dr. Joerg Vollrath