Elektronik 3

04 pn-Übergang

Prof. Dr. Jörg Vollrath

03 Halbleiter

Länge: 00:42:10

0:0:0 Oszilloskop XY Diodenkennlinie

0:0:50 Oszilloskop Trigger

0:2:27 Strommessung mit Widerstand

0:4:9 Add XY

0:6:38 Mitschrift Notizen

0:7:42 Leuchtdiode

0:8:14 Eindimensionaler pn Übergang

0:11:34 Poissongleichung Ladungsträger, Feld und Potential

0:13:58 Transportgleichung, Kontinuitätsgleichung

0:14:56 Sperrschichtdicke

0:16:23 Diffusionsspannung

0:20:8 Beispiel Berechnung Diffusionsspannung und Sperrschichtdicke

0:22:18 Math Notepad zur Berechnung

0:26:5 k Boltzmannkonstante

0:27:15 Diffusionsspannung 0.6..1.1 V, Sperrschichtdicke

0:29:10 Höhere Dotierstoffkonzentration kleinere Raumladungszone

0:29:50 Raumladungszone mit externer Spannung

0:31:30 Animation Diodenverhalten Kennlinie, Ladungsträger

0:35:1 Diodengleichung und Kennlinie

0:37:20 Diodenparameter Is, n

0:38:0 Lineare und logarithmische Darstellung

0:42:10 Formula E

Rückblick und Ausblick

Was ist Störstellenerschöpfung?
Welche Dotierstoffkonzentrationen treten bei Halbleitern auf?
Was ist Rekombination und Generation?
Welche Ladungsträgertransportströme gibt es und wodurch entstehen Sie?
Wie ändern sich die Eigenschaften eines Halbleiters mit der Temperatur?
Warum interessiert uns das Temperaturverhalten von elektrischen Schaltungen?
Was ist ein Devicesimulator und was kann man damit tun?

Heute:

Der pn-Übergang, die Diode

Elektronische Schaltungstechnik, Reinhold: Kapitel 3, S. 41-64
Microelectronic, Jaeger: Chapter 3, page: 75-133

LED

Quelle: Joerg Vollrath

Die Diode wird mit einem 10kΩ Widerstand verbunden und mit einem Sinussignal mit einer Frequenz von 0.5 Hz und einer 8 V Amplitude betrieben (Imax = 8 V / 10 10kΩ = 0.8 mA. Der kleine Halbleiterblock im Inneren leuchtet bei Stromfluss. Der Halbleiterquader ist in einem Kelch aufgeklebt und auf der anderen Seite mit einem Draht verbunden.
Die Elektronik (Halbleiterblock) ist viel kleiner als die Mechanik (Anschlussdrähte, transparentes Gehäuse).

Fragen

Was passiert, wenn ein n-dotierter und p-dotierter Halbleiter in Kontakt treten?

Ladungsträgerkonzentration, elektrisches Feld, Potenzial, Spannung und Strom

Wie sieht die statische Diodenkennlinie aus?

Strom-Spannungskennlinie, Temperaturverhalten
Analytische Gleichung
SPICE Modell

Wie verhält sich die Diode dynamisch?

Kleinsignalverhalten
Schaltverhalten

Was für Diodentypen gibt es?

Ein pn-Übergang: Diode

pn Übergang

Diffusionsstrom
Driftstrom
Raumladungszone

Strom Spannungs Kennlinie

Vorwärts und Rückwärtsbetrieb
Temperaturabhängigkeiten
Durchbruch

Dynamisches Verhalten
Modelle und Ersatzschaltbilder

Mathematisches Modell
SPICE Modell

Gross und Kleinsignalanalyse
Diodentypen:

Shottky-Diode, Zener-Diode, Kapazitätsdiode, Solarzellen,
LED

Diodenschaltungen

Gleichrichter
Spannungsstabilisatoren

Ein pn-Übergang eindimensional (1)

Ein p- und ein n-Halbleiter grenzen aneinander:

pn-Übergang

Schaltsymbol
Wirkprinzip

Ladungsträgerdichte
Diffusionstrom
Ladungsdichte
Driftstrom

Es liegt keine äußere Spannung an.

Anode: p-dotiert z.B. Bor
Kathode: n-dotiert, z.B. Phosphor

Version 4
SHEET 1 880 680
SYMBOL diode 32 32 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName D1
SYMATTR Value ""
TEXT 24 72 Left 2 !Anode
TEXT -50 72 Left 2 !Kathode

Ein intrinsischer Halbleiter

2 dotierte Halbleiter: n- und p-dotiertes Gebiet (N_D, N_A)

Diode: 2 dotierte Halbleiter im Kontakt: n- und p-dotiertes Gebiet

Quelle: Vollrath

Ein intrinsischer Halbleiter hat keine Dotierung. Die Eigenleitungsladungsträger stehen für die Leitung zur Verfügung.
Bringt man einen n- und p-dotierten Halbleiter in Kontakt, diffundieren die beweglichen Ladungsträger entlang des Konzentrationsgradienten. Feste Ladungen bleiben zurück, die ein elektrische Feld erzeugen.
Im Gleichgewicht sind der Driftstrom (Ladung, Feld) und der Diffusionsstrom (Konzentrationsgradienten) gleich gross.
Die Kästchen mit Plus oder Minuszeichen sind feste Ladungen.
Die Kreise mit Plus oder Minuszeichen sind bewegliche Ladungen.

Der pn-Übergang eindimensional (2)

Ionisierte Dotierungsatome:

Feste Ladung

Elektrisches Feld
Raumladungszone

$\frac{d(\epsilon_H E)}{dx} = \rho = q(N_D^+-N_A^-+p-n)$

$E = \int \frac{q}{\epsilon_H} \cdot (N_D^+-N_A^-+p-n) \, \mathrm{d}x$

Diffusionsstrom
Driftstrom
Potenzial, Spannung

$U = \int E \, \mathrm{d}x$

Poisson-Gleichung: Eine vorhandene elektrische Ladung erzeugt ein elektrisches Feld.
Entlang eines elektrischen Feldes ensteht eine elektrische Spannung.

Differentialgleichungssystem

Poissongleichung: U, E

$\frac{d(\epsilon_H E)}{dx} = \rho = q(N_D^+-N_A^-+p-n)$

$\epsilon_H$ Permittivität des Halbleiters $\epsilon_{Si} =11.7· \epsilon_0$
$N_D^+$ Ionisierte Donatoren

Transportgleichung

$j_p = q\mu_p p \left(E - V_T \frac{1}{p}\frac{\delta p}{\delta x} \right)$

$j_n = q\mu_n n \left( E + V_T \frac{1}{n}\frac{\delta n}{\delta x} \right)$

Kontinuitätsgleichung

$\frac{\delta J_p}{\delta x} = - q \left(\frac{\delta p(x)}{\delta t}-G\right)$

$\frac{\delta J_n}{\delta x} = q \left(\frac{\delta n(x)}{\delta t}-G\right)$

Die Lösung dieser Gleichungen ergibt:Löcher- und Elektronendichte, Raumladungsdichte $\rho$ , Feldstärke E, Potenzial $\Psi$

Die Transportgleichung besteht aus dem Driftstrom und Diffusionsstrom.

Ausdehnung der Sperrschicht/Raumladungszone (RLZ)

Neutralitätsbedingung

$N_A·x_p = N_D·x_n$

Ausdehnung der Sperrschicht

$d_S = \sqrt{\frac{2 \epsilon_H U_D \left(N_A + N_D \right)}{q N_A N_D}}$

_H

Diffusionsspannung U_D (Built-in potential)
$U_D = \frac{kT}{q} ln\left(\frac{N_A N_D }{n_i^2} \right)$
Temperaturspanung $U_T = \frac{kT}{q}$
k: 1.38 · 10^-23J/K Boltzmannkonstante
Wie verhält sich die Sperrschicht und die Diffusionsspannung bei verschiedenen Dotierungskonzentrationen?

Beispiel: Diffusionsspannung und Sperrschicht einer Diode

Berechnen Sie die Diffusionsspannung und die Sperrschichtdicke (Raumladungszonendicke) einer Siliziumdiode mit N_A=1·10¹⁷cm^-3 und N_D=1·10²⁰cm^-3.

$\epsilon_{Si} =11.8· \epsilon_0 =11.8·8.85 ·10^{-14}Fcm^{-1}$

$q=1.6 ·10^{-19}C; kT/q=0.025V; n_i=1.5·10^{10}cm^{-3}$
MathNotepad

p-Typ Halbleiter Akzeptor:

$N_A=1·10^{17}cm^{-3}$
n-Typ Halbleiter Akzeptor:

$N_D=1·10^{20}cm^{-3}$

$U_D = \frac{kT}{q} ·ln\left(\frac{N_A N_D }{n_i^2}\right) = 0.025V ·ln\left(\frac{1·10^{17}cm^{-3}·1·10^{20}cm^{-3}}{1.5·1.5·10^{20}cm^{-6}}\right) = 0.958V$

$d_S = \sqrt{\frac{2 \epsilon_H U_D \left(N_A + N_D \right)}{q N_A N_D}} =0.112\mu m$

NA=1E17
ND=1E20
Esi=11.8*8.85E-14
UT=0.025
ni=1.5E10
UD=UT*log(NA*ND/ni^2)
q=1.6E-19
ds=sqrt(2*Esi*(NA+ND)*UD/q/NA/ND)

Raumladungszone mit äußerer Spannung

Sperrschichtweite, Raumladungszonenweite

$d_S = \sqrt{\frac{2 \epsilon_H \left( N_A + N_D \right) \left(U_D-U\right)}{q N_A N_D}}$

U äußere Diodenspannung

Größe: $U_D – U \gt 0$
Sperrrichtung (Spannung U negativ)
In der Raumladungszone kommt es zur thermischen Generation von Ladungsträgern, die vom äußeren elektrischen Feld abgesaugt werden.

Sehr kleiner Sperrstrom

Bei einer positiven externen Spannung U_D wird die Raumladungszonenweite 0.
Bei negativen Spannungen U < 0 V wird U_D - U größer und damit auch die Raumladungszone immer größer.
Bei einer Diodenspannung von U = 0 V bleibt die Diffusionsspannung übrig und erzeugt eine Raumladungszone.

Relevanz:
Bei einem realen Bauteil muss Platz für die Raumladungszone im Halbleiter vorhanden sein. Stößt die Raumladungszone an die Anschlüsse oder geometrischen Grenzen kann es zu einem Durchbruch, einem erhöhten Strom im Sperrbereich kommen.
Gerade bei kleinen Geometrieen im nm Bereich ist das eine Herausforderung.

Diode mit äußerer Spannung

Verteilung beweglicher Ladungsträger
Sperrrichtung

Die Raumladungszone wird größer
Es stehen keine beweglichen Ladungsträger in der Raumladungszone zur Verfügung
Kein Stromfluß

Durchlassrichtung

Die Anzahl beweglicher Ladungsträger erhöht sich.
Es fliesst ein Strom

<---- Diodenspannung ----
0 V

Strom-Spannungskennlinie der Diode

Vorwärtsbetrieb $I_D = I_S\left( e^{\frac{qU}{nkT}}-1\right)$

$\frac{U}{nU_T} \gt 1$

$I_D = I_S \left( e^{\frac{U}{nU_T}} \right)$

Temperaturspannung: $U_{T} = \frac{kT}{q} = 0.025 V$ für T=300K, Raumtemperatur
$10^{-18}A \lt I_S \lt 10^{-9}$
Schleusenspannung oder Flussspannung
Darstellungen

Achsen linear

Strombereich für positive und negative Werte unterschiedlich

Stromachse logarithmisch

Stromwerte absolut
Kein Logarithmus einer negativen Zahl möglich
Ablesen des Exponenten

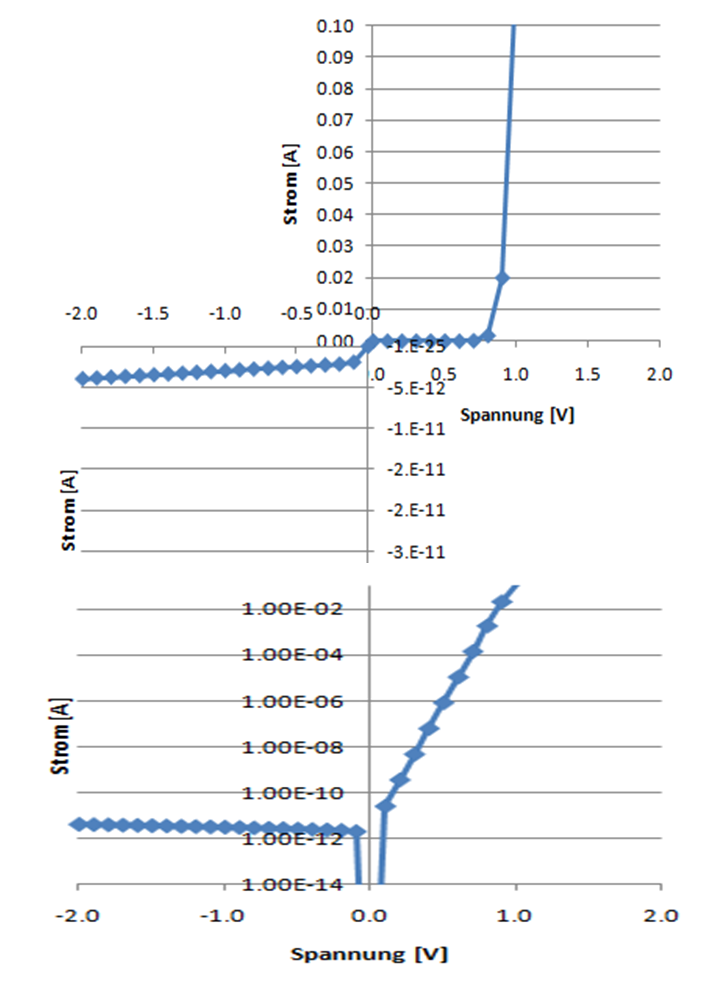Quelle: Vollrath

Rückblick

Differentialgleichungen

Poisson: U,E (n,p, N_A, N_D)
Transportgleichung: J_n,J_p, (E, dn/dx, dp/dx)
Kontinuitätsgleichung: dJ_n/dx, J_p/dx, (G, dn/dt, dp/dt)

Was ist eine Raumladungszone?
Welche Gleichungen werden benötigt um das Strom Spannungsverhalten eines Halbleiters zu beschreiben?
Wie lautet die Diodengleichung?
Wie wird die Weite der Raumladungszone d_S berechnet?
Diffusionsspannung: U_D
Temperaturspannung: $U_{T} = \frac{kT}{q} = 0.025 V$ für T=300K, Raumtemperatur

Kapazitäten

Sperrschichtkapazität
(Junction Capacitance)

C_S, C_J

$C_{j0}$ : Diodenkapazität bei 0V

$C_S = C_J = \frac{C_{J0}}{\sqrt{1-\frac{U}{U_D}}}$

Es bildet sich eine Raumladungszone mit festen Ladungsträgern.
Durch die äußere Spannung wird die Größe der Raumladungszone und damit die Kapazität verändert.
Dies wirkt wie ein Plattenkondensator.

Diffusionskapazität
Bei einem Stromfluss befindet sich ein Überschuss an Ladungsträger in der Diode. Bei Änderung der angelegten Spannung verändert sich dieser Ladungsträgerüberschuss.

$C_D = \frac{d(Q)}{dU} = \tau_D \frac{I}{U_T}$

τ_D: Transitzeit
U_{T: Temperaturspannung}

Schaltverhalten: Einschalten und Ausschalten

DiodeSchalt.asc

Version 4
SHEET 1 1356 680
WIRE 48 64 32 64
WIRE 128 64 48 64
WIRE 240 64 208 64
WIRE 256 64 240 64
WIRE 32 96 32 64
WIRE 256 96 256 64
WIRE 32 192 32 176
WIRE 144 192 32 192
WIRE 256 192 256 160
WIRE 256 192 144 192
WIRE 144 208 144 192
FLAG 144 208 0
FLAG 48 64 U1
FLAG 240 64 UD
SYMBOL voltage 32 80 R0
WINDOW 3 -50 169 Left 2
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR Value PULSE(-1.9 1.9 0.1u 1n 1n 0.05u 0.1u)
SYMATTR InstName V1
SYMBOL res 224 48 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R1
SYMATTR Value 100
SYMBOL diode 240 96 R0
SYMATTR InstName D1
SYMATTR Value 1N4148X
TEXT -24 280 Left 2 !.tran 0 0.18u 80n 0.00001u
TEXT -32 312 Left 2 !.model 1N4148X D(Is=2.52n Rs=.568 N=1.752 Cjo=4p M=.4 tt=40n \n+ Iave=200m Vpk=75 mfg=Motorola type=silicon)
TEXT -32 368 Left 2 !;dc V1 -3 3 0.1

SPICE Simulation
τ_d Aufladung der Diffusionskapazität
Stationärer Strom I₁

$\tau_S = \tau_D ln\left( 1- \frac{I_1}{I_2} \right)$
τ_S Speicherzeit: Entladung der Diffusionskapazität
t_f Abfallzeit t_f ~ C_S(R_V+R_B)

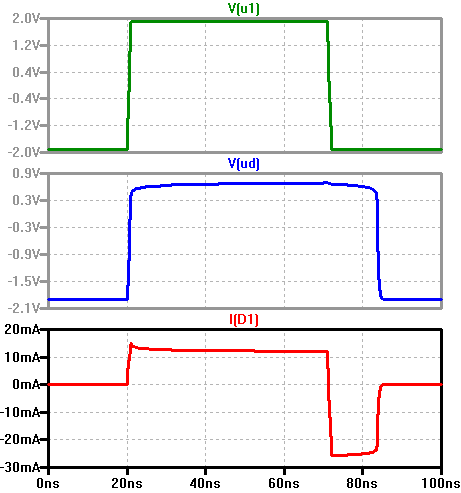td Stromspitze Einschalten, ts konstanter Gegenstrom, tf Abfall des Gegenstroms

Für positive Spannung U1 erwartet man einen Stromfluss (12 mA) und für negative Spannung U1 keinen Stromfluss, ein Sperrverhalten.
Beim Abschalten sieht man in der Simulation dennoch für eine gewisse Zeit (t_s) einen unerwünschten Sperrstrom (-25mA).

Man kann den Einfluss des Widerstandes R1, der Flussspannung/Flusstrom und der Sperrspannung auf die Stromspitze in Flussrichtung und den Sperrstrom, wie in der Gleichung für τ_S angegeben untersuchen.

Schaltverhalten: Messung

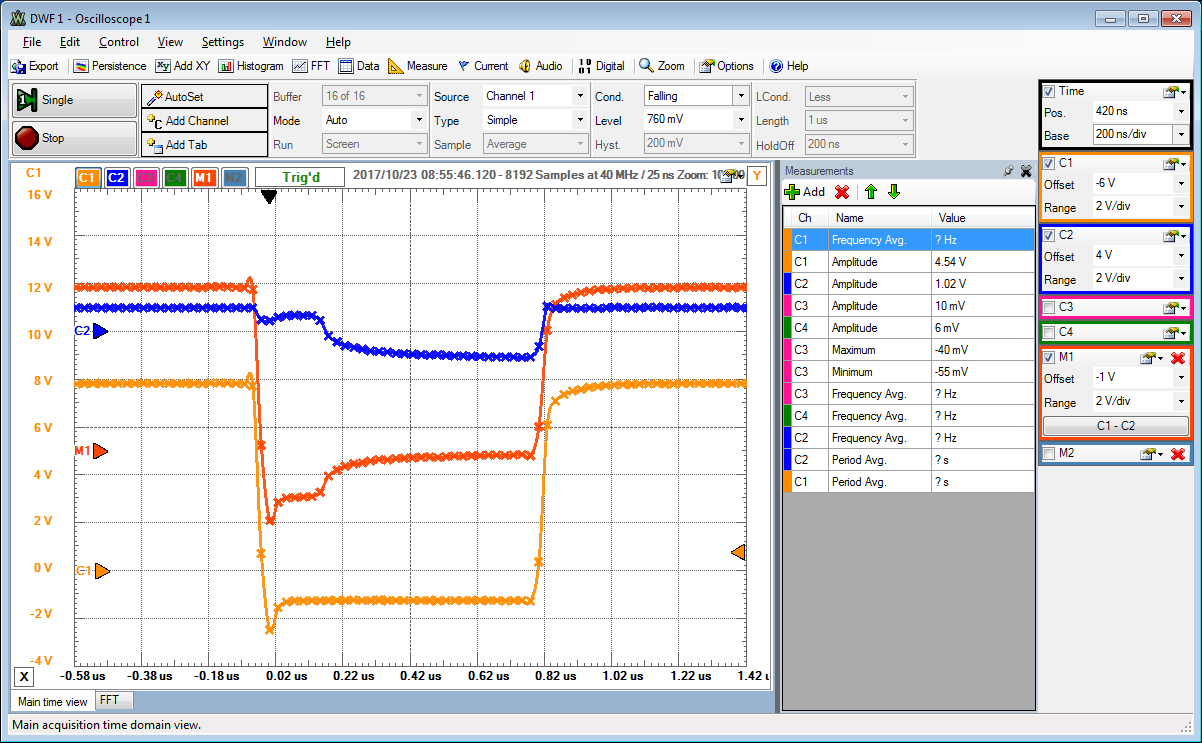
Mittlere Diode aus dem Diodenversuch.
Kleinster Widerstand 100 Ω am Ende des Sockels.
C1 zeigt das Rechteckeingansgsignal zwischen +8 V und -2 V mit einer Frequenz von 500kHz.
C2 zeigt die Diodenspannung.
Ohne eine Speicherladung im pn Übergang, sollte der Strom (M1) durch die Diode bei Sperrspannung sofort Null werden.
Da gespeicherte Ladung vorhanden ist, sieht man noch einen Stromfluss.
Dieses Verhalten entspricht einem Kapazitätsverhalten, man spricht von der Diffusionskapazität.

Nächstes Mal:

Rechnen Sie die Aufgabe Klausur WS2011: Aufgabe 1
Variationen der Aufgabe:
Es kann nach der Spannung oder der Dotierstoffkonzentration für eine bestimmte Raumladungszonengröße gefragt werden.

Diodenschaltung

05 Diode

2023 Elektronik 3 04 pn Übergang Prof. Dr. Joerg Vollrath