Interface Electronics

10/11 ADC Pipeline

Prof. Dr. Jörg Vollrath

09 ADC Architectures Flash and SAR

Video Lecture: pipeline ADC 16.12.2020

Länge:

0:0:10 Switched capcitor circuit

0:2:14 Pipeline ADC

0:3:12 3-bit Pipeline folding ADC

0:5:13 Residue transfer curve

0:8:30 Gray code

0:10:20 Benefits of pipeline ADC

0:15:40 Sample and hold circuits

0:17:4 Folding circuit

0:19:55 Regular pipeline ADC Example 2-bit per stage, 4-bit

0:21:55 Residue, transfer curve

0:26:0 Adding DAC and input voltage

0:29:40 Gain of 3

0:37:11 Transfer table

0:47:10 Circuit

0:48:2 Simulated curve

0:48:0 LTSPICE simulation with gain error

0:52:32 Staying inside the box

0:56:14 Input and residue signals

0:58:57 Simulation and calibration

1:4:33 ADC Error Simulation with pipeline ADC

1:6:48 Lower gain 1.8

1:11:27 Folding pipeline ADC

1:23:19 Simulation and calibration

1:16:54 1.5 Bits per stage

1:18:40 Scalable cyclic pipeline ADC

1:22:0 sample and hold to prevent frequency doubling

Review and Overview

Pipeline ADC basic idea
Practical Realisation 1 Bit per stage
A Folding Pipeline ADC

Outcome:

Realize challenges of amplifiers
Difficulty of range adjustment

Pipeline ADCs

Idea:

Use Residue for finer quantization.
ADC, DAC structure or folder.

Residue is the difference between the analog input signal and the digital output code.

A pipeline ADC

3-bit, one bit per stage, 3-stage folding pipeline ADC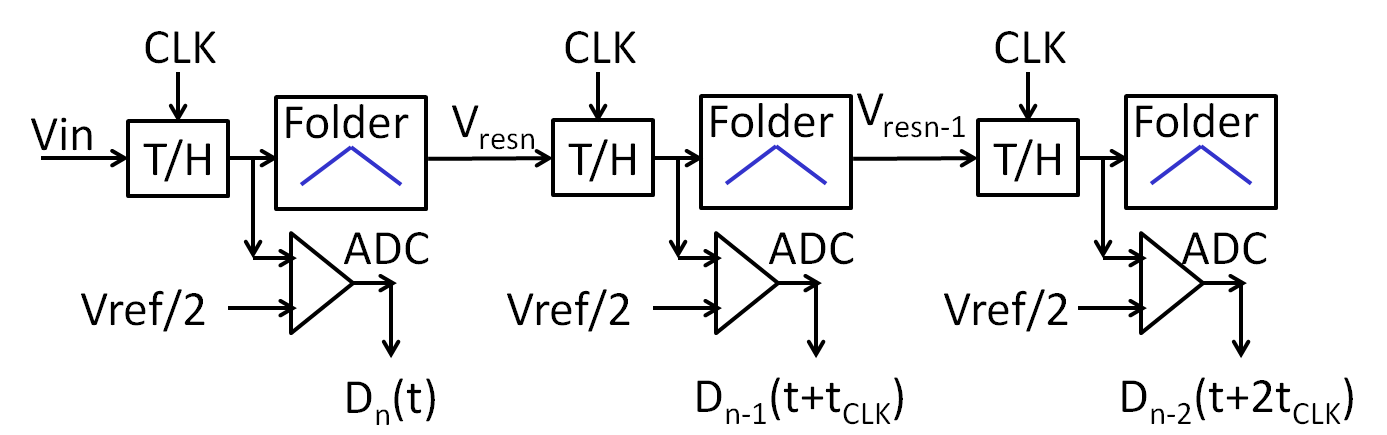

It takes B clock cycles to generate 3 B data bits.
The latency is B · t_CLK. Concurrent operation is possible and the sample rate is f_CLK.

Properties:
3 stages
Each stage has one sample and hold (T/H), one folder and one 1 bit ADC.
If the output range of the folder is the same as the input range, there is no redundancy or error correction. (1 bit per stage)
Offset and gain error of the folder will cause INL and DNL error and limit performance.
The output range should be a little smaller than the input range to be able to correct folder errors. (0.95 bit per stage)
This circuit needs all sample and hold otherwise the frequency of input voltage at each stage would double causing bandwidth problems.
Since the folding operation does not depend on the ADC high speed operation is possible.
The folder will cause nonlinearities, since the peak of the transfer function will be rounded.

It takes 3 (B) clock cycles to generate 3 (B) data bits.
Since each stage has a separate sample and hold concurrent operation is possible and the sample rate is f_CLK.
The latency is B · t_CLK.

Variations of the pipeline ADC can have:
- A residue generator instead of the folder requiring a DAC, a subtract stage and a gain stage.
- More than one bit per stage (multiple folding).

Folding pipeline ADC internal voltages

The output code is a Gray code.
A typical curve of input voltage, residue voltages and output code is shown below.

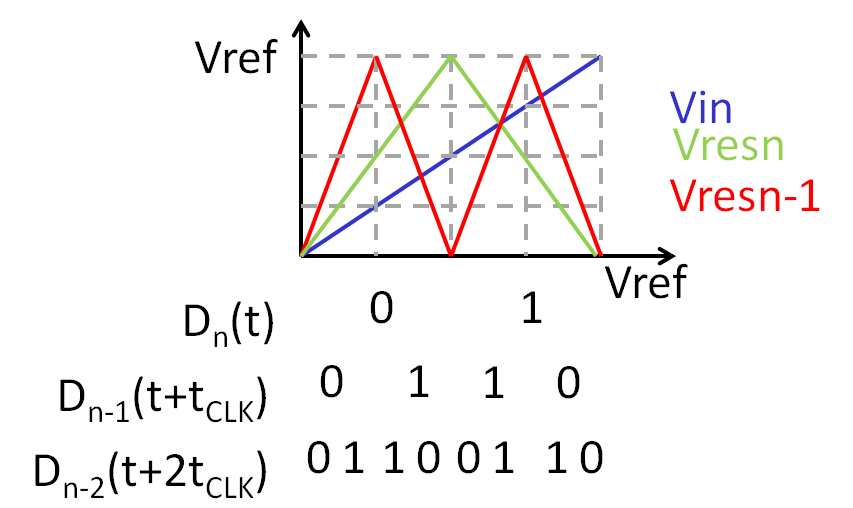
Example pipeline ADC internal voltages

Pipeline ADC with residue generator.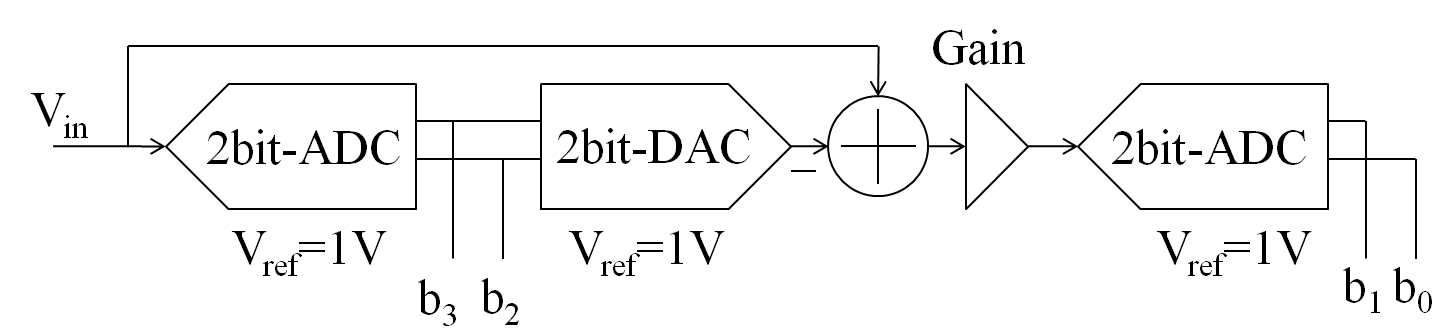

The input ADC has the first transition at 1 LSB instead of normally 1/2 LSB.
Calculate the input range for the b3, b2 codes.
Make a table for the transfer function for a gain of 4 and a gain of 3.

First determine the minimum voltage where b3b2 are changing:
0.25 Vref, 0.5 Vref and 0.75 Vref
For each subrange calculate the residue after the gain stage.
V_res = (Vin - (b3b2)*0.25) * gain
Minimum voltage where b1b0 are changing:
Vres = 0.25 Vref, 0.5 Vref and 0.75 Vref
For each combination b3b2b1b0 Vin can be calculated:
Vin = b3b2 * 0.25 (0.25 * (b1b0) * Vref) / gain
Gain = 4
The second stage sees Vres between 0..1 V at the 2-bit ADC voltage.
b1b0 are also changing at 0.25 Vref, 0.5 Vref and 0.75 Vref
Transfering this to the input means dividing the voltage by the gain:
0.0625 V, 0.125 V, 0.1875 V
Now the table can be filled:

Code b3b2b1b0	Nr	Vinmin(Gain=4) [Vref]
0000	0	---
0001	1	0 + 0.0625
0010	2	0 + 0.125
0011	3	0 + 0.1875
0100	4	0.25
0101	5	0.25 + 0.0625
0110	6	0.25 + 0.125
0111	7	0.25 + 0.1875
1000	8	0.5
1001	9	0.5 + 0.0625
1010	10	0.5 + 0.125
1011	11	0.5 + 0.1875
1100	12	0.75
1101	13	0.75 + 0.0625
1110	14	0.75 + 0.125
1111	15	0.75 + 0.1875

The transfer curve will be limited and cut off at 0V and Vref.

Practical Opamp Realisation with 1 Bit per stage

PipeStage_t.asc

Version 4
SHEET 1 880 680
WIRE 304 32 288 32
WIRE 416 32 384 32
WIRE 624 32 496 32
WIRE 144 48 144 32
WIRE 144 48 -32 48
WIRE 560 64 560 16
WIRE 416 80 416 32
WIRE 528 80 416 80
WIRE 144 96 144 48
WIRE 624 96 624 32
WIRE 624 96 592 96
WIRE 656 96 624 96
WIRE -272 112 -272 96
WIRE -144 112 -144 96
WIRE 112 112 16 112
WIRE 368 112 304 112
WIRE 480 112 448 112
WIRE 528 112 480 112
WIRE 16 128 16 112
WIRE 16 128 -32 128
WIRE 240 128 240 32
WIRE 240 128 176 128
WIRE 256 128 240 128
WIRE 480 128 480 112
WIRE -32 144 -32 128
WIRE 112 144 80 144
WIRE 256 144 256 128
WIRE 80 192 80 144
WIRE 304 192 304 112
WIRE 304 192 80 192
WIRE 560 192 560 128
WIRE 144 224 144 160
WIRE 144 224 -32 224
WIRE 288 224 288 32
WIRE 288 224 256 224
WIRE 480 224 480 208
WIRE 256 240 256 224
WIRE 144 256 144 224
WIRE -272 304 -272 288
WIRE 256 336 256 320
FLAG 144 32 VDDp
FLAG 144 256 VDDn
FLAG 80 144 In
IOPIN 80 144 In
FLAG 656 96 Vout
IOPIN 656 96 Out
FLAG 560 192 VDDn
FLAG 560 16 VDDp
FLAG 480 224 0
FLAG 256 336 0
FLAG 240 32 Dout
IOPIN 240 32 Out
FLAG -144 112 0
FLAG -272 112 0
FLAG -272 16 VDDp
FLAG -144 16 VDDn
FLAG -272 304 0
FLAG -272 208 IN
SYMBOL res -48 32 R0
SYMATTR InstName R1
SYMATTR Value 10k
SYMBOL res -48 128 R0
SYMATTR InstName R2
SYMATTR Value 10k
SYMBOL res 464 112 R0
SYMATTR InstName R3
SYMATTR Value 200k
SYMBOL res 464 96 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R4
SYMATTR Value 100k
SYMBOL res 512 16 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R5
SYMATTR Value 200k
SYMBOL res 400 16 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName R6
SYMATTR Value 100k
SYMBOL res 240 224 R0
SYMATTR InstName R7
SYMATTR Value 100
SYMBOL res 240 128 R0
SYMATTR InstName R8
SYMATTR Value 100
SYMBOL voltage -272 0 R0
SYMATTR InstName V1
SYMATTR Value 4.5
SYMBOL voltage -144 0 R0
SYMATTR InstName V2
SYMATTR Value -3
SYMBOL voltage -272 192 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V3
SYMATTR Value SINE(0 5 1k)
SYMBOL Opamp3 144 128 R0
WINDOW 0 8 -72 Bottom 2
SYMATTR InstName X3
SYMATTR SpiceLine Aol=100000 GBW=0.01G
SYMBOL Opamp3 560 96 R0
WINDOW 0 8 -72 Bottom 2
SYMATTR InstName X1
SYMATTR SpiceLine Aol=100000 GBW=0.01G
TEXT -296 352 Left 2 !.dc V3 -4.5 4.5 0.02
TEXT -304 -96 Left 2 !.global VDDp VDDn

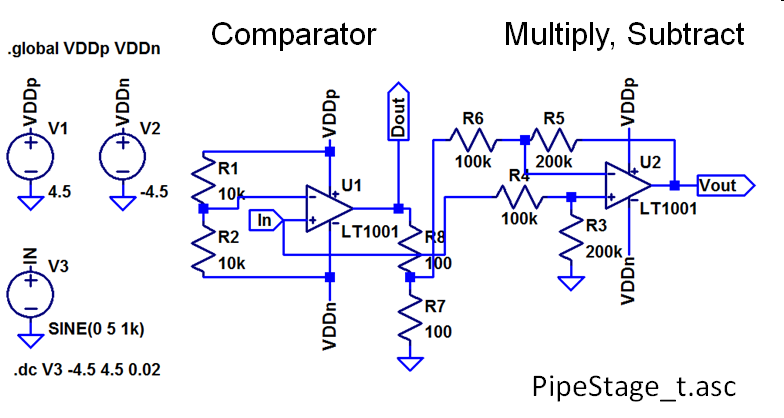
V_out = 2 ( V_in - 0.5 D_out)

On the left the comparator is shown, on the right the folding and amplification stage.
Accuracy is limited by generating the correct level after the comparator and having the right gain at the multiply and add stage. Speed is limited by the critical path from small input difference change of comparator to full level swing of the output to generate residue.

Practical Realisation Simulation Output

Comparison of ideal case and gain error. (Picture on the right)
Comparison of ideal case and offset error.

Discussion:
Clipping of output (red circles) limits the resolution of the ADC. (R7=150 Ω)
There is a dead zone at the center of the curve.
No code change will happen in the dead zone defining and limiting LSB.
Reduction of output reduces the input range.(R7=70 Ω)

Offset error (RE=1000kΩ) will give missing codes. (Next slide)

PipeStage5Bit.asc

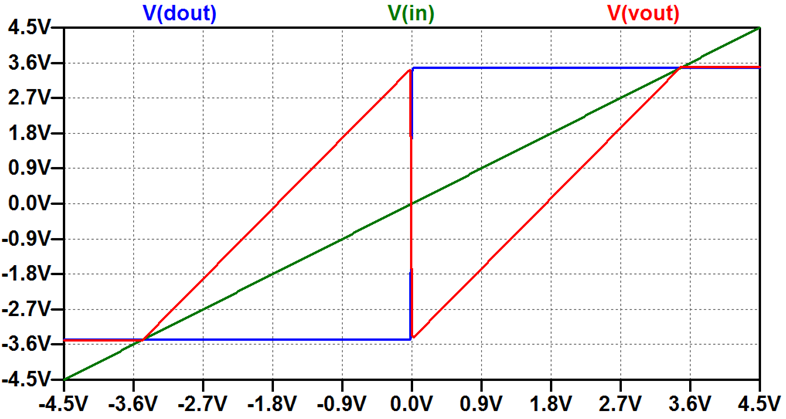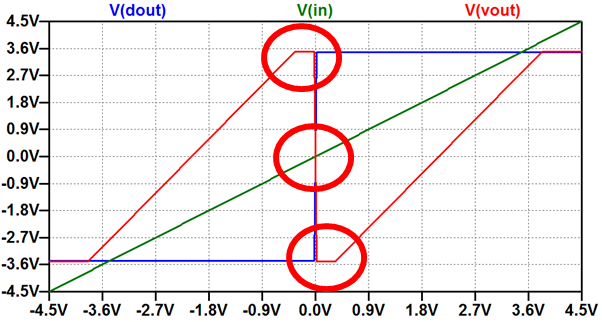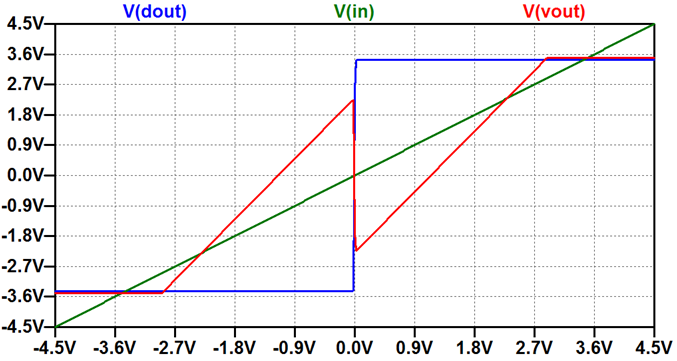Staying Inside the Box 1

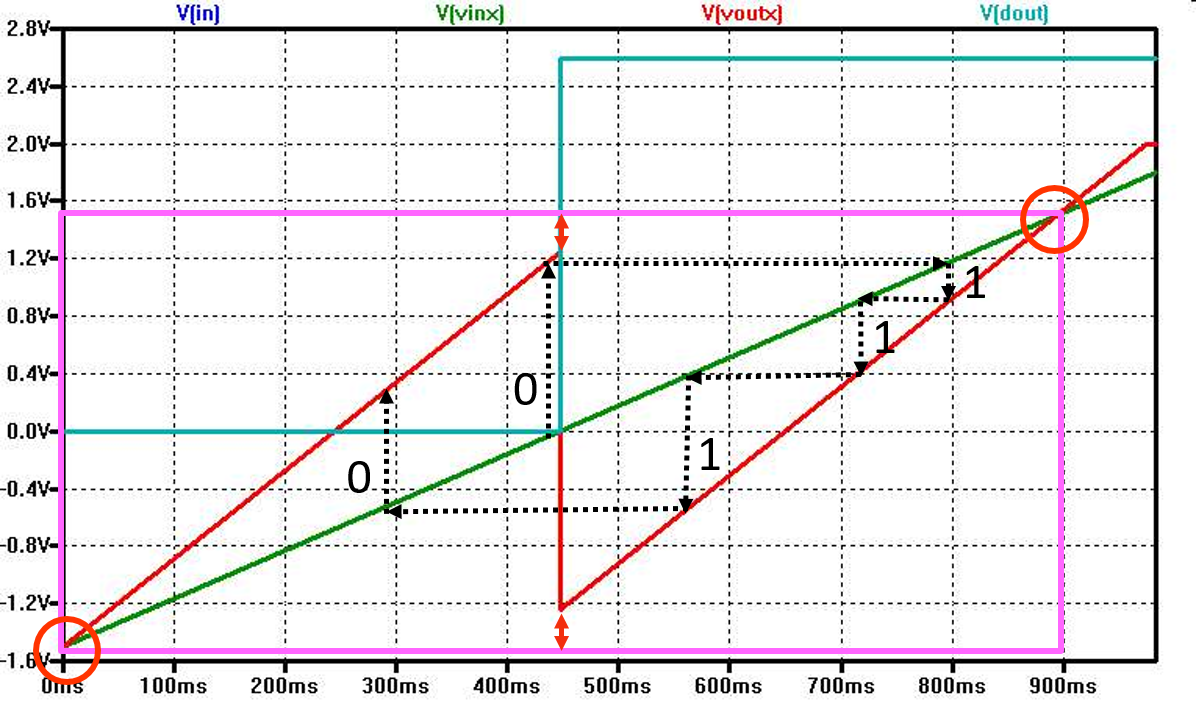
The pink rectangle shows the operation range of the pipeline ADC.
The rectangle is defined by crossing of V(vin) = V(vinx) and Vres (V(voutx)).
For an input voltage close to mid level the code 01111 or 10000 is expected.
Looking at the graph dashed arrows show the operation.
Since the gain of the stage is lower than expected a mid level voltage is not mapped to a maximum Vres (01111) or a minimum Vres (1000).
Following the dashed arrows a code of 01110 is generated.
Code 01111 will not be generated and is missing.

Staying Inside the Box 2

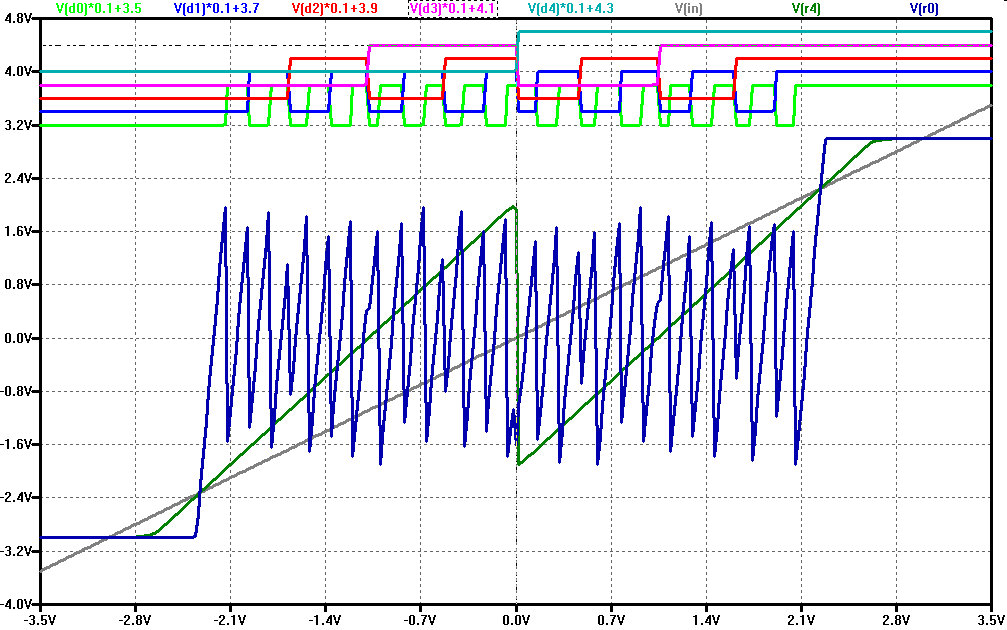
The residue of the 5th stage has varying maxima and minima.
The frequency of the signal at the 5th stage would be 32 times higher than the input ramp frequency.
To limit the maximum frequency sample and holds between stages are used.
Matching of input and output range is very important and difficult.

Simulation and Calibration of a pipeline ADC

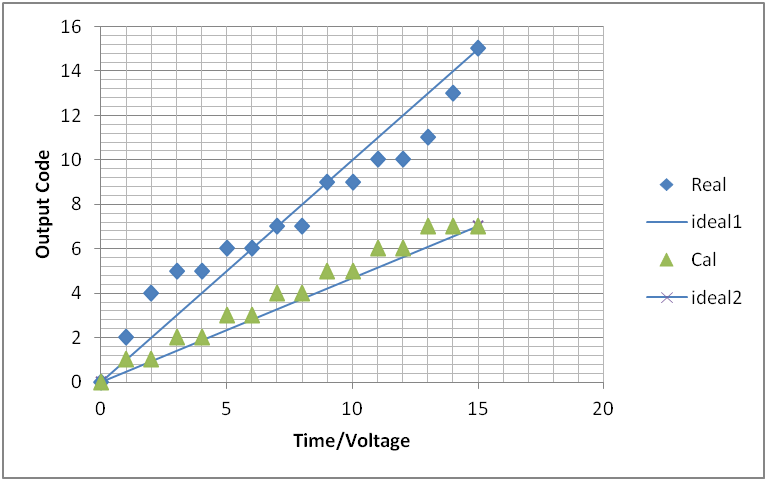
ADC Simulation
4 bit pipeline ADC
Gain Error 2.1
Gain Error 1.9

Typical output codes:
Missing output codes: gain low and has margin.
Changing slope of transfer characteristic: amplifier non linear

Calibration: Condense codes and use lowest slope.
FFT and ADC Calibration

Simulation and Calibration of a pipeline ADC

4-bit gain 1.7 nonlinear folding pipeline ADC:

Folding function: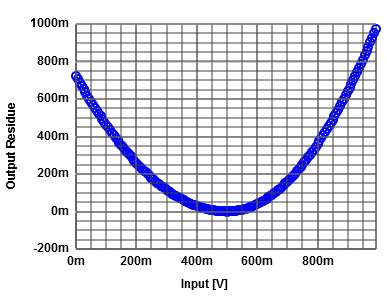	Transfer function: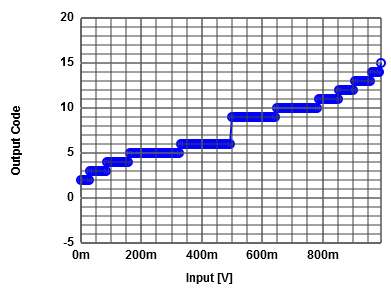	FFT: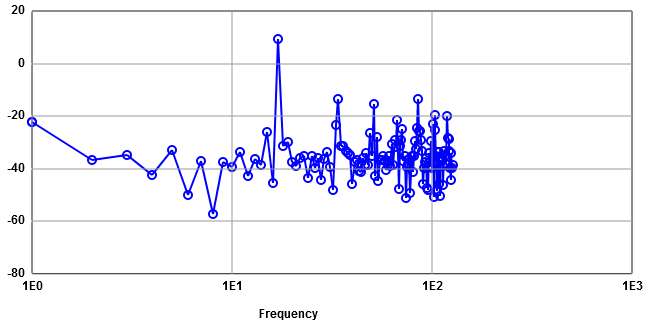
ENOB: (16.08 dB - 1.76 dB)/6.02 dB = 2.38 Calibration: ENOB: (16.5 dB - 1.76 dB)/6.02 dB = 2.44	Calibration: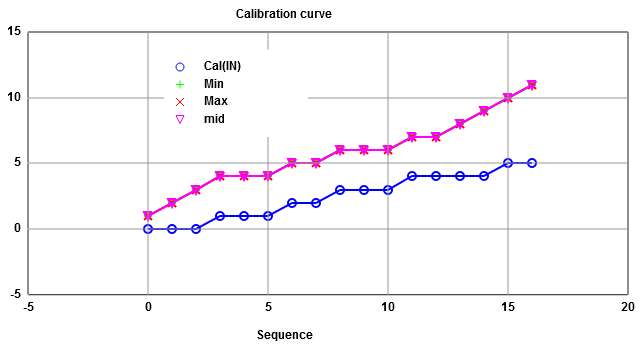	FFT: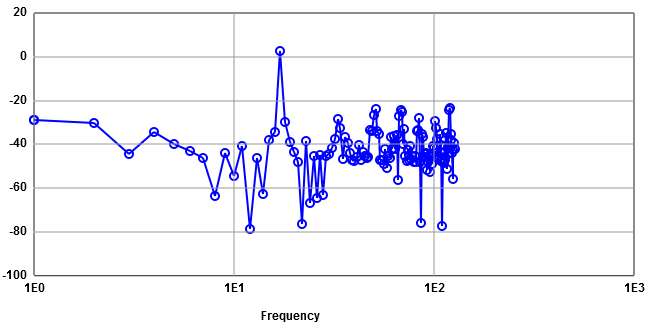

Calibration helps to overcome missing codes and non linearities.
Details of simulation:
Signal 9.34 dB Noise -6.73 dB
1st Harmonic -13.56 dB Only noise -15 dB

Calibration:
Signal 2.6 dB Noise -13.9 dB
1st Harmonic -23.62 dB Only noise -20 dB

Gain 1.7 nonlinear folding pipeline ADC:
8-bit: 33.14 dB - 17.09 dB = 16.05 dB
8-bit calibrated: 13.86 dB - (- 12.19 dB) = 26.05 dB
10-bit: 45.45 dB - (29.16 dB) = 16.3 dB
10-bit cal: 13.99 dB - (-13.34 dB) = 27.33 dB

1.58 bit stage for a pipeline ADC

There are 3 codes possible:
00,01,11

ld(3) = 1.58 bits

Scalable cyclic pipeline ADC

BlockFoldingPipeline.asc

Version 4
SHEET 1 1368 680
WIRE 96 304 64 304
WIRE 64 320 64 304
WIRE 624 336 80 336
WIRE 352 352 320 352
WIRE 352 384 352 352
WIRE 208 400 176 400
WIRE 304 400 272 400
WIRE 336 400 304 400
WIRE 416 400 368 400
WIRE 528 400 416 400
WIRE 32 416 0 416
WIRE 416 416 416 400
WIRE 624 416 624 336
WIRE 624 416 592 416
WIRE 32 432 32 416
WIRE 528 432 512 432
WIRE 16 448 -16 448
WIRE 48 448 48 336
WIRE 96 448 48 448
WIRE 112 448 96 448
WIRE 176 448 176 400
WIRE 176 448 112 448
WIRE 96 464 96 448
WIRE 416 496 416 480
WIRE 512 496 512 432
WIRE 624 496 512 496
WIRE 624 512 624 496
WIRE 176 528 176 448
WIRE 256 528 176 528
WIRE 96 544 96 528
WIRE 368 544 320 544
WIRE 624 608 624 592
FLAG 368 544 Ds0
IOPIN 368 544 Out
FLAG -16 448 A
IOPIN -16 448 In
FLAG 96 544 0
FLAG 0 416 CLK1
FLAG 304 400 res0
FLAG 112 448 sample0
FLAG 416 496 0
FLAG 320 352 CLK2
FLAG 416 400 sample1
FLAG 96 304 CLK3
FLAG 624 608 0
SYMBOL SampleHold 32 448 R0
SYMATTR InstName X1
SYMBOL cap 80 464 R0
WINDOW 0 22 8 Left 2
SYMATTR InstName C1
SYMATTR Value 4.7p
SYMBOL Comparator 288 528 R0
SYMATTR InstName X2
SYMBOL Folder 240 400 R0
SYMATTR InstName X3
SYMBOL SampleHold 352 400 R0
SYMATTR InstName X4
SYMBOL cap 400 416 R0
SYMATTR InstName C2
SYMATTR Value 4.7p
SYMBOL SampleHold 64 336 M0
SYMATTR InstName X5
SYMBOL res 608 400 R0
SYMATTR InstName R1
SYMATTR Value 100k
SYMBOL res 608 496 R0
SYMATTR InstName R2
SYMATTR Value 100k
SYMBOL Opamp1 560 416 R0
SYMATTR InstName X6
TEXT 704 232 Left 2 !.include cmosedu_models.txt\n.global vdd\nV1 Ax 0 SINE(0.466 0.06 0.0005G) AC 1\nVDD VDD 0 DC 1\nVA A 0 PULSE(0.35 0.6 0 10u 10u 0 20u)\n*VA A 0 PULSE(0.35 0.585 0 1000u 1000u 0 2000u)\nVCLK1 CLK1 0 DC 0\nVCLK2 CLK2 0 DC 0\nVCLK3 CLK3 0 DC 1\n*VCLK1 Clk1 0 PULSE(1 0 0 0.1n 0.1n 19.9n 800n)\n*VCLK2 CLK2 0 PULSE(1 0 25n 0.1n 0.1n 19.9n 80n)\n*VCLK3 CLK3 0 PULSE(1 0 50n 0.1n 0.1n 19.9n 80n)\n.tran 0 40u 0 0.1n\n* .dc VA 0 1 0.0001\n* .noise v(Y) VA dec 10 10 10G

With CLK1 an external voltage is sampled to C1.
CLK2 active samples the residue on the capacitor C2.
Activating CLK3 afterwards generates the next data and the next residue.
This operation is repeated until the desired number of bits is reached.
Then another external sample is taken via CLK1.
In this architecture sampling speed and resolution can be traded.

Summary

Repetive pipeline process
High bandwidth, N_Bit latency
Supply voltage limit
Folder, operational amplifier gain, offset, linearity error
Error correction
Algorithmic, lookup table

Example: WS2013 Problem 1

References

Low transistor count pipeline ADC example

Non linear pipeline ADC investigation

Lewis et. al., "A 10-b 20-Msample/s analog-to-digital converter," JSSC 3/1992
D. W. Cline, P.R Gray, "A power optimized 13-b 5 MSamples/s pipelined analog-to-digital converter in 1.2um CMOS," JSSC 3/1996
E. G. Soenen et al., "An architecture and an algorithm for fully digital correction of monolithic pipelined ADCs," TCAS II, pp. 143-153, March 1995
A. N. Karanicolas et al. "A 15-b 1-Msample/s digitally self-calibrated pipeline ADC," IEEE J. of Solid-State Circuits, pp. 1207-15, Dec. 1993
L. Singer et al., "A 12 b 65 MSample/s CMOS ADC with 82 dB SFDR at 120 MHz," ISSCC 2000, Digest of Tech. Papers., pp. 38-9

12 Sigma Delta ADC

2023 09 29 Interface Electronics 10 ADC Pipeline Prof. Dr. Joerg Vollrath

Interface Electronics

10/11 ADC Pipeline

Prof. Dr. Jörg Vollrath

Video Lecture: pipeline ADC 16.12.2020

Review and Overview

Outcome:

Pipeline ADCs

A pipeline ADC

Folding pipeline ADC internal voltages

Example pipeline ADC internal voltages

Practical Opamp Realisation with 1 Bit per stage

Practical Realisation Simulation Output

Staying Inside the Box 1

Staying Inside the Box 2

Simulation and Calibration of a pipeline ADC

Simulation and Calibration of a pipeline ADC

1.58 bit stage for a pipeline ADC

Scalable cyclic pipeline ADC

Summary

References