Elektronik 3

13 Digitaltechnik

Prof. Dr.

Jörg Vollrath

12 Schaltregler

Video Digitaltechnik Transistorrealisierung
Video Digitaltechnik Logische Verknüpfung
Video Verzögerungszeiten

Digitaltechnik

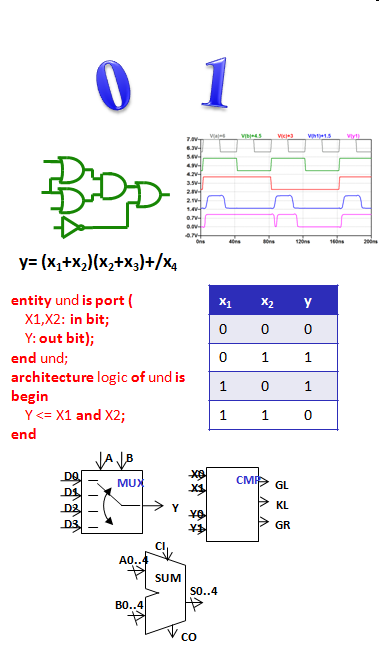CMOS Transistoren als Schalter

	Symbol	Eingang: Gate
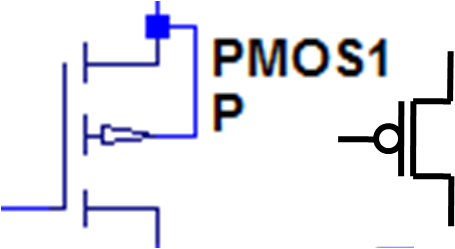
PFET Transistor: Eingang 1: Schalter offen Eingang 0: Schalter geschlossen Logikschaltung: PFETs im Schaltplan oben, verbunden mit VDD		0	1
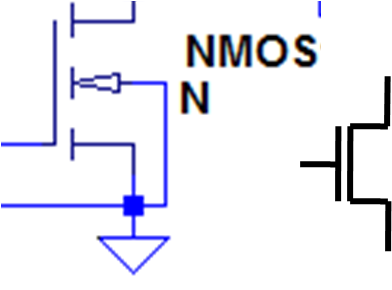
NFET Transistor: Eingang 1: Schalter geschlossen Eingang 0: Schalter offen Logikschaltung: NFETs im Schaltplan unten, verbunden mit GND, VSS, 0V.		0	1

Zur Realisierung von booleschen Funktionen werden MOSFET (metal oxide semiconductor field effect transistor) Transistoren eingesetzt.
Dabei werden Halbleiter (semiconductor, Silizium) verwendet, bei denen man durch Einbringen von Femdatomen (Dotierung) die Leitfähigkeit (Elektronen, Löcher) verändern kann.
Der MOS Transistor hat drei Anschlüsse Gate, Drain und Source.
Das Gate ist der Eingang. An der Drain ist der Ausgang und an der Source ist VDD (Betriebsspannnung, PFET) oder GND (0 V, NFET).
FET Feldeffekttransistor ist der Überbegriff für Halbleiterbaulemente, bei denen das elektrische Feld zwischen Gate und Kanal den Kanalwiderstand steuert bzw die Verbindung zwischen Drain und Source trennt oder schliesst.
Es gibt PFETs (PMOSFETs, Löcherleitung, positive Ladungsträger, Löcher) und NFETs (NMOSFETs, negative Ladungsträger, Elektronen) deren Verhalten komplementär sind (complementary metal oxide semiconductors, CMOS).
Ist die Gatesourcespannung beim NFET positiv, größer als eine Schwellspannung (threshold voltage), wird die Verbindung zwischen Drain und Source leitend (Ein Schalter wird geschlossen).
Ist die Gatesourcespannung beim PFET negativ, kleiner als eine Schwellspannung, wird die Verbindung zwischen Drain und Source leitend (Ein Schalter wird geschlossen).
Durch geschicktes Kombinieren der Transistoren können Logikfunktionen technisch realisiert werden.
Fast alle modernen Mikroprozessoren und digitalen Schaltungen werden mit CMOS Transistoren realisiert.

CMOS Inverter (NOT) als Transistorschaltung

Inv_Trans.asc

Version 4
SHEET 1 1008 680
WIRE 560 -48 560 -64
WIRE 560 -48 224 -48
WIRE 608 -48 560 -48
WIRE 608 0 608 -48
WIRE 608 0 560 0
WIRE 512 48 512 32
WIRE 512 48 432 48
WIRE 384 112 336 112
WIRE 432 112 432 48
WIRE 432 112 384 112
WIRE 560 112 560 48
WIRE 656 112 560 112
WIRE 224 160 224 -48
WIRE 336 160 336 112
WIRE 560 160 560 112
WIRE 592 208 560 208
WIRE 432 240 432 112
WIRE 512 240 432 240
WIRE 224 272 224 240
WIRE 336 272 336 240
WIRE 336 272 224 272
WIRE 560 272 560 256
WIRE 560 272 336 272
WIRE 592 272 592 208
WIRE 592 272 560 272
WIRE 560 288 560 272
FLAG 560 288 0
FLAG 560 -64 VDD
FLAG 656 112 OUT
IOPIN 656 112 Out
FLAG 384 112 In
SYMBOL pmos4 512 -48 R0
SYMATTR InstName M5
SYMATTR Value P
SYMATTR Value2 l=0.05u w=0.23u
SYMBOL nmos4 512 160 R0
SYMATTR InstName M6
SYMATTR Value N
SYMATTR Value2 l=0.05u w=0.1u
SYMBOL voltage 336 144 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName Vin
SYMATTR Value 0.5
SYMBOL voltage 224 144 R0
SYMATTR InstName V2
SYMATTR Value 1.0
TEXT 200 -96 Left 2 !.include cmosedu_models.txt
TEXT 216 304 Left 2 !.dc Vin 0 1 0.01

Der Schaltplan zeigt einen Inverter, eine Nicht (NOT) Funktion.
Nach der Wahrheitstabelle soll bei einer '1' am Eingang eine '0' am Ausgang erscheinen.
Das Signal wird invertiert.
Jeder Logikschaltkreis benötigt eine Spannungsversorgung (VDD).
Früher wurde für die Darstellung der '1' 5 V verwendet. Mit der Verkleinerung der Transistoren wurde die Geometrie kleiner. Damit die auftretenden elektrischen Feldstärken gleich blieben, wurde auch die Versorgungsspannung verkleinert.
2018 arbeitet man mit Versorgungsspannungen um die 1 V.
Dieser Pegel wird auch für die Logiksimulation verwendet. Im Praktikum sind Bausteine im Einsatz, die eine Versorgungsspannung zwischen 2.5 V und 5 V benötigen.

CMOS Inverter (NOT) Funktionalität

PFET, NFET
Eingang1 -> Ausgang 0

Kein Stromfluss von VDD nach GND

Input 0 -> Output 1

No current from VDD to GND

Transition Region

High current flow

VDD = 1.0V
Eingang: V_IH > 0.6V, V_IL < 0.4V
Ausgang: V_OH > 0.7V, V_OL < 0.3V
Ideale Kurve: rot
Reale Kurve: blau
Strom: grün

In der Simulation wird die Kennlinie eines Inverters dargestellt. Bei der Simulation wird am Eingang die Spannung V_in von 0 auf 1 V verändert und die Ausgangsspannung beobachtet.
Die Ausgangsspannung V_out ändert sich um V_in = 0.5 V von 1 V auf 0 V.
Man sieht in Grün, dass der Strom bei 0.5 V maximal ist. Bei 0 V und 1 V Eingangsspannung fließt fast kein Strom.
In Rot ist noch die Idealkennlinie eines Inverters dargestellt. Die reale Kennlinie ist sehr nah an der idealen Kennlinie.
Da um 0.5 V ein digitales Ergebnis nicht klar definiert ist, spezifiziert man mindest Eingangspegel V_I und Ausgangspegel V_O (output) für '0' low (L) und '1' high (H), mit denen das digitale System korrekt arbeitet.

Physikalische Realisierung: CMOS Layout

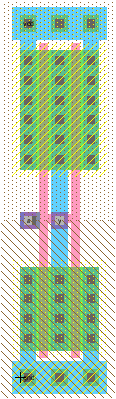
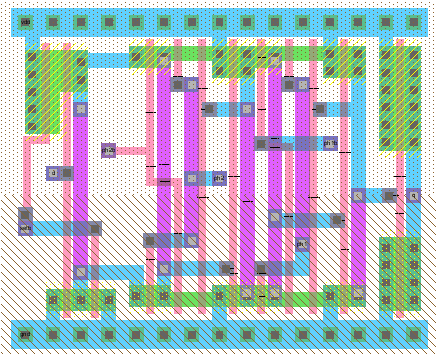
In integrierten Schaltungen werden Transistoren durch Strukturierung von verschiedenen Lagen von Materialien durch phototechnische Schritte erzeugt.
Die Strukturen für die Realisierung werden dabei in einem Layout festgelegt.
Unterschiedlich farbige Flächen stehen für unterschiedliche Materialien in unterschiedlichen übereinanderliegenden Ebenen.
Im Beispiel sind blaue und violette Flächen Metallverbindungen meist aus Aluminium.
Schwarze und graue Punkte sind Verbindungen (Kontakte) zwischen verschiedenen Ebenen.
Kreuzungen zwischen grünen Flächen und orangenen Linien erzeugen Transistoren.
Ist der Hintergrund punktiert entsteht ein PFET, ist der Hintergrund liniert ein NFET.
Einfache Strukturen werden nebeneinander gelegt und ergeben komplexere Funktionen, bis hin zum rechts gezeigten Mikroprozessor.
Typische Strukturgrößen reichen von früher einigen µm bis 2018 einigen nm.

Bsp: Bestimmung einer Schaltfunktion

NAND2a.asc

Version 4
SHEET 1 880 680
WIRE 336 -48 272 -48
WIRE 352 -48 336 -48
WIRE 432 -48 352 -48
WIRE 496 -48 432 -48
WIRE 352 0 352 -48
WIRE 352 0 272 0
WIRE 496 0 496 -48
WIRE 496 0 432 0
WIRE 208 32 176 32
WIRE 224 32 208 32
WIRE 384 32 352 32
WIRE 272 64 272 48
WIRE 352 64 272 64
WIRE 432 64 432 48
WIRE 432 64 352 64
WIRE 496 64 432 64
WIRE 352 96 352 64
WIRE 416 144 352 144
WIRE 208 176 208 32
WIRE 304 176 208 176
WIRE 416 240 416 144
WIRE 416 240 352 240
WIRE 304 272 272 272
WIRE 416 288 416 240
WIRE 416 288 352 288
WIRE 416 304 416 288
FLAG 416 304 0
FLAG 336 -48 VDD
FLAG 496 64 Y
IOPIN 496 64 Out
FLAG 176 32 A
IOPIN 176 32 In
FLAG 272 272 B
IOPIN 272 272 In
FLAG 352 32 B
IOPIN 352 32 In
SYMBOL nmos4 304 192 R0
SYMATTR InstName M1
SYMATTR Value N
SYMATTR Value2 l=0.05u w=0.1u
SYMBOL nmos4 304 96 R0
SYMATTR InstName M2
SYMATTR Value N
SYMATTR Value2 l=0.05u w=0.1u
SYMBOL pmos4 384 -48 R0
SYMATTR InstName M3
SYMATTR Value P
SYMATTR Value2 l=0.05u w=0.1u
SYMBOL pmos4 224 -48 R0
SYMATTR InstName M4
SYMATTR Value P
SYMATTR Value2 l=0.05u w=0.10u

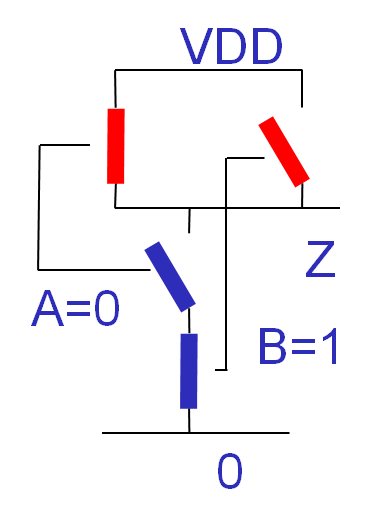
Die Transistoren werden im ersten Schritt durch Schalter ersetzt.
Bei einer gewählten Eingangssignalkombination wird dann verfolgt, ob der Ausgang mit VDD oder GND (0 V) verbunden ist, und sich so eine '1' oder '0' ergibt.
Daraus ergibt sich dann eine Wahrheitstabelle.

Darstellung boolescher Verknüpfungen NAND

Schaltfunktion

Y = f(X1,X2) = /(X1 ^ X2) = !(X1 · X2)
X1, X2: Eingangsvariablen
Y: Ausgangsvariable
^: Operationssymbol

Schaltzeichen, Schaltsymbol

Wahrheitstabelle

X1	X2	Y
0	0	1
0	1	1
1	0	1
1	1	0

Textuelle VHDL Beschreibung


entity NAND is port (
    X1,X2: in bit;
    Y: out bit);
end NAND;
architecture logic of NAND is
begin
    Y <= NOT(X1 and X2);
end

Boolesche Algebra Grundfunktionen

Schaltfunktion

Schaltsymbol

Wahrheitstabelle

NICHT, NOT

\( Y = \overline{X} = !X = /X \)
Y <= not (X);
Y = !X;

x	Y
0	1
1	0

Der Kreis markiert die Invertierung des Signals.
Zur vereinfachten Darstellung kann statt eines Inverters ein Kreis am Eingang gezeichnet werden.

Boolesche Algebra Grundfunktionen

Schaltfunktion

Schaltsymbol

Wahrheitstabelle

UND, AND

Y = X1 ^ X2 = X1 · X2
Y <= X1 and X2;
y = X1 && X2;

X1	X2	Y
0	0	0
0	1	0
1	0	0
1	1	1

ODER, OR

Y = X1 v X2 = X1 + X2
Y <= X1 or X2;
y = X1 || X2;

X1	X2	Y
0	0	0
0	1	1
1	0	1
1	1	1

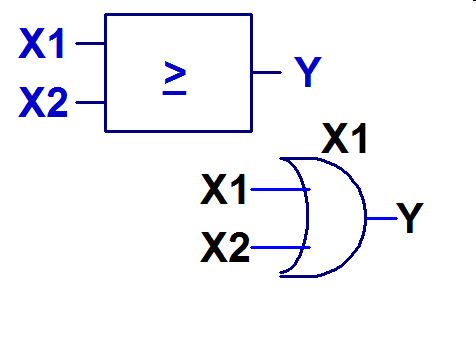
Diese Grundfunktionen finden sich in Formelsammlungen wieder oder werden auswendig gelernt.
Die Namen entsprechen der erwartenden Funktion (sprechende Namen).
UND: Nur wenn Eingang X1 und Eingang X2 '1' sind ergibt sich am Ausgang eine '1'.
ODER: Immer wenn Eingang X1 oder Eingang X2 '1' ist ergibt sich am Ausgang eine '1'.

Boolesche Algebra Grundfunktionen

Schaltfunktion

Schaltsymbol

Wahrheitstabelle

NAND

\( Y = \overline{X1 \wedge X2} \)
\( Y = \overline{X1 · X2} \)
Y <= not (X1 and X2);
y = not(X1 && X2);

X1	X2	Y
0	0	1
0	1	1
1	0	1
1	1	0

NOR

\( Y = \overline{X1 \vee X2} \)
\( Y = \overline{X1 + X2} \)
Y <= not( X1 or X2);
y = not( X1 || X2);

X1	X2	Y
0	0	1
0	1	0
1	0	0
1	1	0

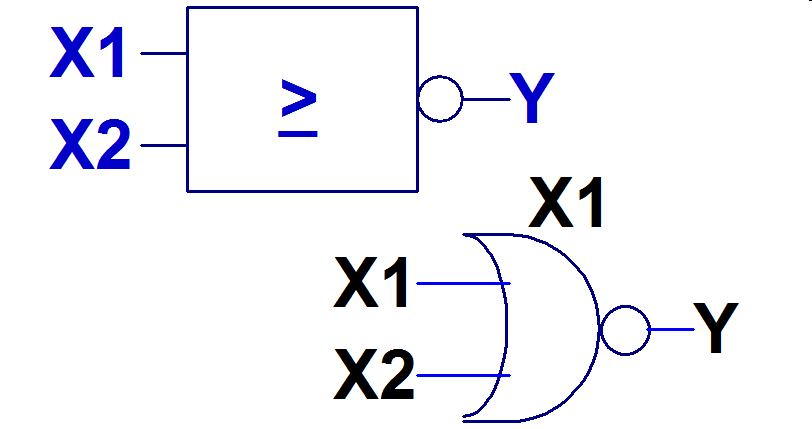
Das vorgestellte N steht für not oder nicht. Das Ausgangssignal der UND oder ODER Funktion wird invertiert.

Weitere Grundfunktionen

EXOR, XOR

Wahrheitstabelle

y=(not(X1) and X2) or (X1 and not(X2))
y=not(X1 and X2) and (X1 or X2)
Y= X1 xor X2;

X1	X2	Y
0	0	0
0	1	1
1	0	1
1	1	0

Boolesche Funktionen Wikipedia
Logikgatter Wikipedia

Logikfunktionen

Logikfunktionen in Excel

Simulation und Messung boolescher Verknüpfungen

Boolesche Algebra

Genauso wie für die Rechenregeln und Gesetze für natürliche Zahlen gibt es Rechenregeln und Gesetze für die boolesche Algebra.

Mehr Eingänge

Physikalische Realisierung

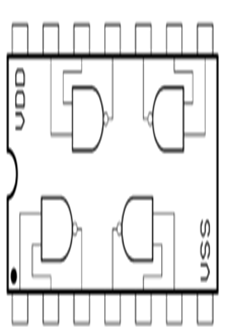
7400 4-fach NAND mit 2 Eingängen (Dual in line DIL14 Gehäuse)

Logiktransistorarray 4007

4007 Transistorarray	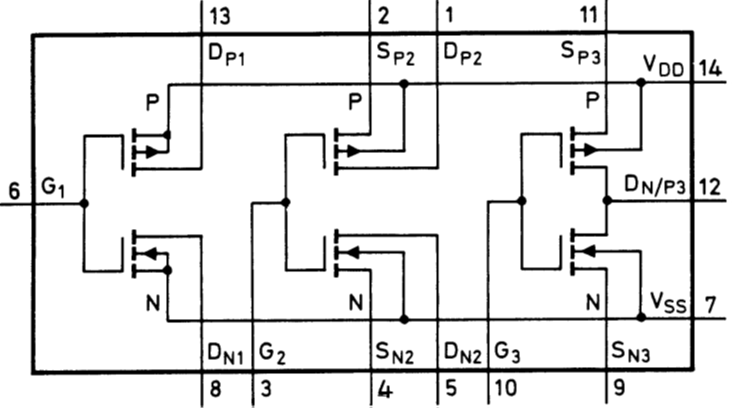4007 Transistorarray
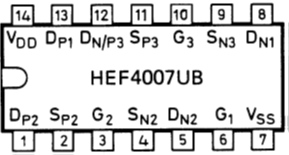4007 Transistorarray	NAND Gatter

Darstellung von NICHT, UND, ODER durch NAND Funktionen

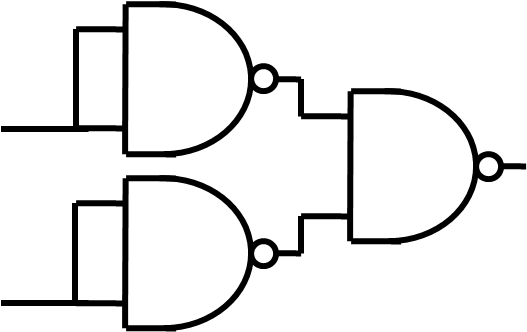
NICHT: Inverter	ODER
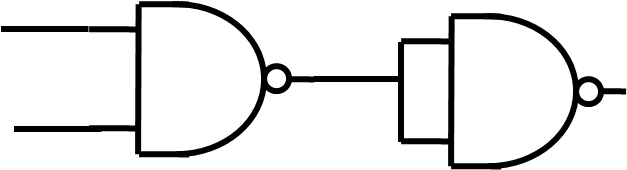
UND

Der Beweis der Äquivalenz ergibt sich entweder durch Vergleich der Wahrheitstabellen oder durch Umformung der Gleichung mit der booleschen Algebra.
NAND: y = /(x1 · x2)
NICHT: /x = /(x · x)
UND: x1 · x2 = /(/(x1 · x2))
ODER: x1 + x2 = /(/x1 · /x2)

x1	x2	NICHT(X1) /x1	NICHT(X2) /x2	NAND / (x1 · x2)	UND x1 · x2	ODER x1 + x2	NOR /x1 · /x2
0	0	1	1	1	0	0	1
0	1	1	0	1	0	1	0
1	0	0	1	1	0	1	0
1	1	0	0	0	1	1	0

Verzögerungszeit

Propagation delay

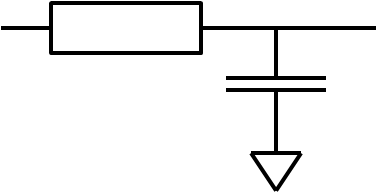
Vorstellung in der Elektrotechnik: Aufladung eines Kondensators (RC Delay)
Propagation Delay t_P: Blaue Pfeile Unterschiedlich für fallende und steigende Signale (Flanken) Unterschiedliche Transistoren sind aktiv.

Beispiel

NAND2_Sim.asc

Version 4
SHEET 1 880 680
WIRE 192 112 128 112
WIRE 32 128 32 112
WIRE 320 144 256 144
WIRE -80 160 -96 160
WIRE 192 160 128 160
WIRE -80 176 -80 160
WIRE 32 224 32 208
WIRE -80 272 -80 256
WIRE -64 272 -80 272
WIRE -64 288 -64 272
FLAG 128 112 A
FLAG 128 160 B
FLAG 320 144 Y
FLAG -64 288 0
FLAG 32 224 0
FLAG -96 160 A
FLAG 32 112 B
SYMBOL NAND2a 224 144 R0
SYMATTR InstName X1
SYMBOL voltage -80 160 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V1
SYMATTR Value PULSE(0 1 100n 1n 1n 99n 200n)
SYMBOL voltage 32 112 R0
WINDOW 123 0 0 Left 2
WINDOW 39 0 0 Left 2
SYMATTR InstName V2
SYMATTR Value PULSE(0 1 50n 1n 1n 49n 100n)
TEXT -136 72 Left 2 !.include cmosedu_models.txt
TEXT 32 288 Left 2 !.tran 200n
TEXT -240 112 Left 2 !VDD VDD 0 DC 1\n.global VDD

Definition

Die Zeit wird von der Änderung des Eingangssignals zur Änderung des Ausgangssignals gemessen.
Eine Lastkapazität (Eingangskapazität C der nächsten Logikschaltung) wird durch einen Transitor mit einem Kanalwiderstand R_DSon aufgeladen.

Bezugspegel zur Messung der Zeit sind 50% der Versorgungsspannung (Logisch '1').
Die Verzögerungszeit kann je nach steigender (PFET) oder fallender (NFET) Flanke des Signals am Ausgang variieren.
Die Verzögerungszeit kann bei verschiedenen Musterwechseln am Eingang unterschiedlich sein.
t_pdLH= t₂ - t₁; Der Ausgang geht von Low (0) auf High (1)
t_pdHL= t₄ - t₃; Der Ausgang geht von High (1) auf Low (0)

Ursache

Jeder CMOS Transistor hat eine Eingangskapazität am isolierten Gate und einen Widerstand zwischen Drain und Source.
Über den Widerstand wird die Eingangskapazität des nächsten Gatters aufgeladen oder entladen.
Dies benötigt etwas Zeit.

Zusammenfassung und nächste Vorlesung

Transistorrealisierung der boolschen Grundfunktionen

Nächstes Mal

14 Logische Verknüpfungen

2023 13 Digitaltechnik Elektronik 3 Prof. Dr. Joerg Vollrath

Elektronik 3

13 Digitaltechnik

Prof. Dr.

Jörg Vollrath

Digitaltechnik

CMOS Transistoren als Schalter

CMOS Inverter (NOT) als Transistorschaltung

CMOS Inverter (NOT) Funktionalität

Physikalische Realisierung: CMOS Layout

Bsp: Bestimmung einer Schaltfunktion

Darstellung boolescher Verknüpfungen NAND

Schaltfunktion

Schaltzeichen, Schaltsymbol

Wahrheitstabelle

Textuelle VHDL Beschreibung

Boolesche Algebra Grundfunktionen

Schaltfunktion

Schaltsymbol

Wahrheitstabelle

NICHT, NOT

Boolesche Algebra Grundfunktionen

Schaltfunktion

Schaltsymbol

Wahrheitstabelle

UND, AND

ODER, OR

Boolesche Algebra Grundfunktionen

Schaltfunktion

Schaltsymbol

Wahrheitstabelle

NAND

NOR

Weitere Grundfunktionen

EXOR, XOR

Wahrheitstabelle

Logikfunktionen

Logikfunktionen in Excel

Simulation und Messung boolescher Verknüpfungen

Boolesche Algebra

Mehr Eingänge

Physikalische Realisierung

Logiktransistorarray 4007

Darstellung von NICHT, UND, ODER durch NAND Funktionen

Verzögerungszeit

Beispiel

Definition

Ursache

Zusammenfassung und nächste Vorlesung