Komplexe Systeme werden aus einfachen Schaltungen erzeugt
Man sucht erst schnell überhaupt eine Lösung und
optimiert nur, wenn es Probleme (Funktionalität, Geschwindigkeit,
Leistungsverbrauch) gibt.
Alle Schaltungen müssen zur Sicherstellung der Funktionalität getestet werden.
Schaltungen sollen skalierbar und wiederverwendbar entworfen werden
EDA (Electronic Design Automation) Werkzeuge
helfen bei der Realisierung digitaler Systeme
AOI design style
NAND
\( Y = \overline{ X1 \cdot X2 \cdot X3} \)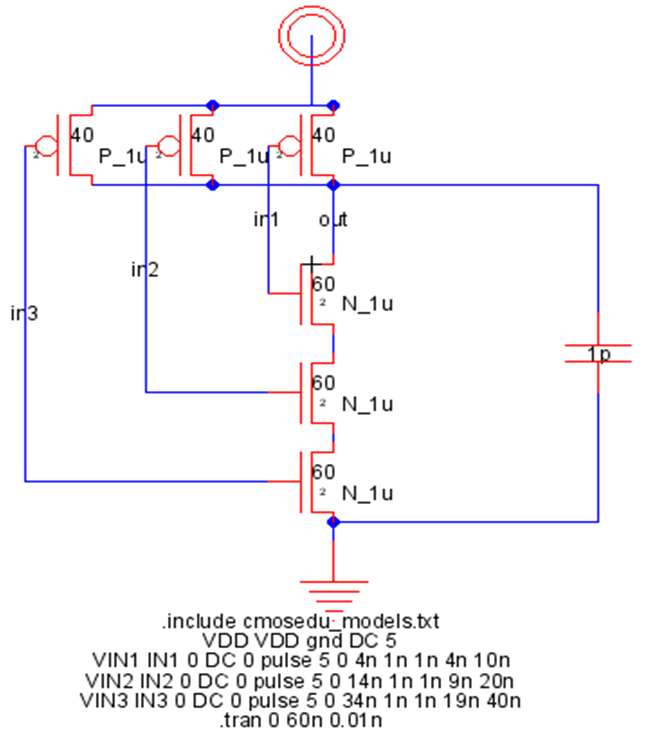
NOR
\( Y = \overline{ X1 + X2 + X3} \)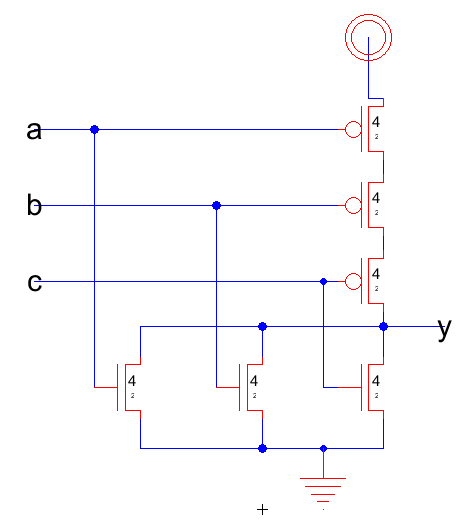
PFETs connected to VDD are at the top and NFET connected to GND at the bottom.
A NAND has PFETs on the top in parallel and NFETS at the bottom in series.
A NOR has PFETs on the top in series and NFETS at the bottom in parallel.
This can be used for arbitrary functions.
There can be additional inverters added to the inputs or outputs
to realize a logic function.
AOI design style example
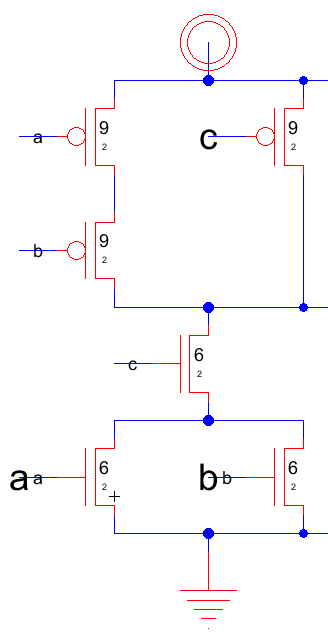
\( Y = \overline{ (a + b) \cdot c} \)
A
B
C
Y
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
1
1
0
1
0
1
1
0
1
1
1
1
0
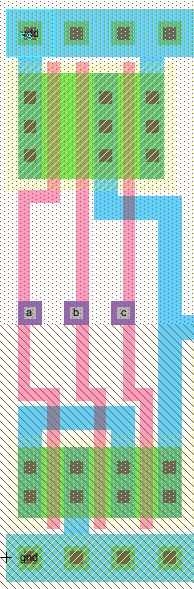Man sieht die Parallelschaltung der NFETs mit a und b als Eingang und
der PFET Reihenschaltung zur Realisierung
der NOR Verknüpfung /(a+b).
Zusammen mit dem NFET mit Eingang c in Reihe und PFET mit Eingang c parallel
ergibt sich die gewünschte Funktion y = /((a+b)c).
Von einer Problemstellung zu einer logischen Schaltung
Problemstellung: Eingänge und Ausgänge
Wahrheitstabelle
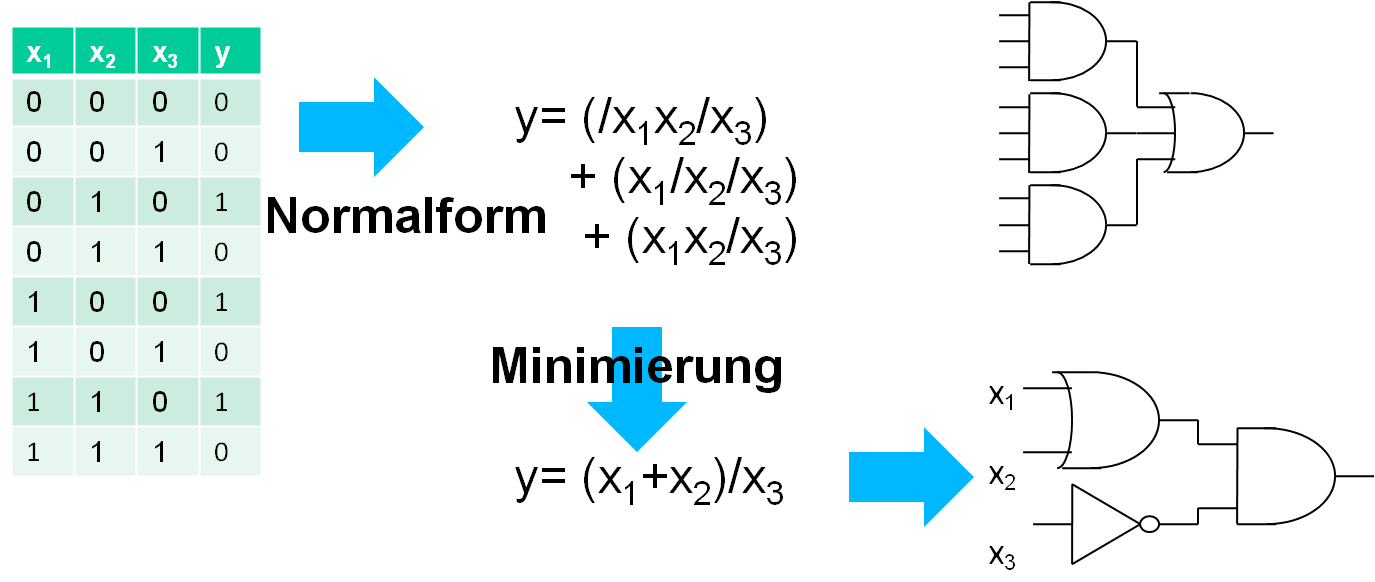
Ziel:
Realisierung der logischen Funktion mit möglichst wenig logischen Verknüpfungen:
Normalform, Minimierung
Für jede '1' am Ausgang y in einer Zeile der Wahrheitstabelle bestimmt man
die UND Verküpfung der Eingänge oder der invertierten Eingänge.
x1
x2
x3
y
0
1
0
1
y(010) = /x1 x2 /x3
Diese Gleichungen werden dann mit einer ODER Funktion verknüpft und ergeben
die Gleichung für die Wahrheitstabelle.
Logische Gleichung für eine Wahrheitstabelle
Normalform, disjunktive Normalform
Minimierung:
Boolesche Algebra
Karnaugh Veitch Diagramm
Algorithmisch (FPGA, VHDL Compilier)
Karnaugh Veitch Diagramm
Eine andere Darstellung einer Wahrheitstabelle
Nr
X Y Z
F
Minterm
0
0 0 0
1
/X/Y/Z
1
0 0 1
0
2
0 1 0
0
3
0 1 1
1
/XYZ
4
1 0 0
1
X/Y/Z
5
1 0 1
0
6
1 1 0
0
7
1 1 1
1
XYZ
Z
/Z
Y
3
7
6
2
1
5
4
0
/Y
/X
X
/X
Z
/Z
Y
1
1
0
0
0
0
1
1
/Y
/X
X
/X
Minimierung:
Zusammenfassung von horizontalen oder vertikalen Gruppen von 2,4 oder 8 '1'
Dabei kann man von rechts nach links über die Begrenzung des Kastens gehen.
Dabei kann man von oben nach unten über die Begrenzung des Kastens gehen.
In der linken Darstellung sind die Zeilen der Wahrheitstabelle angegeben in der man nach dem
Ausgangssignal suchen muss.
Darstellung eines Minterms durch NAND Funktionen
SOP-Ausdruck (sum of products)
(AB)+(CD)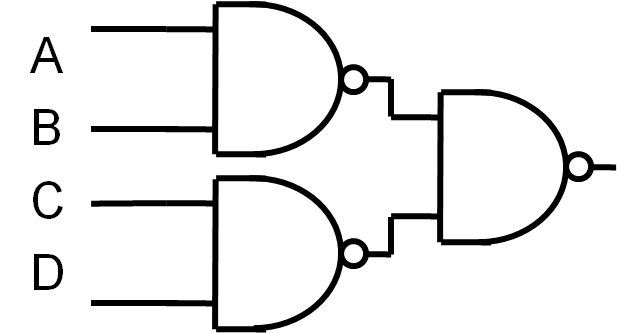
Verifikation mit einer Wahrheitstabelle
Zur Erstellung der Wahrheitstabelle werden die
Hilfssignale H1 = /(AB) und H2 = /(CD) eingeführt.
Die Hilfssignal erleichetern die Auswertung der logischen Funktionen.
A
B
C
D
H1=/(AB)
H2=/(CD)
SOP=/(H1H2)
(AB)
(CD)
(AB)+(CD)
0
0
0
0
1
1
0
0
0
0
0
0
0
1
1
1
0
0
0
0
0
0
1
0
1
1
0
0
0
0
0
0
1
1
1
0
1
0
1
1
0
1
0
0
1
1
0
0
0
0
0
1
0
1
1
1
0
0
0
0
0
1
1
0
1
1
0
0
0
0
0
1
1
1
1
0
1
0
1
1
1
0
0
0
1
1
0
0
0
0
1
0
0
1
1
1
0
0
0
0
1
0
1
0
1
1
0
0
0
0
1
0
1
1
1
0
1
0
1
1
1
1
0
0
0
1
1
1
0
1
1
1
0
1
0
1
1
1
0
1
1
1
1
0
0
1
1
1
0
1
1
1
1
1
0
0
1
1
1
1
Man sieht, dass die Spalten SOP und (AB)+(CD) gleich sind.
Für eine Messung muss man die Signale A, B, C und D erzeugen.
Dazu erzeugt man Pulse mit T (D), 2T (C), 4T (B) und 8T (A) Periodendauer.
Eine zeitliche Abfolge der Zeilen der Wahrheitstabelle innerhalb von 8T findet statt.
Schaltung zur Realisierung der Normalform
Stellen Sie die Wahrheitstabelle auf.
Geben Sie die logische Gleichung an.
Jedes Gatter hat eine Verzögerungszeit von 5 ns.
Geben Sie die maximale Verzögerungszeit an.
Wenn man den zeitlichen Verlauf der Signale zeichnen möchte,
sollte man erst alle Zwischensignale mit der berücksichtigten
Verzögerungszeit (5ns, Verschiebung der Änderung nach rechts) zeichnen.
Dabei Addieren sich Verzögerungszeiten auf:
Das Signal IN0 wird invertiert und steht mit 5ns Verzögerung als X3 zur Verfgung.
Nach dem ersten NAND Gatter ist die Verzögerungszeit von X4 zu IN0 dann (10ns = 5ns + 5 ns).
Out0 steht dann bei einer Änderung von IN0 aktualisiert nach 15ns (INV, NAND, NAND: 5 ns + 5 ns + 5 ns) zur Verfügung.
Da es kein Signal gibt mit mehr Logikschaltungen (Gattern) zwischen Eingang und Ausgang spricht man
vom längsten Pfad mit der maximalen Verzögerungszeit von 15 ns.
Durch die Verzögerungszeit kann es zu Glitchen (kurzen Signaländerungen) am Ausgang kommen.
Um diese am Ausgang zu vermeiden und Zustandsmaschinen zu bauen werden am
Ausgang Speicherelemente (Register) mit einer Taktsteuerung eingeführt.
Schaltung zur Realisierung der Normalform
Stellen Sie die Wahrheitstabelle auf.
Geben Sie die logische Gleichung an.
Jedes Gatter hat eine Verzögerungszeit von 5 ns.
Zeichnen Sie das Zeitverhalten, wenn die Wahrheitstabelle abgeprüft wird.
Geben Sie die maximale Verzögerungszeit an.
Eingänge
Signale
Ausgänge
IN2
IN1
IN0
X1
X2
X3
X4
X6
X7
X8
OUT0
OUT1
0
0
0
1
1
1
1
1
1
1
0
0
0
0
1
1
1
0
1
1
1
1
0
0
0
1
0
1
0
1
1
1
0
1
0
1
0
1
1
1
0
0
1
0
1
0
1
1
1
0
0
0
1
1
0
1
1
1
1
0
1
0
1
0
1
0
1
1
1
1
0
0
1
1
0
0
0
1
1
1
1
1
0
0
1
1
1
0
0
0
1
1
1
1
0
0
Geben Sie die logische Gleichung für Out0 an:
OUT0 = (IN2 /IN1 /IN3) + (/IN2 IN1 IN0)
Geben Sie die logische Gleichung für Out1 an:
OUT1 = (/IN2 IN1/IN0) + (/IN2 IN1 IN0)
Die maximale Verzögerungszeit beträgt 3 * 5 ns = 15 ns.
Ein NAND Gatter hat nur dann eine 0 am Ausgang, wenn alle Eingänge auf 1 sind.
X4 ist nur dann 0, wenn IN2=1, /IN1=1 und /IN0=1 ist.
Eine ähnliche Schaltung wird im
Versuch 2 realisiert.
